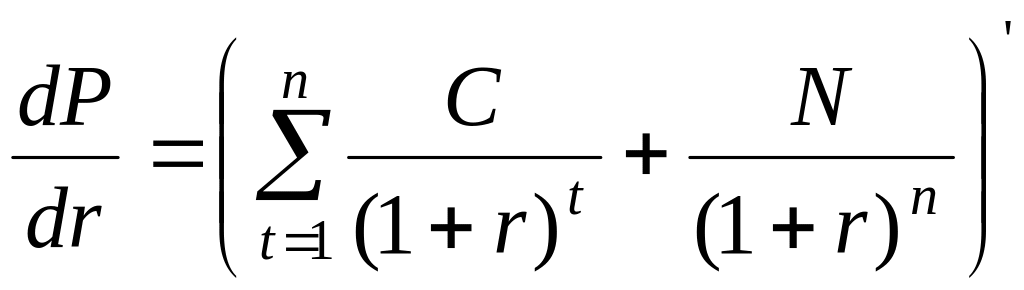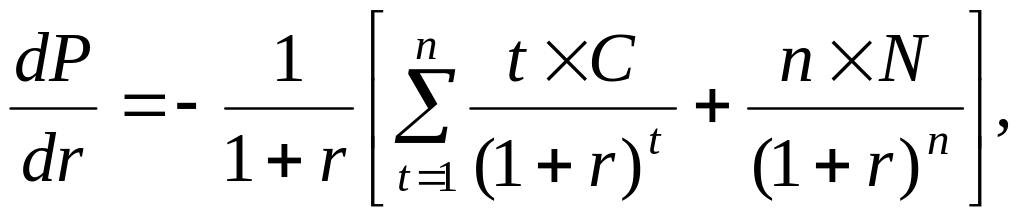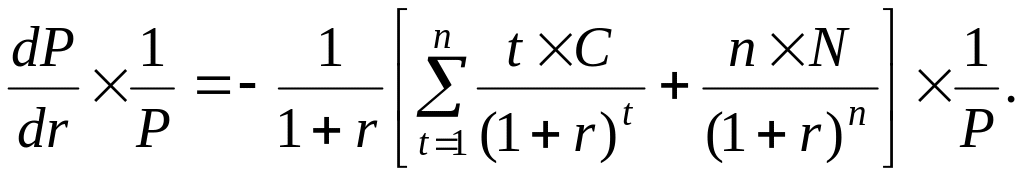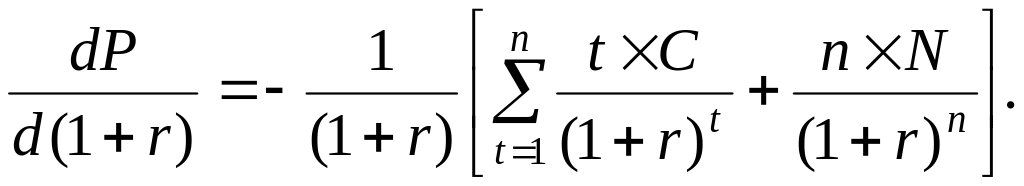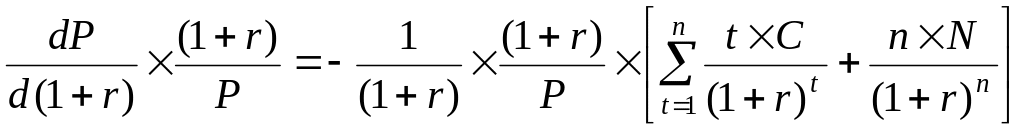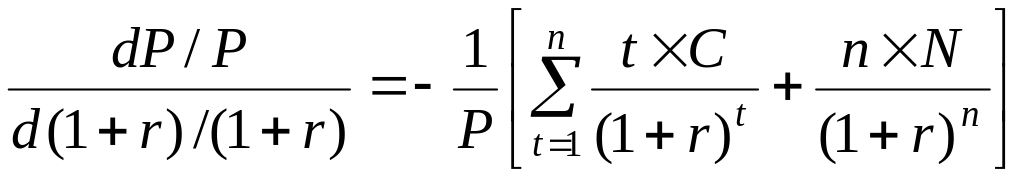2.1.4. Определение цены и доходности облигации с учетом налоговых и комиссионных платежей

До настоящего момента мы определяли значения цены и доходности облигаций, не учитывая тот факт, что по ним могут взиматься налоги и выплачиваться комиссионные вознаграждения брокерским компаниям.

Данные поправки легко сделать, скорректировав соответствующим образом формулы определения цены и доходности, рассмотренные выше. Корректировка формул заключается в том, что получаемую прибыль уменьшают на величину взимаемых налогов и на размер уплаченных комиссионных. В качестве затрат учитывается не только цена, по которой покупается бумага, но и комиссионные брокерской фирмы. Приведем пример такой корректировки для ГКО. Так формулы (2.12) и (2.19) соответственно примут вид:

	(2.25)
	(2.26)

где: Tax – ставка налога на ГКО (ставка налога подставляется в формулу в десятичном значении, например, налог 15% следует учесть в формуле как 0,15); k – комиссионные платежи как процент от суммы сделки (учитывается в формуле в десятичных значениях).

2. 1. 5. Дюрация

Риск изменения цены облигации, в первую очередь, связан с риском изменения процентных ставок. Поэтому необходимо определить показатель, который являлся бы мерой такого риска. Чтобы определить приблизительное изменение облигации при небольшом изменении доходности до погашения, возьмем первую производную по r для формулы определения цены облигации:

(2.27)

или

(2.28)

или

(2.29)

где: Р – цена облигации, dP – изменение цены облигации, dr – изменение доходности до погашения, r – доходность до погашения, С – купон облигации, N – номинал облигации, п – число лет до погашения облигации.

Сумма в квадратных скобках в правой части уравнения (2.29) представляет собой средневзвешенное время до погашения купонов и номинала облигации, где весами выступают приведенные стоимости платежей.

Например, если облигация погашается через три года, то выражение в квадратных скобках уравнения (2.29) примет вид:

где: 1, 2 и 3 – годы, когда выплачивается купоны и номинал по облигации. Первый год входит в уравнение с удельным весом (приведенная стоимость первого купона), 2-ой – с удельным весом и 3-й – .

С помощью уравнения (2.29) можно приблизительно определить изменение цены облигации при малом изменении доходности до погашения.

Разделим обе части уравнения (2.29) на Р

(2.30)

Уравнение (2.30) говорит о приблизительном процентном изменении цены облигации.

Величину 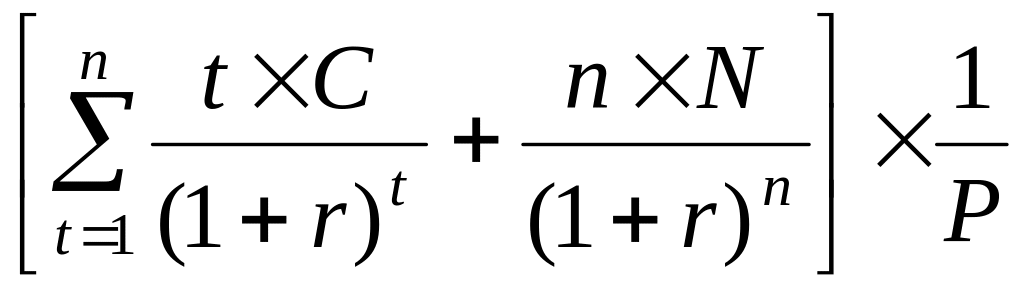в правой части уравнения (2.30) называют дюрацией (duration – протяженностью) Макоули. Обозначим ее через D. Дюрация представляет собой эластичность цены облигации по процентной ставке и поэтому служит мерой риска изменения цены облигации при изменении процентной ставки.

Наглядно можно показать следующим образом. Продифференцируем уравнение (2.2) по (1 + r).

(2.31)

Умножив обе части уравнения (2.31) на , получаем:

или

или

(2.32)

Левая часть уравнения (2.32) – это эластичность цены облигации относительно доходности до погашения (или более точно, относительно (1+r)).

Как видно из уравнения (2.32), чем меньше величина дюрации, тем в меньшей степени цена облигации будет реагировать на изменение процентной ставки и наоборот. Перед дюрацией стоит знак минус. Это говорит о том, что доходность до погашения и цена облигации изменяются в противоположном направлении.

Пример 2.15. Номинал облигации 1 млн. руб., купон 10% и выплачивается один раз в год, до погашения остается 3 года, доходность до погашения 10%. Цена облигации равна 1 млн. руб. Определить дюрацию облигации.

Она равна:

года.

Допустим, что доходность до погашения выросла на 1%, тогда цена облигации снизилась до

руб.

Найдем процентное изменение цены облигации в результате изменения доходности до погашения:

или – 2,44%.

Как видно из примера, дюрация облигации равна 2,74 года, и при небольшом изменении процентной ставки процентное изменение цены облигации составило 2, 44%. Таким образом, дюрация облигации приблизительно говорит о том, на сколько процентов изменится цена облигации при изменении ее доходности на небольшой процент. Показатель дюрации можно использовать не только в отношении облигаций, но и других активов, которые предполагают известные суммы выплат. Дюрация облигации с нулевым купоном равна периоду времени, который остается до ее погашения.

Дюрация определяется в купонных периодах. Если купоны выплачиваются 1 раз в год, то величина дюрации равна количеству лет. Если купоны выплачиваются т раз в год, то дюрацию в годах можно определить по следующей формуле:

(2.33)

где: m – число периодов, за которые выплачиваются купоны в течение года.

Пример 2.16.

Дюрация облигации в купонных периодах равна 7,4 года. Купоны выплачиваются два раза в год. Определить дюрацию в годах.

Она равна:

Запишем формулу (2.30), обозначив дюрацию через D.

(2.34)

Величину называют модифицированной дюрацией. Обозначим ее через D_m. Тогда формула (2.34) примет вид:

(2.35)

Модифицированная дюрация говорит о том, на сколько процентов изменится цена облигации при изменении доходности до погашения на небольшой процент. Эта зависимость станет более наглядной, если уравнение (2.35) представить следующим образом:

(2.36)

Продолжим пример 2.15 и рассчитаем модифицированную дюрацию для облигации, если дюрация Макоули, как мы определили, равна 2, 74 года.

лет

Модифицированная дюрация измеряется в купонных периодах. Если купоны выплачиваются один раз в год, то значение модифицированной дюрации означает количество лет. Если купоны выплачиваются m раз в год, то модифицированную дюрацию в годах можно определить по следующей формуле:

(2.37)

где m – число периодов, за которые выплачиваются купоны.

На рис.2.8 представлено решение примера 2.15 с использованием стандартных финансовых функций Excel.

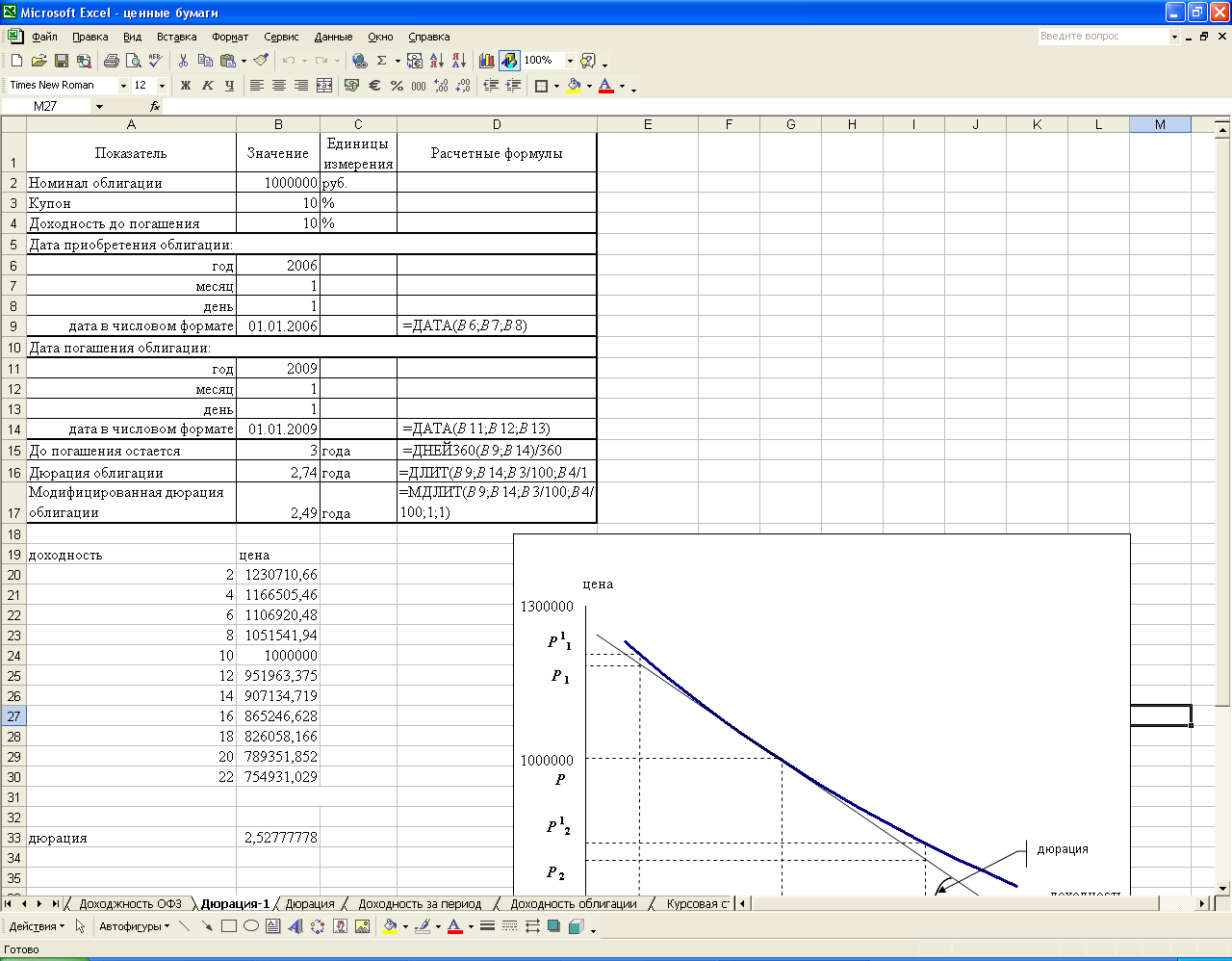
Рис. 2.8. Экранная форма решения примера 2.15

Продолжая пример 2.15, определим, на какую величину в процентах изменится цена облигации при повышении доходности до погашения на 1%. Она равна:

или 2,49%.

Как мы рассчитали выше, действительное падение составило 2,44%. Преобразуем уравнение (2.35) следующим образом:

(2.38)

Выражение в правой части уравнения (2.38) называют дюрацией в денежном выражении. Если мы умножим обе части уравнения (2.38) на dr, то получим уравнение:

(2.39)

Уравнение (2.39) позволяет определить изменение цены облигации при изменении доходности до погашения на небольшую величину.

В примере 2.15 D_m = 2,49 и Р = 1000000 руб. Тогда при росте доходности до погашения облигации на 0,01% ее цена изменится согласно уравнению (2.39) на:

руб.

Действительное изменение цены в этом случае составляет 248,64 руб. Таким образом, при малых изменениях доходности до погашения формула (2.37) дает хорошее приближение величины изменения цены облигации. Графически дюрация представлена на рис. 2.9. Она представляет собой угол наклона касательной к графику цены облигации. Как следует из рис. 2.9, для больших изменений доходности до погашения облигации дюрация дает значительную погрешность. Поскольку дюрация представлена касательной к кривой цены, то при падении доходности до погашения она занижает действительное изменение цены облигации, а при росте доходности до погашения – завышает. Так, при падении доходности с r до r₁ цена облигации вырастет на величину (P₁¹ – Р), дюрация же даст оценку увеличения только на величину (P₁ – Р). При росте доходности до погашения с r до r₂ цена облигации понизится только на величину (P – Р₂). Дюрация даст более значительную оценку изменения цены на величину (Р – Р₂¹).

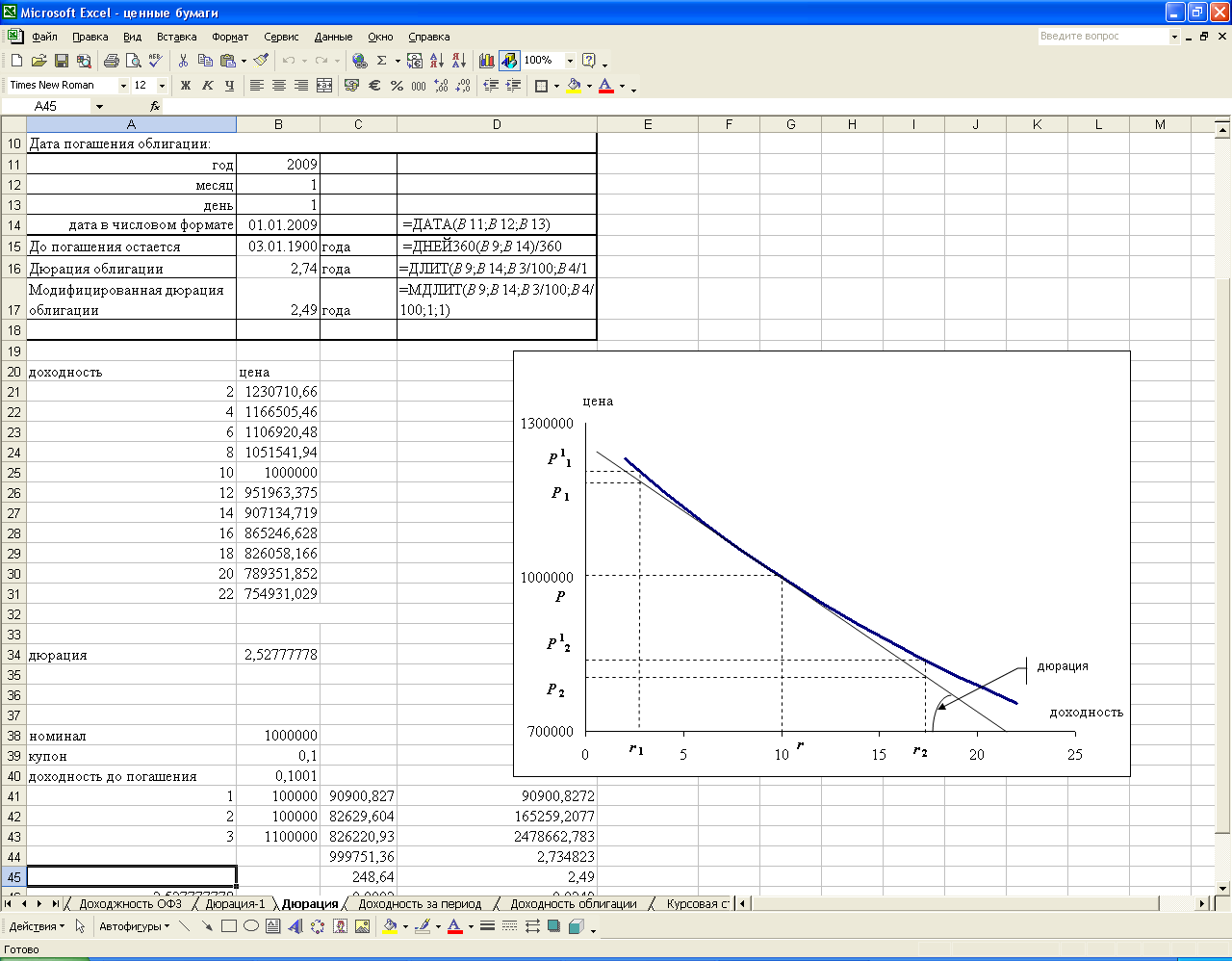
Рис. 2.9. Графическое изображение дюрации

Дюрация, в том числе модифицированная, имеет следующие характеристики:

1) Она меньше времени до погашения облигации или равна ей в случае облигации с нулевым купоном. Модифицированная дюрация бескупонной облигации также меньше времени до ее погашения.

2) Как правило, чем меньше купон облигации, тем больше дюрация, так как больший уддельный вес выплат по облигации приходится на момент ее погашения. Чем выше купон облигации, тем меньше ее дюрация.

3) При прочих равных условиях, чем больше время до погашения облигации, тем больше дюрация.

4) Чем больше дюрация, тем выше риск изменения цены облигации.

5) При повышении доходности до погашения дюрация уменьшается, при понижении доходности до погашения дюрация возрастает.

Иммунизация облигации

Для купонной облигации существует риск реинвестирования купонов. Он заключается в том, что при падении процентных ставок купоны реинвестируются под более низкий процент, при повышении ставок – под более высокий. Изменение процентных ставок также оказывает влияние и на цену облигации, но в противоположном направлении. Таким образом, при повышении ставок инвестор будет проигрывать в цене облигации, но выигрывать от реинвестирования купонов. Напротив, при падении доходности он выигрывает от роста цены облигации, но проигрывает в реинвестировании купонов. Поскольку изменение цены облигации и доходов от реинвестирования купонов имеют противоположную направленность, можно найти точку во времени (в течение срока обращения облигации), где эти два процесса уравновешивают друг друга и доходность операции для инвестора остается неизменной. Такая точка во времени и представлена дюрацией облигации. Например, инвестор купил облигацию с доходностью до погашения 10%, дюрацией 3 года, до погашения которой остается 5 лет. Через некоторое время доходность до погашения данной облигации выросла. Если он продаст облигацию через 3 года, то реализованная доходность его операции составит 10%. Таким образом, инвестор может обезопасить себя от изменения процентных ставок на рынке, или иммунизировать облигацию для периода времени в 3 года. Если он продаст облигацию раньше или позже трех лет, то реализованная доходность, как правило, будет отличаться от 20%. В этом случае инвестор подвергается риску изменения процентной ставки.

Величина дюрации дает хорошее приближение изменения цены облигации только для малых значений изменения доходности до погашения. Поэтому, если в нашем примере доходность до погашения облигации сильно изменится, то она уже не будет иммунизирована на период 3 года, и инвестор не обеспечит себе реализованную доходность в 10% на этот момент времени. Если процент вырастет, то дюрация уменьшится и соответственно временная точка иммунизации облигации составит меньше трех лет, и наоборот. Принцип иммунизации можно использовать при управлении портфелем облигаций.