2. ОПРЕДЕЛЕНИЕ КУРСОВОЙ СТОИМОСТИ И ДОХОДНОСТИ

ЦЕННЫХ БУМАГ

2. 1. Определение курсовой стоимости и доходности облигаций

2. 1. 1. Определение курсовой стоимости облигации

Определение курсовой стоимости ценных бумаг основано на принципе дисконтирования. Инвестор приобретает ценную бумагу, чтобы получать доходы, которые она приносит. Поэтому для ответа на вопрос, сколько сегодня должна стоить та или иная ценная бумага, необходимо определить дисконтированную стоимость всех доходов, которые она принесет.

Технику определения курсовой стоимости можно представить в три действия:

1. определяем поток доходов, который ожидается по ценной бумаге;

2. находим дисконтированную (сегодняшнюю) стоимость величины каждого платежа по бумаге;

3. суммируем дисконтированные стоимости.

Полученная сумма и представляет собой курсовую стоимость ценной бумаги.

Определение курсовой стоимости купонной облигации

Пример 2.1. Номинал облигации равен 1 млн. руб., купон – 10%, выплачивается один раз в год, до погашения остается три года. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в 15%. Определить курсовую стоимость бумаги.

Решение.

1) Определяем поток доходов, который принесет облигация инвестору за три года. В конце каждого года инвестор получит купон в сумме 200 тыс. руб., и в конце третьего года ему выплатят сумму номинала в размере 1 млн. руб. Таким образом, облигация принесет следующий поток доходов:

Годы:	1	2	З
Сумма, тыс. руб.:	100	100	1100

2) Определяем дисконтированную стоимость суммы каждого платежа по облигации.

Для первого платежа она равна:

Для второго платежа:

Для третьего платежа:

3) Определяем цену облигации:

Запишем формулу определения цены облигации в символах:

(2.1)

где: Р – цена облигации, С – купон; N – номинал; n – число лет до погашения облигации; r – доходность до погашения облигации (доходность к погашению).

В Excel существует большой набор стандартных финансовых функций, которые позволяют упростить расчеты с ценными бумагами. Например, расчет по вышеприведенному примеру можно произвести с использованием функции Цена (см. рис. 2.1.).

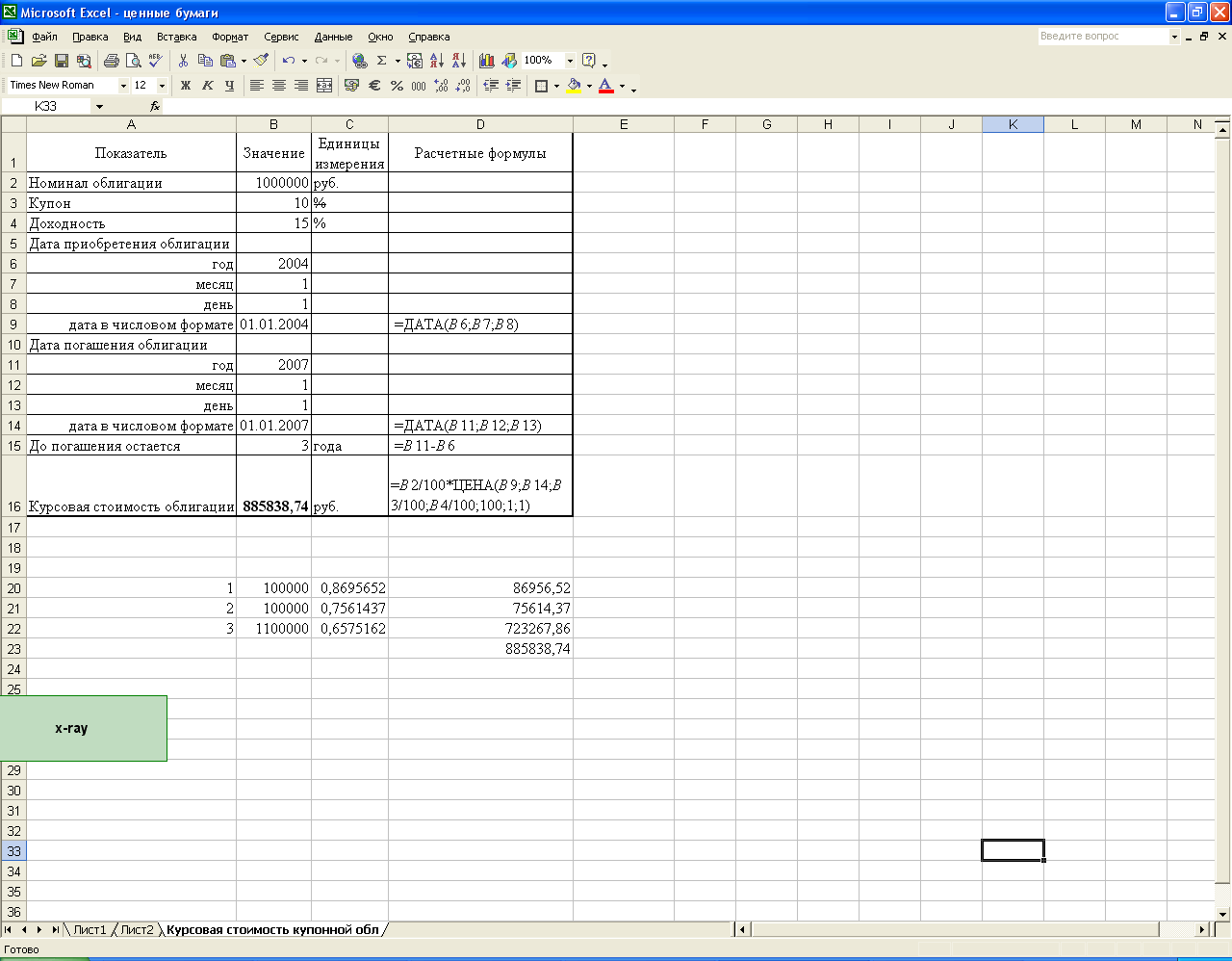
Рис. 2.1. Экранная форма определения курсовой стоимости купонной облигации

В формуле (2.1) важно отметить, что n – это количество лет, которые остаются до погашения бумаги. Например, облигация выпущена на 10 лет, однако 7 лет уже прошло. Определяя курсовую стоимость такой бумаги, следует взять n равной трем. Это вытекает из принципа дисконтирования будущих доходов. В данном случае облигация принесет доходы инвестору только за три оставшиеся года.

В формуле (2.1) появилось такое понятие как доходность до погашения (или доходность к погашению). Доходность до погашения – это доходность в расчете на год, которую обеспечит себе инвестор, если, купив облигацию, продержит ее до погашения. В нашем примере, заплатив за облигацию 885838,74 руб., вкладчик обеспечил себе ежегодную доходность из расчета 15% годовых. Если владелец облигации продаст ее до момента погашения, то, как правило, он не получит данного уровня доходности, так как конечный результат его операции будет зависеть от цены продажи облигации на рынке.

Формулу (2.1) можно записать в более компактной форме:

(2.2)

Наиболее важным моментом при расчете цены облигации является определение ставки дисконтирования. Она должна соответствовать уровню риска инвестиций. В нашем примере данная ставка составляла 15%. На практике ее можно взять, например, из котировок, брокерских компаний по облигациям с похожими характеристиками. Ее также можно попытаться определить аналитически, разложив ставку на составные части. Ставку дисконтирования можно представить следующим образом:

где: – ставка без риска, т. е. ставка по инвестициям, для которых отсутствует риск; в качестве такой ставки берут доходность по государственным ценным бумагам для соответствующих сроков погашения, – премия за ликвидность, – темп инфляции, – реальная ставка процента.

Ставка без риска ( ) может учитывать инфляцию. Однако если инвестор полагает, что инфляция будет развиваться более высоким темпом, он также учтет это в ставке дисконтирования. Приобретая бумагу, инвестор сталкивается с риском ликвидности, который связан с тем, насколько быстро и по какой цене можно продать бумагу. Поэтому данная величина должна найти отражение в ставке дисконтирования.

Ставку дисконтирования также можно определить аналитически.

Пример 2.2. N = 1млн. руб., купон – 10%, доходность до погашения – 8%, до погашения остается три года.

Цена облигации равна:

В данном случае цена облигации оказалась выше номинала. Такая ситуация объясняется тем, что, согласно условиям примера, рынок требует по облигации доходность до погашения на уровне 8% годовых. Однако по ней выплачивается более высокий купон – 10%. Каким образом инвестор может получить более низкую доходность, чем 10%? Это возможно лишь в том случае, если он приобретет облигацию по цене выше номинала. При погашении облигации ему выплатят только номинал. Поэтому сумма премии, которую он уплатил сверх номинала, уменьшит доходность его операции до 8%.

Между курсовой стоимостью и доходностью до погашения облигации существуют следующие зависимости.

1) Цена облигации и доходность до погашения находятся в обратной связи. При повышении доходности цена облигации падает, при понижении – возрастает.

2) Если доходность до погашения выше купонного процента, облигация продается со скидкой.

3) Если доходность до погашения ниже купонного процента, облигация продается с премией.

4) Если доходность до погашения равна купонному проценту, цена облигации равна номиналу.

5) При понижении доходности до погашения на 1% цена облигации возрастает в большей степени в сравнении с ее падением при увеличении доходности до погашения на 1%.

Как уже отмечалось, котировки облигаций приводятся в процентах к номинальной стоимости. Поэтому при определении курсовой стоимости облигации можно пользоваться не величинами в денежном выражении, а в процентах. В этом случае номинал принимается за 100%. В качестве иллюстрации запишем приведенный выше пример с использованием процентов:

Купон по облигации может выплачиваться чаще, чем один раз в год. В таком случае формула (63) примет вид:

(2.3)

где m – частота выплаты купона в течение года.

Как видно из формулы (2.3), количество слагаемых увеличивается в m раз. Дополним пример 2.2 условием, что купон выплачивается два раза в год, и найдем цену облигации:

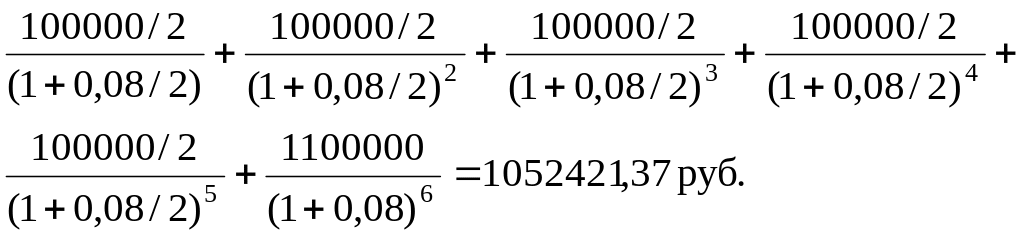
На рис 2.2. приведены расчеты курсовой стоимости купонных облигаций при различной частоте выплат купона в течение года в среде Excel.

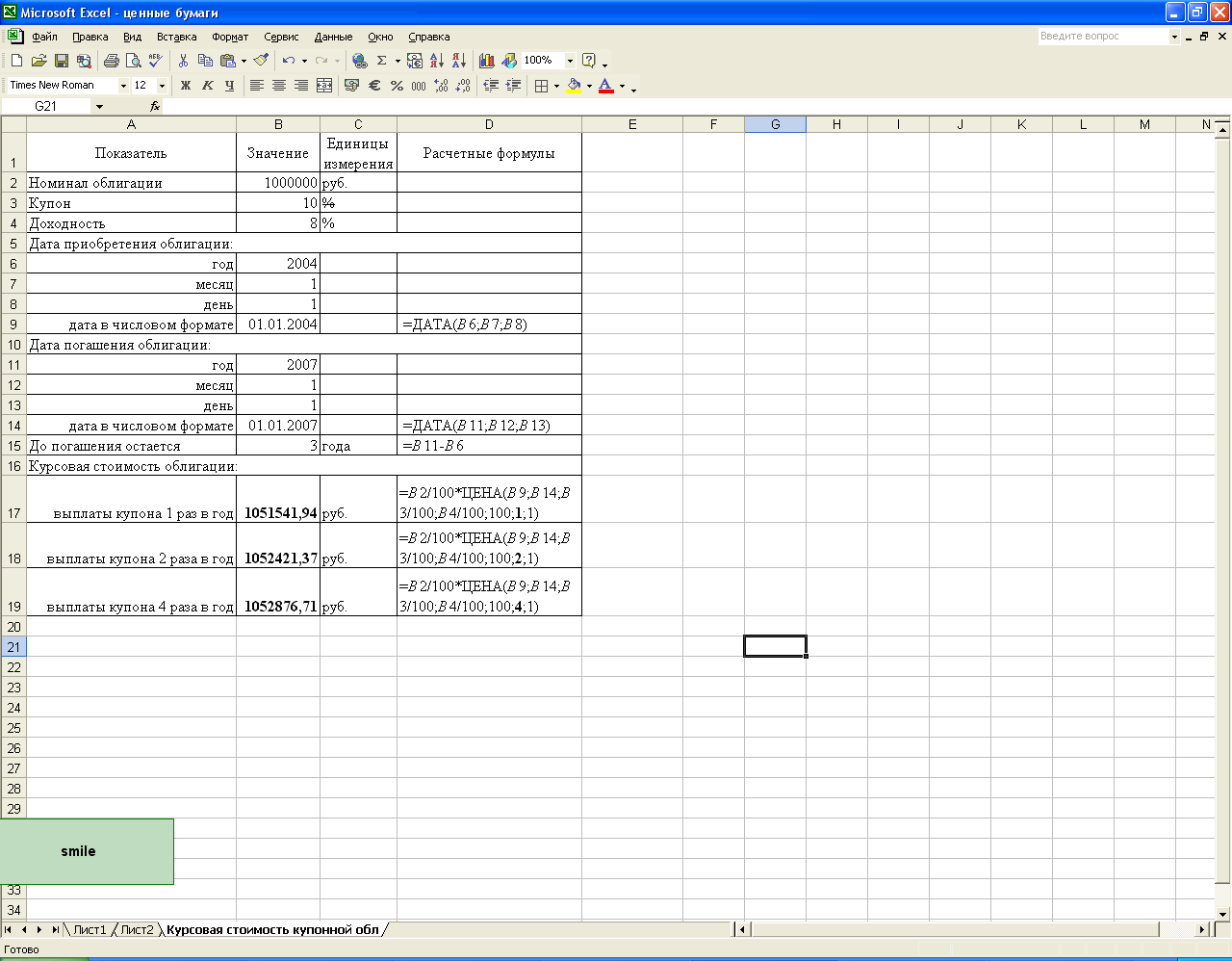
Рис. 2.2. Определения курсовой стоимости купонной облигации при различной частоте выплат купона

Формулы (2.2) и (2.3) можно привести к более удобному виду, учитывая тот факт, что выплата купонов представляет собой не что иное как аннуитет:

(2.4)

и

(2.5)

или

(2.6)

и

(2.7)

Приведенные формулы позволяют рассчитать чистую цену облигации, т.е. цену на основе целых купонных периодов. Однако бумаги продаются и покупаются также в ходе купонного периода. Поэтому следует ответить на вопрос, каким образом рассчитать полную цену облигации, т. е. цену, скорректированную на размер накопленных к моменту сделки суммы купонных процентов. Общий подход и в данном случае остается прежним, т. е. необходимо дисконтировать будущие доходы с учетом времени, которое остается до их получения.

Пример 2.3.

N = 100 тыс. руб., r = 20%, купон равен 10% и выплачивается один раз в год. До погашения облигации остается 2 года 345 дней. Определить цену облигации.

Она равна:

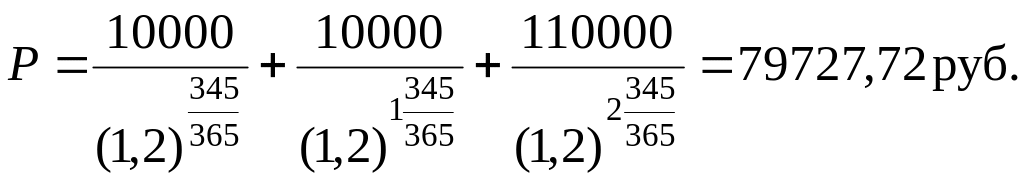
В данном примере первый купон инвестор получит через 345 дней, второй – через год 345 дней и третий купон вместе с номинальной стоимостью – через два года 345 дней. В общем виде формула определения цены облигации для случая, когда купон выплачивается один раз в год, имеет следующий вид:

(2.8)

где , t – число дней с момента сделки до выплаты очередного купона; п – целое число лет, которое остается до погашения облигации, включая текущий год.

Если купон выплачивается m раз в год, то число купонных периодов в формуле (2.8) корректируется на m, как было показано выше, а в знаменателе формулы (2.8) вместо 365 дней указывается число дней в купонном периоде.

Определение курсовой стоимости среднесрочной и долгосрочной бескупонных облигаций

Формулу определения курсовой стоимости бескупонной облигации можно получить из формулы (2.8). Поскольку по облигации не выплачиваются купоны, то С = 0 и формула (2.8) принимает вид:

(2.9)

Пример 2.4.

N = 10000 руб., r = 10%, п = 3 года. Определить Р.

Если до погашения облигации остается не целое число лет, то формула (2.9) примет вид:

(2.10)

где , t – число дней от момента сделки до начала целого годового периода для облигации; п – целое число лет, которое остается до погашения облигации, включая текущий год.

На практике приходится сравнивать купонные и бескупонные облигации. В этом случае необходимо помнить о следующем правиле. Если по купонным облигациям процент выплачивается m раз в год, то для того, чтобы иметь единую частоту начисления сложного процента во всех финансовых расчетах формулу (2.9) следует также скорректировать на m, а именно:

(2.11)

Определение курсовой стоимости ГКО

Цена ГКО определяется по формуле:

(2.12)

где N – номинал ГКО; r – доходность до погашения; t – количество дней от момента сделки до погашения ГКО.

Пример 2.5.

N = 1 млн. руб., t = 60 дней, r = 10%. Определить цену ГКО.

Она равна:

Определение курсовой стоимости ОФЗ-ПК и ОГСЗ

Цена данных облигаций определяется стандартным способом, т. е. будущие доходы по облигациям дисконтируются к сегодняшнему дню и суммируются. Особенностью ОФЗ-ПК и ОГСЗ является то, что купоны у них плавающие и их величина изменяется в зависимости от ситуации на рынке ГКО. Поэтому инвестору необходимо вначале сделать прогноз относительно ситуации на рынке ГКО. Затем оценить величину будущих купонов и дисконтировать их и номинал к сегодняшнему дню.

Были рассмотрены формулы определения курсовой стоимости облигаций. Они позволяют инвестору рассчитать приемлемый для него уровень цены бумаги. В то же время это не означает, что облигации на рынке обязательно будут продаваться по найденной цене. Так происходит потому, что различные вкладчики по разному могут оценивать риск приобретения облигации, и, следовательно, использовать несколько отличные ставки дисконтирования. Кроме того, на цену будут также влиять силы спроса и предложения. Если спрос превышает предложение, то это создаст потенциал к повышению цены, если предложение больше спроса, то – то к понижению.

2. 1. 2. Определение доходности облигаций

Определение доходности купонной облигации

Текущая доходность определяется по формуле:

(2.13)

где: – текущая доходность; С – купон облигации; Р – текущая цена облигации.

Пример 2.6.

С = 20000 руб., Р = 80000 руб. Определить текущую доходность облигации.

Она равна:

или 25%.

Текущая доходность представляет собой как бы фотографию доходности облигации на данный момент времени. В знаменателе формулы (2.13) стоит текущая цена облигации. В следующий момент она может измениться, тогда изменится и значение текущей доходности.

Показателем текущей доходности удобно пользоваться, когда до погашения облигации остается немного времени, так как в этом случае ее цена вряд ли будет испытывать существенные колебания.

Более объективным показателем доходности является доходность до погашения, так как при ее определении учитывается не только купон и цена бумаги, но и период времени, который остается до погашения, а также скидка или премия относительно номинала. Доходность облигации можно вычислить из формулы (2.2). Поскольку она содержит степени, то сразу определить доходность можно только с помощью специальной компьютерной программы. Можно воспользоваться также методом подстановки. Он состоит в том, что в формулу (2.2) последовательно подставляют различные значения доходности до погашения и определяют соответствующие им цены. Операцию повторяют до тех пор, пока значение рассчитанной цены не совпадет с заданной ценой. При совпадении цен мы получим искомую величину доходности до погашения. Поскольку цена и доходность облигации связаны обратной зависимостью, то в ходе подстановки, получив цену, которая выше данной, необходимо увеличить следующую цифру доходности, подставляемую в формулу. Если рассчитанная цена оказалась ниже заданной, необходимо уменьшить значение доходности.

В ряде случаев для принятия решения достаточно определить только ориентировочный уровень доходности бумаги. Формула определения ориентировочной доходности облигации имеет следующий вид:

(2.14)

где r – доходность до погашения; N – номинал облигации; Р – цена облигации;

п – число лет до погашения; С – купон.

Пример 2.7.

N =1000 руб., Р = 850 руб., n = 4 года, купон равен 15%. Определить доходность до погашения облигации.

Она равна:

или 20,27%.

Погрешность формулы (2.14) тем больше, чем больше цена облигации отличается от номинала и чем больше лет остается до погашения облигации. Если бумага продается со скидкой, то формула (2.14) дает заниженное значение доходности облигации, если с премией, то завышенное.

После того как инвестор определил значение доходности облигации с помощью формулы (2.14), он может воспользоваться формулой (2.15) для вычисления точной цифры доходности:

(2.15)

Техника вычисления доходности по формуле (2.15) сводится к следующему. Вкладчик выбирает значение , которое ниже полученного значения ориентировочной доходности, и рассчитывает для него соответствующую цену облигации P₁, воспользовавшись формулой (2.2). Далее берет значение r₂, которое выше значения ориентировочной доходности, и рассчитывает для него цену Р₂. Полученные значения подставляются в формулу (2.15).

Продолжение примера 2.7.

Определить точную величину доходности облигации из приведенной выше задачи.

Мы рассчитали, что ориентировочная доходность облигации равна 20,27%. Поэтому возьмем r₁, = 20% и r₂ = 21%. Тогда P₁ = 870, 56 руб. и Р₂ = 847, 57 руб.

Отсюда

Таким образом, купив облигацию за 850 руб., инвестор обеспечит себе доходность до погашения равную 20, 89%.

Для расчета точного значения доходности облигации в среде Excel можно использовать стандартную финансовую функцию Доход (см. рис. 2.3.)

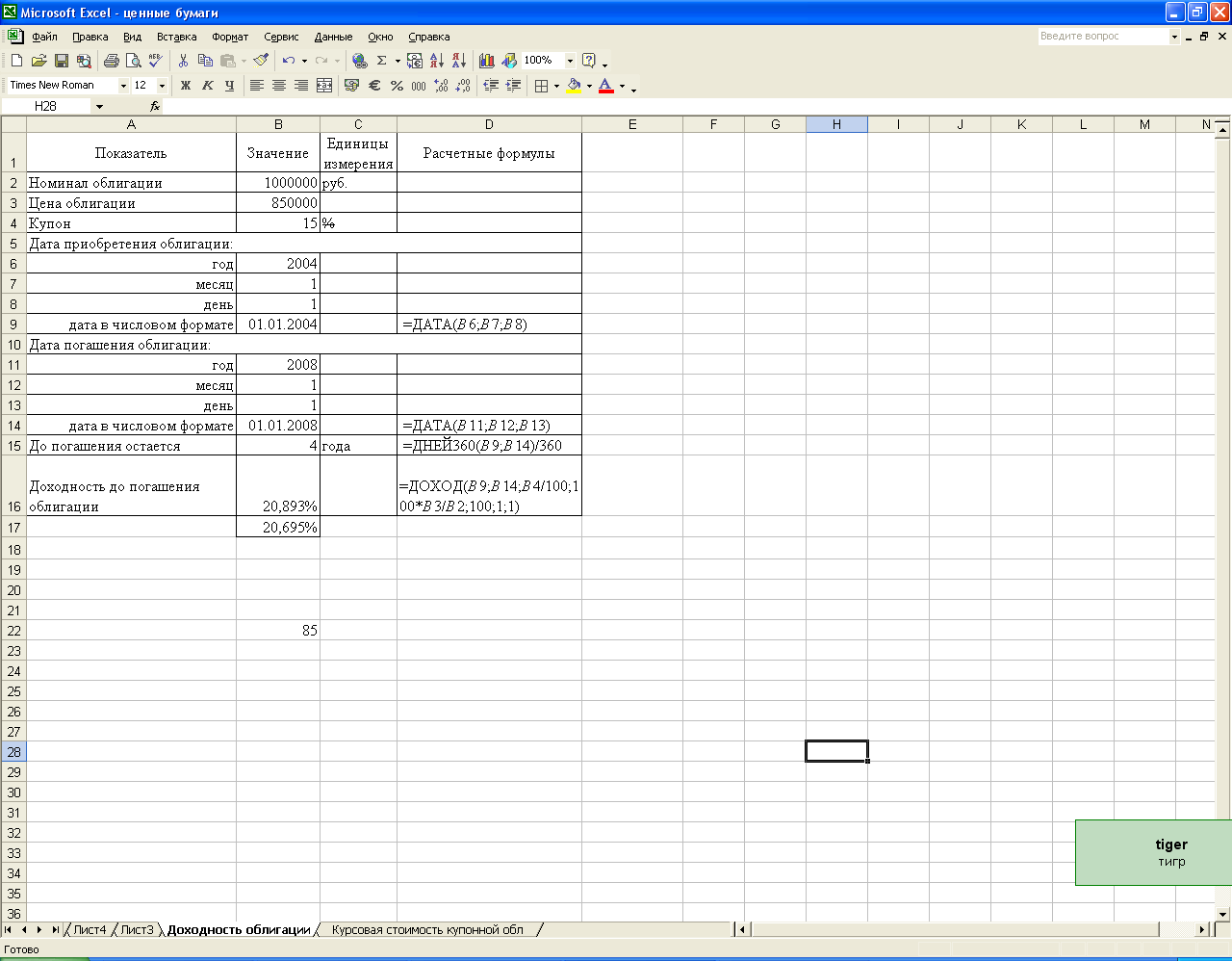
Рис. 2.3. Экранная форма решения примера 2.7

В формуле (2.14) купон выплачивался один раз в год. Соответственно в ответах получалось значение r равное простому проценту в расчете на год. Если по облигации купон выплачивается m раз в год, то можно пользоваться указанной формулой без всяких корректировок, т. е. не умножать количество лет на m и не делить купон на m. В этом случае мы также получим доходность бумаги как простой процент в расчете на год. В то же время, можно определить значение доходности, сделав указанную корректировку. Например, для облигации, по которой купон выплачивается два раза в год, формула ориентировочной доходности примет следующий вид:

(2.16)

Однако в этом случае r является доходностью за полгода. Чтобы получить доходность за год, необходимо полученное значение умножить на 2.

Определение доходности бескупонной облигации

Доходность до погашения облигации с нулевым купоном определяется из формулы (2.17), которая вытекает из формулы (2.9).

(2.17)

Пример 2.8.N = 1000 руб., Р = 850 руб., п = 4 года. Определить доходность облигации.

Она равна:

или 4,147%.

Если подавляющая часть купонных облигаций имеет купоны, которые выплачиваются m раз в год, то формулу (2.17) необходимо скорректировать на величину m, т. е.:

(2.18)

Пример 2.9.N = 1000 руб., Р = 850 руб., n = 4 года, m = 2. Определить доходность облигации.

Она равна:

или 4,105%.

На рис. 2.4 представлено определение доходности бескупонной облигации на основе исходных данных примеров 2.8 и 2.9 в среде Excel.

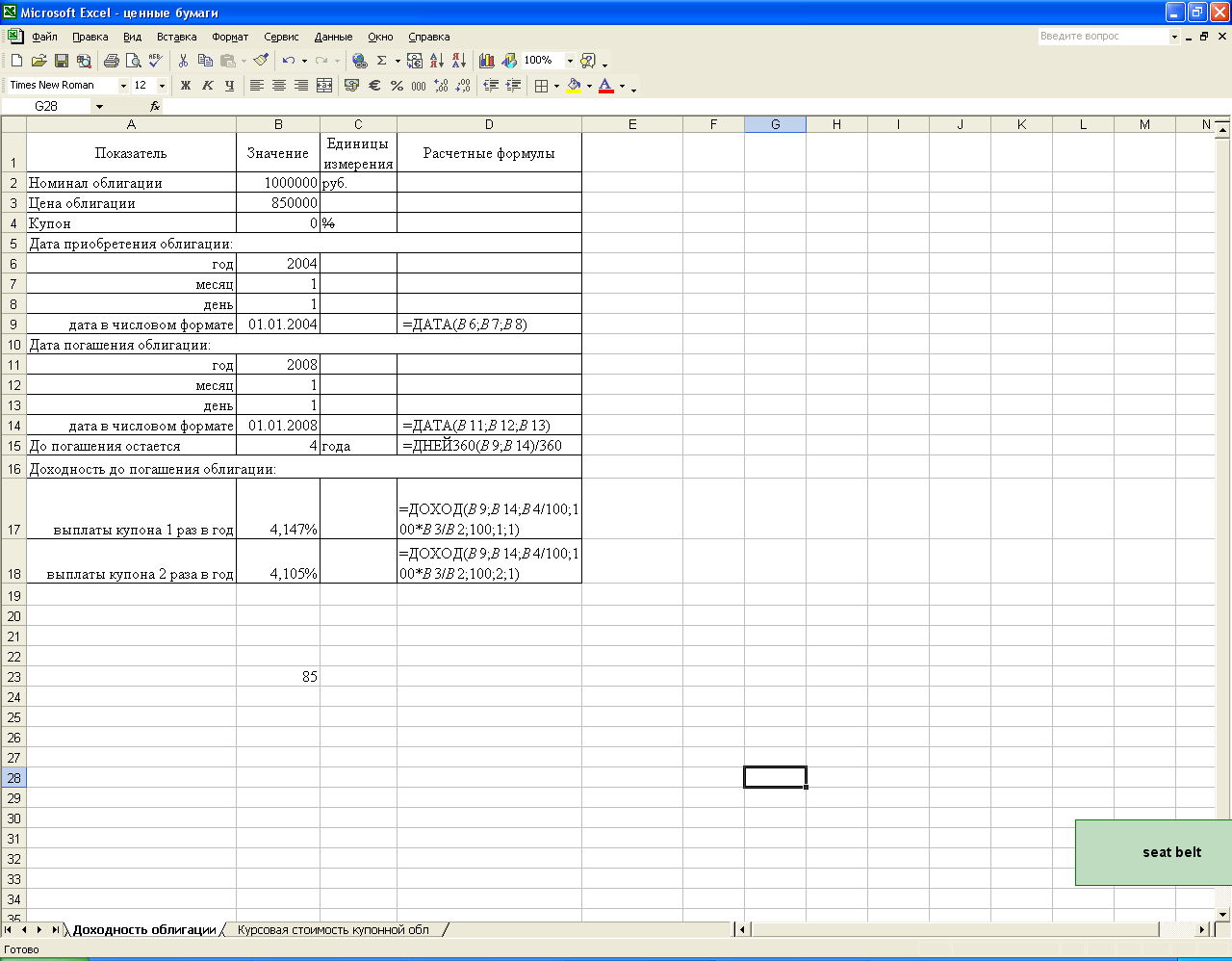
Рис. 2.4. Экранная форма решения примеров 2.8 и 2.9