
Построение уравнений множественной линейной регрессии
Пример 1
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника Y (тыс. р.) от ввода в действие новых основных фондов X1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих X2 (%).
Номер |
Y |
X1 |
X2 |
Номер |
Y |
X1 |
X2 |
1 |
7 |
3,9 |
10 |
11 |
9 |
6 |
21 |
2 |
7 |
3,9 |
14 |
12 |
11 |
6,4 |
22 |
3 |
7 |
3,7 |
15 |
13 |
9 |
6,8 |
22 |
4 |
7 |
4 |
16 |
14 |
11 |
7,2 |
25 |
5 |
7 |
3,8 |
17 |
15 |
12 |
8 |
28 |
6 |
7 |
4,8 |
19 |
16 |
12 |
8,2 |
29 |
7 |
8 |
5,4 |
19 |
17 |
12 |
8,1 |
30 |
8 |
8 |
4,4 |
20 |
18 |
12 |
8,5 |
31 |
9 |
8 |
5,3 |
20 |
19 |
14 |
9,6 |
32 |
10 |
10 |
6,8 |
20 |
20 |
14 |
9 |
36 |
Необходимо:
Оценить показатели вариации каждого признака и сделать вывод о возможностях применения метода наименьших квадратов для их изучения.
Определить линейные коэффициенты парной корреляции и выявить неинформативные факторы.
Определить уравнение множественной линейной регрессии и оценить значимость его параметров с помощью t-критерия Стьюдента.
Оценить статистическую надежность уравнения регрессии и коэффициента множественной детерминации с помощью F-критерия Фишера.
Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.
Оценить полученные результаты.
Решение
1. Введите исходные данные. В главном меню выберите последовательно пункты Сервис/Анализ данных/Описательная статистика, щелкните по кнопке ОК. В диалоговом окне задаются:
Входной интервал – диапазон, содержащий анализируемые данные;
Группирование – по столбцам или по строкам;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Выходной интервал – левая верхняя ячейка будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа.
Результаты размещаются в трех таблицах (Y, X1, X2).
Y |
|
X1 |
|
X2 |
|
Среднее |
9,6 |
Среднее |
6,19 |
Среднее |
22,3 |
Стандартная ошибка |
0,549641 |
Стандартная ошибка |
0,433523 |
Стандартная ошибка |
1,523673 |
Медиана |
9 |
Медиана |
6,2 |
Медиана |
20,5 |
Мода |
7 |
Мода |
3,9 |
Мода |
20 |
Стандартное отклонение |
2,458069 |
Стандартное отклонение |
1,938773 |
Стандартное отклонение |
6,814072 |
Дисперсия выборки |
6,042105 |
Дисперсия выборки |
3,758842 |
Дисперсия выборки |
46,43158 |
Эксцесс |
-1,19605 |
Эксцесс |
-1,33143 |
Эксцесс |
-0,53653 |
Асимметричность |
0,445096 |
Асимметричность |
0,188101 |
Асимметричность |
0,327801 |
Интервал |
7 |
Интервал |
5,9 |
Интервал |
26 |
Минимум |
7 |
Минимум |
3,7 |
Минимум |
10 |
Максимум |
14 |
Максимум |
9,6 |
Максимум |
36 |
Сумма |
192 |
Сумма |
123,8 |
Сумма |
446 |
Счет |
20 |
Счет |
20 |
Счет |
20 |
Коэффициенты вариации для трех выборок vy, vx1, vx2 рассчитываются по формуле:
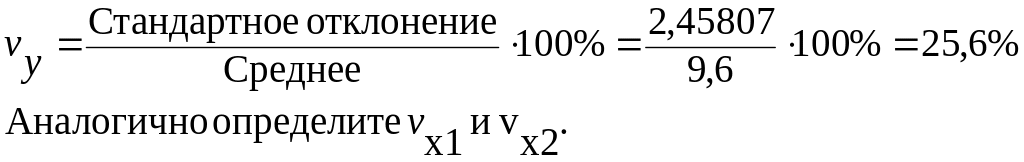
Если коэффициенты вариации не превышают 35%, то совокупность предприятий однородна и можно использовать метод наименьших квадратов для ее анализа.
2. В главном меню последовательно выберите пункты Сервис/Анализ данных/Корреляция. Щелкните по кнопке OK. В диалоговом окне задаются:
Входной интервал – диапазон, содержащий анализируемые данные;
Группирование – по столбцам или по строкам;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Выходной интервал – левая верхняя ячейка будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа.
Результаты размещаются в таблице коэффициентов парной корреляции.
|
Y |
X1 |
X2 |
Y |
1 |
|
|
X1 |
0,969881 |
1 |
|
X2 |
0,9408 |
0,942839 |
1 |
Считается, что две переменные коллинеарны, т. е. находятся между собой в линейной зависимости, если коэффициент парной корреляции между ними не меньше 0,7. При наличии коллинеарности факторов исключают фактор, у которого коэффициент парной корреляции меньше, чем коэффициент парной корреляции межфакторной связи. Коэффициент парной корреляции межфакторной связи Rx1x2=0,942839, следовательно, межфакторная связь - тесная и превышает тесноту связи x2 и y (Ryx2=0,9408), но меньше чем у x1 и y (Ryx1=0,969881). Сделайте вывод о малоинформативном, недостаточно статистически надежном факторе.
3. Выполните регрессионный анализ. В главном меню выберите пункты Сервис/Анализ данных/Регрессия. По таблице параметров модели и их статистических оценок определите коэффициенты регрессии и оцените значимость коэффициентов регрессии с помощью t-статистик Стьюдента при уровне значимости α=0,05 и d.f.=n-m-1. Табличное значение t-критерия Стьюдента определите при помощи статистической функции СТЬЮДРАСПОБР (α, d.f.). Сделайте выводы.
Таблица параметров модели и их статистических оценок
|
Коэффициенты |
Стандарт-ная ошибка |
t-статис-тика |
P-Значение |
Нижние 95% |
Верхние 95% |
Y-пересе-чение |
1,8353 |
0,4710 |
3,8960 |
0,00116 |
0,8414 |
2,8291 |
X1 |
0,9459 |
0,2125 |
4,4499 |
0,00035 |
0,4974 |
1,3944 |
X2 |
0,0856 |
0,0604 |
1,4155 |
0,17496 |
-0,0419 |
0,2132 |
4. Определите коэффициент множественной детерминации по таблице регрессионной статистики.
Регрессионная статистика |
|
Множественный R |
0,97310 |
R-квадрат |
0,94692 |
Нормированный R-квадрат |
0,94068 |
Стандартная ошибка |
0,59867 |
Наблюдения |
20 |
Оцените статистическую надежность регрессионного уравнения и коэффициента множественной детерминации с помощью F-критерия Фишера, используя таблицу дисперсионного анализа.
Дисперсионный анализ |
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
108,7070 |
54,3535 |
151,653 |
1,45E-11 |
Остаток |
7 |
6,0929 |
0,3584 |
|
|
Итого |
9 |
114,8 |
|
|
|
Табличное значение F-критерия Фишера определите при помощи статистической функции FРАСПОБР (α, k1, k2).
5. Рассчитайте средние частные коэффициент эластичности Эxi, используя статистическую функцию СРЗНАЧ, по формуле:
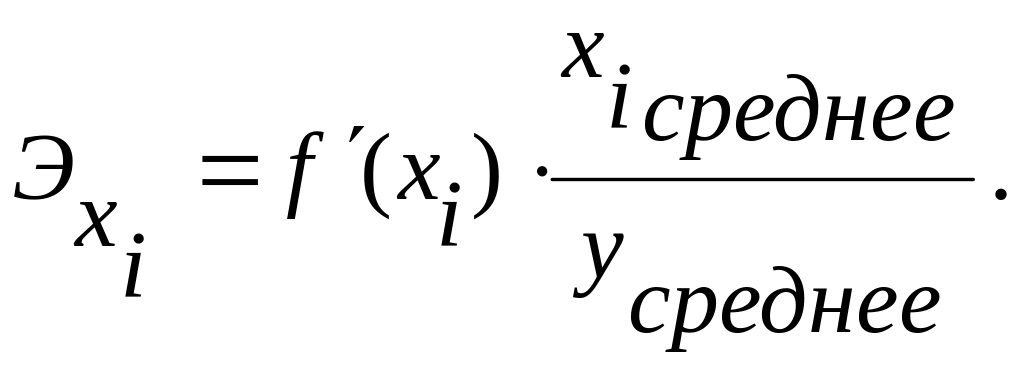
Установите, какой фактор сильнее влияет на результат Y.
Контрольные задания
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
2. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних коэффициентов эластичности.
3. Оцените статистическую значимость параметров регрессионной модели и показателей тесноты связи с помощью t-критерия Стьюдента, F-критерия Фишера при уровне значимости α=0,05.
4. Оцените качество уравнения через среднюю ошибку аппроксимации.
5. Определите матрицу парных коэффициентов корреляции и на их основе отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
6. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений для вариантов №1-12. Рассчитайте прогнозное значение результата для России, если прогнозные значения факторов увеличатся на 3% для вариантов №13-26.
Рассчитайте доверительный интервал прогнозного значения результирующего фактора для 5%-го уровня значимости.
Распечатайте таблицы регрессионного анализа и результаты расчетов.
Имеются данные о деятельности крупнейших компаний США в 1996 году.
Номер компа-нии |
Чистый доход, млрд долл., Y |
Оборот капитала, млрд долл., X1 |
Использован-ный капитал, млрд долл., X2 |
Численность служащих, тыс. чел., X3 |
1 |
6,6 |
6,9 |
83,6 |
222 |
2 |
3 |
18 |
6,5 |
32 |
3 |
6,5 |
107,9 |
50,4 |
82 |
4 |
3,3 |
16,7 |
15,4 |
45,2 |
5 |
0,1 |
79,6 |
29,6 |
299,3 |
6 |
3,6 |
16,2 |
13,3 |
41,6 |
7 |
1,5 |
5,9 |
5,9 |
17,8 |
8 |
5,5 |
53,1 |
27,1 |
151 |
9 |
2,4 |
18,8 |
11,2 |
82,3 |
10 |
3 |
35,3 |
16,4 |
103 |
11 |
4,2 |
71,9 |
32,5 |
225,4 |
12 |
2,7 |
93,6 |
25,4 |
675 |
13 |
1,6 |
10 |
6,4 |
43,8 |
14 |
2,4 |
31,5 |
12,5 |
102,3 |
15 |
3,3 |
36,7 |
14,3 |
105 |
16 |
1,8 |
13,8 |
6,5 |
49,1 |
17 |
2,4 |
64,8 |
22,7 |
50,4 |
18 |
1,6 |
30,4 |
15,8 |
480 |
19 |
1,4 |
12,1 |
9,3 |
71 |
20 |
0,9 |
31,3 |
18,9 |
43 |
Варианты
Номер варианта |
Номера компаний, показатели которых исключены из варианта |
Номер варианта |
Номера компаний, показатели которых исключены из варианта |
1 |
1 |
7 |
1,2,3 |
2 |
1,2 |
8 |
1,3,4 |
3 |
2,3 |
9 |
1,3,5 |
4 |
3,4 |
10 |
1,2,4 |
5 |
4,5 |
11 |
2,3,4 |
6 |
5,6 |
12 |
2,3,5 |
По данным таблицы изучается зависимость индекса человеческого развития от ряда факторов.
Страна |
Индекс человеческого разви-тия, Y |
ВВП 1997 г., % к 1990 г., X1 |
Суточная калорийность питания населения, ккал на душу населения, X2 |
Ожидаемая продолжительность жизни при рождении 1997 г., число лет, X3 |
Австрия |
0,904 |
115 |
3343 |
77 |
Австралия |
0,922 |
123 |
3001 |
78,2 |
Белоруссия |
0,763 |
74 |
3101 |
68 |
Бельгия |
0,923 |
111 |
3543 |
77,2 |
Великобритания |
0,918 |
113 |
3237 |
77,2 |
Германия |
0,906 |
110 |
3330 |
77,2 |
Дания |
0,905 |
119 |
3808 |
75,7 |
Индия |
0,545 |
146 |
2415 |
62,6 |
Испания |
0,894 |
113 |
3295 |
78 |
Италия |
0,9 |
108 |
3504 |
78,2 |
Канада |
0,932 |
113 |
3056 |
79 |
Казахстан |
0,74 |
71 |
3007 |
67,6 |
Китай |
0,701 |
210 |
2844 |
69,8 |
Латвия |
0,744 |
94 |
2861 |
68,4 |
Нидерланды |
0,921 |
118 |
3259 |
77,9 |
Норвегия |
0,927 |
130 |
3350 |
78,1 |
Польша |
0,802 |
127 |
3344 |
72,5 |
Россия |
0,747 |
61 |
2704 |
66,6 |
США |
0,927 |
117 |
3642 |
76,7 |
Украина |
0,721 |
46 |
2753 |
68,8 |
Финляндия |
0,913 |
107 |
2916 |
76,8 |
Франция |
0,918 |
110 |
3551 |
78,1 |
Чехия |
0,833 |
99,2 |
3177 |
73,9 |
Швейцария |
0,914 |
101 |
3280 |
78,6 |
Швеция |
0,923 |
105 |
3160 |
78,5 |
Варианты
Номер варианта |
Страны, показатели которых исключены из варианта |
Номер варианта |
Страны, показатели которых исключены из варианта |
13 |
Индия |
20 |
Чехия |
14 |
Казахстан |
21 |
Австрия |
15 |
Китай |
22 |
Австралия |
16 |
Латвия |
23 |
Бельгия |
17 |
Польша |
24 |
Великобритания |
18 |
Индия, Украина, Китай |
25 |
Канада |
19 |
Украина |
26 |
Норвегия |
