
- •9. Кластерный анализ. Иерархические агломеративные методы.
- •Расстояния между кластерами
- •Иерархические агломеративные методы
- •10. Дискриминантный анализ. Математическая модель.
- •Математическая модель
- •1. Симплекс- метод решения задачи линейного программирования. Симплекс- таблицы.
- •4.Задача вариационного исчисления и правило ее решения.
Многомерные статистические методы
9. Кластерный анализ. Иерархические агломеративные методы.
Кластерный анализ решает задачу классификации объектов при практически отсутствующей априорной информации о наблюдениях внутри классов.
Кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы
Методы кластерного анализа позволяют разбить изучаемую совокупность объектов на группы однородных в некотором смысле объектов, называемых кластерами или классами. Наибольшее распространение получили два подхода к задаче классификации: эвристический, реализующий некоторую схему разделения объектов на классы, исходя из интуитивных соображений, и экстремальный, реализующий схему разделения на основе заданного критерия оптимальности. Наиболее трудным в задаче классификации является определение меры однородности объектов.
Расстояния между кластерами
Пусть
имеется матрица расстоянии
 между
между
 объектами и некоторое их разбиение
объектами и некоторое их разбиение
 на
на
 кластеров. Основным понятием
кластер-процедур является расстояние
кластеров. Основным понятием
кластер-процедур является расстояние
 между кластерами
между кластерами
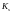 и
и
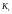 .
Существуют следующие виды расстояний:
.
Существуют следующие виды расстояний:
расстояние, измеряемое по принципу «ближнего соседа»,
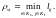 (21)
(21)
Метод, использующий это расстояние, получил в отечественной литературе название метода «ближнего соседа».
Расстояние, измеряемое по принципу «дальнего соседа».
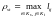 ; (22)
; (22)
Расстояние
по принципу «средней связи»
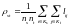 ; (23)
; (23)
где
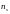 и
и
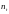 — числа объектов в кластерах
и
;
— числа объектов в кластерах
и
;
Расстояние, измеряемое между «центрами тяжести» кластеров («центроидный метод»),
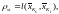 (24)
(24)
где
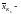 среднее
арифметическое векторных наблюдений
среднее
арифметическое векторных наблюдений
 при
при
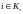 .
.
Названные методы относятся к группе иерархических (деревообразующих) алгомеративных (объединительных) методов.
Иерархические агломеративные методы
Это
многошаговые методы, работающие в такой
последовательности: на нулевом шаге за
разбиение принимается исходная
совокупность
элементарных кластеров, матрица
расстояний между которыми
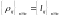 ;
на каждом следующем шаге происходит
объединение (в соответствии с эвристическим
или экстремальным подходом) двух
кластеров
и
,
сформированных на предыдущем шаге, в
один кластер
;
на каждом следующем шаге происходит
объединение (в соответствии с эвристическим
или экстремальным подходом) двух
кластеров
и
,
сформированных на предыдущем шаге, в
один кластер
 (будем его обозначать
(будем его обозначать
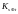 ),
при этом размерность матрицы расстояний
уменьшается, по сравнению с размерностью
матрицы предыдущего шага, на единицу.
При использовании вышеназванных
агломеративных методов рассчитать
расстояние
),
при этом размерность матрицы расстояний
уменьшается, по сравнению с размерностью
матрицы предыдущего шага, на единицу.
При использовании вышеназванных
агломеративных методов рассчитать
расстояние
 между кластерами
и
между кластерами
и
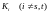 можно, используя соответствующую методу
формулу расстояния между кластерами,
однако менее трудоемки расчеты по
формуле:
можно, используя соответствующую методу
формулу расстояния между кластерами,
однако менее трудоемки расчеты по
формуле:
 (25)
(25)
в которой
значения коэффициентов
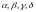 зависят от используемого метода:
зависят от используемого метода:
Метод |
|
|
|
|
|
Ближний сосед (Одиночной связи) |
0.5 |
0.5 |
0 |
-0.5 |
|
Дальний сосед (Полных связей) |
0.5 |
0.5 |
0 |
0.5 |
|
Средней связи |
|
|
0 |
0 |
|
Центроидный |
|
|
|
0 |
|
В последнем столбце: слева приведена формула подсчета , вытекающая из (25), а справа — вытекающая из принятого в соответствующем методе определения расстояний между кластерами.



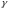

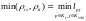 (26)
(26)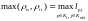 (27)
(27)
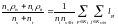 (28)
(28)
 (29)
(29)