7.4. Какие движения оси волчка называются прецессией и нутацией?

В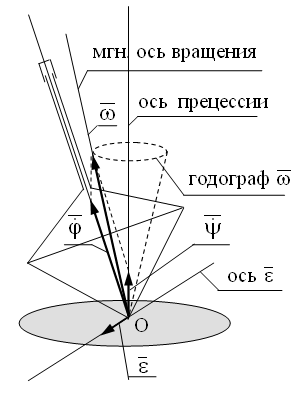 ращение волчка относительно его оси симметрии - есть его собственное вращение.

Вращение оси волчка вокруг вертикали является прецессией.

Медленное изменение угла между осью прецессии и осью собственного вращения во вращающейся плоскости Zoz - нутация.

7.5. Как, зная угловые скорости прецессии, нутации и собственного вращения тела, определить положение его мгновенной оси вращения?

7.6. Каким векторным произведением определяется вектор скорости точки тела при его сферическом движении ?

Скорость движения конца вектора по этой окружности равна векторному произведению вектора угловой скорости прецессии на вектор мгновенной угловой скорости.

Это записывается в виде

Для определения скоростей и ускорений точек тела при его сферическом движении используются векторные формулы, которые были получены для вращающихся тел при введении вектора угловой скорости и вращающейся системы координатных осей.

7.7. Какой вид имеют формулы Эйлера для определения проекций вектора скорости точки на оси координат при сферическом движении тела?

7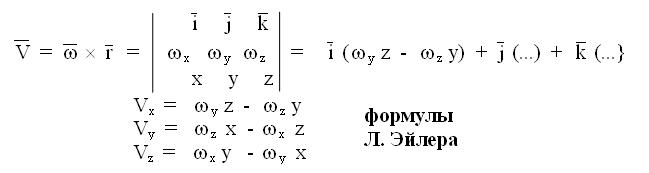 .8. Какая векторная формула определяет ускорение точки тела при его сферическом движении?

В отличие от вращательного при сферическом движении тел осестремительные и вращательные ускорения точек перпендикулярны между собой только в плоскости, проходящей через векторы

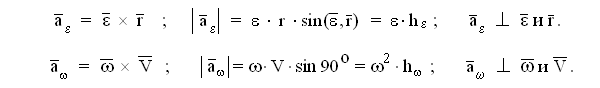
в этих формулах - расстояния от точки до оси углового ускорения и до мгновенной оси вращения тела.

7.9. Как определяется модуль полного ускорения точки тела при его сферическом движении?

Модуль вектора ускорения любой точки определяется как модуль суммы любых двух векторов - т.е. по теореме косинусов.

7.10. Каким векторным произведением определяется вектор углового ускорения тела при его регулярной прецессии?

Цикл 8 к теме “ Плоское движение твердого тела”

8.1. Какое движение тела называют плоским или плоскопараллельным?

Плоскопараллельным или плоским называют движение твердого тела, при котором все точки тела движутся в плоскостях, параллельныхнекоторой неподвижной плоскости.

8.2. Какими уравнениями описывается плоское движение тела?

Для описания плоского движения тел достаточно описать движение точек одного сечения тела плоскостью, параллельной неподвижной плоскости. Уравнения вида :

X_A = X_A (t); Y_A = Y_A (t); φ = φ(t)

называют уравнениями плоского или плоскопараллельного движения твердого тела.

8.3. Что понимается под полюсом при изучении плоского движения тела?

Точку тела, характеристики движения которой известны, в теории плоского движения принято называть полюсом.

8.4. Какие характеристики определяются по уравнениям плоского движения тела?

По уравнениям плоского движения в любой момент времени можно определить положение, скорость и ускорение полюса и характеристики вращательного движения тела - то есть его угловую скорость и его угловое ускорение. Определяются и уравнения движения любой другой точки тела, положение которой относительно полюса задано. Здесь возможны следующие два варианта.

8 .5. Как формулируется теорема о скоростях точек тела при его плоском движении?

Скорость любой точки тела при плоском движении равна геометрической сумме скорости полюса и скорости во вращении точки относительно полюса.

8.6. Что известно о проекциях скоростей точек тела на соединяющую их прямую?

Проекции скоростей точек тела при его плоском движении на прямую, соединяющую точки, равны.

8.7. Какая точка называется мгновенным центром скоростей (М.Ц.С.) движущейся плоской фигуры?

В любой момент непоступательного движения плоской фигуры на плоскости, связанной с фигурой, существует точка, скорость которой равна нулю. Точку эту называют мгновенным центром скоростей ( принятое сокращение - М.Ц.С. ) и обозначают, как правило, буквой Р.

8. Как определить положение М.Ц.С., зная скорость одной из точек тела, его угловую скорость и направление вращения?

8 .9. Как определяется положение М.Ц.С. тела при его плоском движении, если известны направления скоростей двух точек тела?

1. Случай, когда известны направления движения двух точек тела,и эти направления не параллельны.

М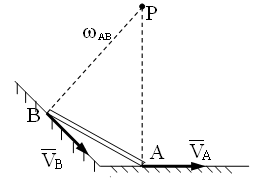 .Ц.С. находится на пересечении перпендикуляров к векторам скоростей точек. В этом случае по известной скорости одной из точек и ее расстоянию до М.Ц.С. сначала определяют угловую скорость и направление вращения фигуры, а затем определяют величину скорости другой точки и направление вектора скорости.

2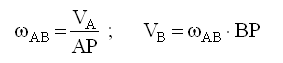 .Случай, когда векторы скоростей точек параллельны между собой и перпендикулярны отрезку,соединяющему точки

3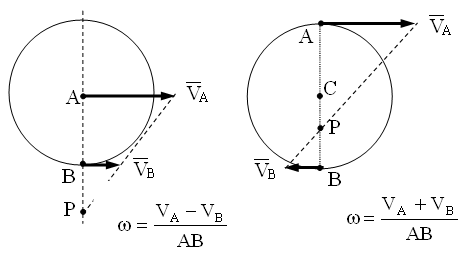 . Случай, когда векторы скоростей точек параллельны между собой и не перпендикулярны

отрезку,соединяющему точки.

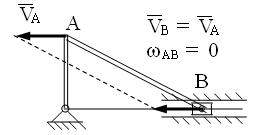В этом случае принято говорить о мгновенно поступательном движении тела. А это значит, что в данный момент движения фигуры (звена АВ).

1) угловая скорость тела равна нулю;

2) М.Ц.С. находится в бесконечности ;

3) скорости всех точек тела равны между собой.

Следует добавить также, что равенство скоростей наблюдается только в данный момент движения тела. Ускорения точек тела различны.