7. Как формулируется основная теорема статики о приведении системы сил к заданному центру?

Любую произвольную систему сил при приведении к некоторому центру приведения можно заменить одной силой, приложенной в центре приведения, и одной парой сил с моментом равным геометрической сумме моментов сил системы относительно центра приведения.Силу называют главным вектором системы сил, а вектор-ммент пары сил- главным моментом системы сил относительно центра приведения.

7. Что понимают под главным вектором и главным моментом системы сил? Как записывается это определение символами?

При упрощении ССС получается одна сила приложеная в центре приведения и равная векторной сумме сил системы. Эту силу называют главным вектором СС и обозначают При упрощении системы пар получается одна пара сил, вектор-момент которой, равен геометрической сумме векторов-моментов всех присоединённых пар а иначе геометрической сумме векторов-моментов всех сил системы относительно центра приведения. Вектор-момент такой пары сил называют главным моментом СС

~ где

5.9) Что понимается под главным вектором системы сил? Как определяются проекции этого вектора на оси координат?

Аналогично предыдущему вопросу. Плюс формулы:

5.10) Что понимается под главным моментом системы сил? Как определяются проекции этого вектора на оси координат?

Аналогично предыдущему вопросу. Плюс формулы:

6.1) На основании какой теоремы получают условия равновесия любой системы сил в векторной форме? Какой вид имеют эти условия?

На основании основной теоремы статики (теорема Пуансо): Любую произвольную систему сил при приведении к некоторому центру приведения можно заменить одной силой, приложенной в центре приведения, и одной парой сил с моментом равным геометрической сумме моментов сил системы относительно центра приведения.Силу называют главным вектором системы сил, а вектор-ммент пары сил- главным моментом системы сил относительно центра приведения.

6.2) Каковы векторные и аналитические условия равновесия произвольной пространственной системы сил?

Векторные:

Аналитические:

6.3) Каковы векторные и аналитичские условия равновесия произвольной плоской системы сил?

Векторные:

Аналитические: 1)

2)

3)

6.4) Каковы векторные и аналитические условия равновесия системы сил параллельной какой-либо из координатных осей?

Векторные ::

Аналитические:

Например параллельно оси Oz:

Плоскость yOz

6.5) Каковы три различных формы условий равновесия плоской системы сил? При решении каких задач они применяются?

Векторные:

Аналитические: 1)

2)

3)

При расчёте усилий в стержнях фермы, составных конструкций.

6.6) Как при приведении двух систем сил к одному центру определить — эквивалентны ли эти СС или не эквивалентны?

Две системы эквивалентны, если при приведении к одному центру равны их главные векторы и равны их главные моменты.

6.7) Чем отличаются понятия главный вектор системы сил и равнодействующая системы сил?

Равнодействующая приложена к точке пересечения линий действия всех сил системы, и равна их геметрической сумме, а главный вектор приложен в центре приведения и равен векторной сумме всех сил.

6.8) Как определить: приводится система сил к равнодействующей или к силовому винту?

1.

СС приводится к паре сил с вектором — моментом

2.

CC приводится к равнодействующей. R* проходит через центр приведения.

3.

СС приводится к равнодействующей. R* не проходитчерез центр проведения.

4.

Приводится к силовому винту.

6.9) Какая система сил называется силовым винтом? Как силовой винт можно заменить системой из 2 скрещивающихся сил?

Совокупность из силы и пары сил, расположенной в плоскости, перпендикулярной силе, называется силовым винтом или динамой.

Для получения скрешивающихся сил достаточно сложить главный вектор СС с одной из сил пары. Тогда получится, что ~

Величины сил и зависят от выбора плеча пары сил и оно может быть выбрано произвольно.

Всегда возможно приведение системы скрещивающихся сил обратно к силовому винту.

10. К 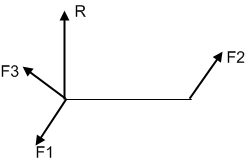акая величина называется векторным инвариантом СС? Что понимается под скалярным инвариантом системы сил?

Главныё вектор СС — векторный инвариант.

Скалярное произведение главного вектора и главного момента системы — скалярный инвариант.

7.1) Что понимается под центром параллельных сил? Запишите формулы для определения координат этой точки.

Центром параллельных сил называется геометрическая точка, через которую проходит линия действия равнодействующей системы параллельных сил, при любых поворотах линии действия сил системы относительно точек их приложения на одинаковый угол.

2. Какой вид имеет векторная формула для определения радиуса-вектора центра параллельных сил?

2. Какой вид имеют интегралы для определения координат центра тяжести однородных объёмных тел, плоских пластин и тяжёлых линий?

2. Какие вспомогательные теоремы позволяют определить координаты центров тяжести однородных геометрических тел?

Если однородное тело имеет плоскость (ось или центр) симметрии, то центр тяжести тела находится в этой плоскости (на этой оси или в этом центре) симметрии.

2. Как формулируются теоремы Гульдина-Паппа для определения поверхностей и объёмов тел вращения?

Площадь боковой поверхности фигуры, образованной вращением плоской линии относительно оси, находящейся в плоскости линии и не пересекающей её, равна произведению длины линии на длину окружности, описанной центром тяжести этой линии.

Объём тела, полученного вращением плоской фигуры относительно оси, находящейся в плоскости фигуры и не пересекающей её, равен произведению площади фигуры на длину окружности, описанной центром тяжести этой фигуры.

2. Какой вид имеет формула для определения координаты центра тяжести дуги радиуса R с центральным углом 2α?

2. Какой вид имеет формула для определения координаты центра тяжести сектора круга радиуса R и с центральным углом 2α?

2. Какие два основных способоа определения координат центров тяжести тел при решении задач? Покажите из на простом примере.

С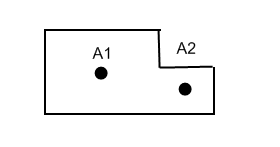 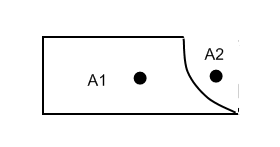пособ расчленения и дополнения:

2. Какой вид имеют формулы для определения координат центров тяжестей однородных плоских пластин, объёмных тел и тяжёлых линий?

2. Что понимается под статическими моментами площади плоской фигуры относительно осей? Как определить их величины?

Под статическим моментом площади плоской фигуры относительно некоторой оси понимается сумма произведений элементарных площадок, из которых состоит фигура, на расстояния центров тяжести этих площадок до этой оси.

1. Какая конструкция называется фермой? По какой формуле определяется число стержей статически опреелимой фермы?

Под фермой понимают жёсткую неизменяемую конструкцию, состоящую из стержней и соединяющих их шарниров.

2. Какие три основных допущения используются при определении усилий в стержнях плоских и пространственных ферм?

1) Стержни фермы считаются невесомыми;

2) Шарниры, соединяющие стержни между собой считаются идеальнымыми, то есть без трения;

3) Силы, действующие на фермы, считаются приложенными только в узлах фермы — то есть в связывающих стержни шарнирах.

3. С чего начинается расчёт любой фермы? Как при расчётах учитывается вес стержней фермы?

Расчёт фермы всегда начинается с определения неизвестных сил реакций связей фермы в её опорных узлах. Затем составляется 3 уравнения равновесия для системы всех внешних сил, действующих на рассматриваемую ферму. Отсюда определяются реакции в опорных узлах, а затем приступают к определению усилий в стержнях фермы. Вес не учитывается.

4. В чём сущность метода вырезания узлов при определении усилий в стержнях ферм?

В определённой последовательности рассматриваются сходящиеся системы сил, действующих на каждый из узлов фермы. Для каждого узла составляется 2 уравнения равновесия в проекциях сил на оси координат. Из уравнений определяются усилия в требуемых стержнях.

5. В чём сущность метода сечений (метода Риттера) при определнии усилий в стержнях ферм?

Ферма мысленно (а на расчётной схеме видимой чертой) рассекается на 2 части. Действие перерезаемых стержней на части фермы, заменяется силами. Из уравнений равновесия для системы известных и трёх неизвестных сил, действующих на одну из частей фермы, определяются неизвестные усилия в перерезаемых стержнях.

6. Какие три формы условий равновесия плоской СС используются при определении усилий в стержнях фермы методом сечений?

1)

2)

3) Либо уравнение проекций сил на ось, перпендикулярную линиям действия двух неизвестных сил (когда пояса фермы параллельны), либо уравнение моментов сил относительно третьей точки пересечения линий действия неизвестных сил.

7. Какое существует правило для направления усилий в рассекаемых стержнях? Как заием определяют - сжат стержень или растянут?

Изображая силы, действующие со стороны стержней на рассматриваемый узел, векторы усилий направляют от узла, считая стержни фермы растянутыми. Знак — стержень сжат, + растянут.

8. Какие леммы без расчётов позволяют определить усилия в отдельных стержнях ферм?

1) Если в ненагруженном узле фермы сходятся 2 стержня то усилия в каждом равны нулю.

2) Если в узле сходятся 2 стержня, а действующая на узел сила направлена вдоль одного из стержней, то усилие во втором равно нулю.

3) Если в ненагруженном узле фермы сходятся 3 стержня и два из них расположены на одной прямой, то усилия в упомянутых стержнях между собой равны, а усилие в третьем стержне равно 0.

8.9) Какие точки называются точками Риттера при определении усилий в стержнях ферм методом сечений?

Точки, в которых пересекаются линии действия двух из трёх неизвестных сил.

10. В чём сущность графического способа определения усилий в стержнях ферм с помощбю диаграмм Максвелла-Кремоны?

Точное построение по определённым правилам диаграммы из замкнутых векторных многоугольниклв сил, действующих на каждый узел фермы, измерение сторон этих многоугольников, определение усилий в стержнях по принятому масштабу изображаемых сил.

1. Чем отличается реакция негладкой поверхности по величине и направлению от реакции гладкой поверхности?

Реакция негладкой поверхности это совокупность силы трения и силы нормальной реакции плоскости, на которой располоено тело. Из-за этого вектор полной реакции шёроховатой поверхности образует с нормалью к поверхности некий угол φ, который при принято называть углом трения. В гладкой поверхности силы трения отсутствуют.

2. В каких пределах может изменяться сила трения при равновесии тела? Как определяется максимальная величина силы трения?

От 0 до максимального значения.

3. От чего зависит величина коэффициента трения скольжения (коэффициента сцепления) тела на негладкой поверхности?

От материала соприкасающихся тел и от качества обработки поверхности

4. Что понимается под вектором полной реакции шероховатой поверхности? Как определяется модуль этого вектора?

Реакция негладкой поверхности это совокупность силы трения и силы нормальной реакции плоскости, на которой располоено тело. Из-за этого вектор полной реакции шёроховатой поверхности образует с нормалью к поверхности некий угол φ, который при принято называть углом трения.

1. Что понимается под углом трения и под конусом трения? Чему равен тангенс угла трения?

Угол φ, который вектор полной реакции шёроховатой поверхности образует с нормалью к поверхности, который при принято называть углом трения. Конус трения — является геометрическим местом всех возможных реакций шёроховатой поверхности. Угол трения — угол, тангенс которого равен коэффициенту трения

2. При каком максимальном угле наклона плоскости к горизонту тело при наличии трения будет двигаться вдоль плоскости?

При угле наклона плоскости большем чем угол трения.

3. По какой причине возникает сопротивление качению тяжёлого тела по плоскости? Чему равен момент сопроивления качению?

Так как плоскость под тяжёлым телом деформируется.

4. Чему равен главный вектор и главный момент системы сил реакций шероховатой поверхности при качении по ней тяжёлого катка?

5. Каковы размерности коэффициентов трения качения и скольжения? От чего зависят эти величины?

Они безразмерны. Зависят от материалов соприкасающихся тел и качества их обработки

6. Что понимается под коэффициентом устойчивости в задачах на устойчивость тел и механизмов?

Отношение

КИНЕМАТИКА

1. Что понимается под системой отсчёта и какая система отсчёта в классической механике считается основной?

Под системой отсчёта понимают тело, относительно которого рассматривается движение, связанную с телом систему координат и систему счисления времени. Неподвижная система отсчёта считается основной.

2. Что значит - «задать движение точки»?

Задать уравнение движения точки в заданной системе координат.

3. Какие способы задания движения точки используются при описании движения и при решении задач?

Векторный координатный и естесственный

4. Что понимается под годографом переменного вектора?

Годографом вектора называется линия, которую описывает конец переменного вектора, начало которого совмещено снеподвижной точкой.

5. Каков физический смысл производной по времени от любого переменного вектора?

Производная по времени от любого переменного вектора — это вектор, направленный по касательной к годографу дифференцируемого вектора и равный скорости движения конца вектора по его годографу.

6. Какой вид имеет годограф единичного вектора вращающегося относительно неподвижной оси системы координат?

Окружность

7. Какой вид имеют параметрические уравнения годографа радиуса-вектора точки?

8. Какой вид имеет годограф вектора скорости точки при её прямолинейном движении?

Прямая

9. Какой вид имеет годограф вектора скорости точки при её равномерном движении по окружности?

Окружность

10. Какой вектор направлен по касательной к годографу вектора скорости точки?

Ускорение

1. Как определяются векторы скорости и ускорения точки при векторном способе задания её движения?

Скорость — производная по времени от радиуса-вектора движущейся точки.

Ускорение — вторая производная по времени от радиуса-вектора движущейся точки

2. Как по величине и по направлению определяются векторы скорости и ускорения точки при координатном способе задания движения?

3. Что задаётся при естесственном способе задания движения точки?

Зависимость дуговой координаты от времени.

4. Как выводится формула для определения вектора скорости точки при естесственном способе задания движения?

Дифференцируя как сложную функцию по времени получим: v

5. Как выводится формула для определения ускорения точки при естесственном способе задания её движения?

6. Как определяется по величине и что характеризует и как направлено касательное ускорение точки?

Касательное ускорение характеризует изменение величины скорости и направлено по касательной к траектории точки

7. Как определяется по величине что характеризует и как направлено нормальное ускорение точки?

Нормальное ускорение характеризует изменение направления вектора скорости точки, и направлено к центру кривизны траектории точки.

8. Как образуется подвижный трёхгранник и естесственные оси координат?

Одна из осей направляется по касательной к траектории движущейся точки, другая ось к центру кривизны траектории точки, третья направляется так, как направлена ось Z по отношеннию к осям X и Y.

9. Как называется и как направлено ускорение, определяемое из формулы

Касательное ускорение; по касательной к траектории точки

10. Как называется и как направлено ускорение, определяемое из выражения

Нормальное ускорение; к центру кривизны траектории точки

3.1. Как перейти от векторного способа задания движения к координатному?

вектор скорости точки, и вектор ее ускорения при координатном способе задания движения определяются через их проекции на координатные оси. А как найти модуль каждого вектора и его направляющие косинусы, повторять, наверное, не стоит.

При координатном способе задания движения:

r = i×x + j×y + k×z ,

где x, y, и z - координаты точки, являющиеся некоторыми

функциями времени.

I j k — векторы -орты

3.2)коордиатный в естесственный

1. Определение радиуса кривизны — исключить из уравнений параметр t

2. Определение закона движения

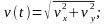
3. Определение V; a; ; ;

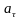33)

3. Как направляется вектор-орт при естественном способе задания движения?