Правило развертывания

Это правило определяет действие обратное склеиванию.

Правило развертывания элементарного произведения в логическую сумму элементарных произведений большего ранга (в пределе до r = n, т.е. до конституент единицы, как и будет рассмотрено ниже) следует из законов универсального множества, распределительного закона первого рода и производится в три этапа:

- в развертываемое элементарное произведение ранга r вводится в качестве сомножителей n-r единиц, где n- ранг конституенты единицы;

- каждая единица заменяется логической суммой некоторой, не имеющейся в исходном элементарном произведении переменной и ее отрицания: x_i v x_i = 1;

- производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходного элементарного произведения ранга r в логическую сумму 2^n-r конституент единицы.

66. Полная система в алгебре логики

Множество функций алгебры логики A называется полной системой (в P2), если любую функцию алгебры логики можно выразить формулой над A.

67. Минимальный базис

Минимальным базисом называется такой базис, для которого удаление хотя бы одной функции f₁ , образующей этот базис, превращает систему функций (f₁, f₁,…, f_m) в неполную.

68. Перечислите примеры полных систем

1) {V, ¬} ;

2) {&, ¬} ;

3) { | };

4) {&, ⊕ , 1}базис Жегалкина.

69. Алгебра Жегалкина

Множество булевых функций, заданных в базисе Жегалкина S4={⊕,&,1} называется алгеброй Жегалкина.

70. Полином Жегалкина

Полиномом Жегалкина (полиномом по модулю 2) от n переменных x₁,x₂ ... x_n называется выражение вида:

c₀⊕c₁x₁⊕c₂x₂⊕ ... ⊕c_nx_n⊕c₁₂x₁x₂⊕ ... ⊕c_12 ... nx₁x₂ ... x_n,

где постоянные C_k могут принимать значения 0 ли 1.

Тип 2 (развернутый ответ)

НАСТЯ ВЕРЕНИЧ:

1. Понятие примитивно-рекурсивых функций

2. Примеры примитивно-рекурсивых функций

3. Примеры примитивно-рекурсивых операторов

4. Схемная интерпретация примитивной рекурсии

5. Частично рекурсивные и общерекурсивные функции

6. Ассоциативное исчисление-cовокупность символов в заданном алфавите вместе с системой подстановок. пусть имеется алфавит, составл.символы-буквы.Любая конечная последовательность букв-слово. Рассмотрим 2 слова N,Mв нек.алфавите А. Если Nявл.частью M,то говорят,что Nвходит вM. Зададим в нек.алфавите конечную сист.подстановок. N-M, S-T, гдеN,M,S,T-слова в алфавите А. Любую подстановку N-Mможно применить к слову Kслед.образом. Если в Kимеется одно или несколько вхожд.в слово N, то любое из них может быть заменено словом М,и наоборот,если имеется вхожд.в слово М,то его можно заменить на N.

7. Норм. Алг. Маркова-1)пусть задан алф.А и сист.подстановок В 2)для произвольного слова Р подстановки из В выбир.в том же порядке,в кот-ом следуют в В. 3)если подход.подстановки нет процесс останавл. 4)в противн. Случае берется первая из подход.подстановок и происх.замена ее правой частью первого из вхожд.левой части В 5)все действия повторяются для полувшегося слова Р₁ 6)если примен.последн.подстановка из В процесс останавливается.

Норм.алгоритм. можно рассматривать как универсальную форму. Принцип: для алг. В произ.конечном алфавите А можно построить норм.эквив.ему алгоритм. Алг.для кот-го можно построить норм алг. Будет нормализуемым. Все алг.в конечном алф.А нормализуемы.

8. Способы композиции нормальных алгоритмов- композ-я позволяет строить новые алгоритмы из известных, не выходя за границы класса норм.алгоритмов. Способы композиции:1)суперпозиция алгоритмов А В: вых.слово алг.А рассматривается как вх.слово для алг.В.И общ.алг. С(P)=B(A(P))

2)Объедин.алг. А и Б в одном и том же алфавите есть алг. С в том же алфавите. Преобраз слово Р,находящееся в области определения и алг.А и алг.В в записанные рядом слова А(Р) и В(Р).

3)разветвление алг. Представляет собой композицию Д трех алгоритмов А,В, и С. Причем область опред.алг. Д есть пересечение областей алгоритмов А,В,С. Для любого слова Р Д(Р) есть А(Р),если С(Р)=е, где е –пустая строка, или равно В(Р) в противн.случае.

4)Итерация алгоритмов.Такая композиция С алгоритмов А и В, что для вх.слова Р результат С(Р) получ.после последовательного многократн.повторения алг.А до тех пор, пока не получается слово преобразуемое алг.В.

9. Понятие алгебры, ее элементы, подалгебра–фун-ии типа Мⁿ M будем наз-ть n-арной операцией на множ-ве M.множ-во М вместе с заданной на нем совокупностью оп-ий О={ ₁, _{2… n}} есть алгебра А={M; _{1, 2… n}}.вектор (n₁,n₂...n_m) артностей операций,где n_i- артность _i.Сигнатура алгебры- совокупность операций O={ ₁, ₂… _n). Множ-во N’ 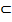M наз-ся замкнутным относит-но опер-ии , если (M’ⁿ)=M’.Если множ-во M’= (M’ⁿ) замкнуто относительно всех оп-ий алг.А,тогда A^’={M’, _{1, 2}… _n} подалгебра А.

10. Свойства бинарных алгебраических операций- 1)Ассоциативная бинарная операция-оп-ия - ассоциативная, если можем ставить скобки произв.образом или не ставить вообще. a b c=a (b c) 2)Коммутативная бинарная операция-оп-ия комм., если a b=b a 3)Бинарная операция, дистрибутивная слева и справа-оп-ия дистрибутивна слева относит. оп-ии , если для abc вып.рав-во a (b c)=a b a c(*,+)(*,-). Оп-ия -дистрибут.справа отосит-но оп-ии , если вып. a b c=a b c(/,+)(/,-)(*,+)(*,-).

НАСТЯ НАГОРНАЯ: