Контрольная работа по курсу «Математическая логика и теория алгоритмов» модуль 2

Структура варианта контрольной работы:

4 вопроса типа 1 (7 х 1 балл) + 1 вопроса типа 2 (1 х 3 балла) = 10 баллов

Длительность работы – 45 минут.

Вопросы к контрольной работе:

Тип 1 (краткий ответ)

1. Функция следования

f(X)=x+1 примитивно рекурсивная функция является объектомбазиса , так же как и константа 0 используются – для включения ряда натуральных чисел в базис.

2. Функции тождества в базисе примитивной рекурсии

( (x1,..xi,..xn),m*n) – является объектом базиса, семейство функций или функции введения фиктивных переменных (x1,..xi,..xn)= – все переменные кроме xm – являются фиктивными,незначащими.

3. Перечислите объекты базиса примитивной рекурсии

Объекты базиса: это примитивно рекурсивные функции такие как

Все члены ряда натуральных чисел, функции следования, константа ноль, семейство функций тождества.

4. Оператор суперпозиции

(g,h,..,hn) – оператор суперпозиции, задает подстановку в функцию м одних переменных м от других н, где h(x) – функция куда подставляют,g1(x1,..,xm),..,gn(x1n,..,xm) функции. Пусть есть тогда функция = ( )

5. Оператор примитивной рекурсии

Оператор примитивной рекурсии fi(x1,..,xn)

fi(x1,..,xn) =  =

6. Перечислите действия в определении примитивной рекурсии

Семейство операторов суперпозиции, Оператор примитивнойрекурсии

7. Схема примитивной рекурсии

F(x1,..,xn,0)=g(x1,..,xn) and F(x1,..,xn,y+1)=f(x1,..,xn,y,f(x1,..,xn,y))

F(0)=candf(y+1)=f(y,f(y)) – преобразованная схема.

8. Оператор минимизации функции по переменной

Пусть имеется функция:f(x1,..,xn) операция миним-ии обозначается:

U( )=xi

)– решается подбором(1-левая часть не определена, поэтому на я минимизации не определена. 2- на каждом шагеоперация не определена но не для каждого значения оно не выполняется. 3-левая часть равенства определена на всех у y<=z,y<z – не выполняется, y=z – выполняется, в этом случае z – результат минимизации функ-ии по i-ой переменной)

9. Частично-рекурсивная функция

Функция которая может быть построена из 0, функций следования, функций тождества, путем конечного применения операторов суперпозиции ,примитивной рекурсии, u – операторов – называют частично рекурсивной(f(x1,..,xn)=uy(g(x1,..,xn-1,y)=xn)).

10. Общерекурсивная функция

Если функция определена на всех наборах х она называется обещерекурсивной(обратная к x+1=uy(y+1-x) не определена при х=0).

11. Смежные слова в ассоциативном исчислении

Два слова p1 и p2 в ассоциативном исчислении называются смежными, если одно изних может быть получено из другого однократным применением дополнительной подстановки

12. Дедуктивная цепочка в ассоциативном исчислении

Последовательность слов P1,..,Pn – называется дедуктивной цепочкой если каждое из двух слов в паре смежные

13. Эквивалентные слова в ассоциативном исчислении

Слова P ,M – эквивалентные если существует цепочка от P ,M и обратно

14. Суперпозиция нормальных алгоритмов

Суперпозиция алгоритмов – способы композиции алгоритмов(A,B – выходные слова, рассматривается как входное слово для Б, C(p)=B(A(p)))

15. Объединение нормальных алгоритмов

Объединение алгоритмов – А и Б в одном и том же слове – есть алгоритм С-в том же алфавите, преобразующей любое слово, лежащее в области определения и алгоритма А и алгоритма Б в записанные слова

16. Разветвление нормальных алгоритмов

Разветвление алгоритмов представляет собой композицию 3-ех алгоритмов А,Б,С. Д – пересечение областей определения алгоритмов А,Б,С. Для любой общ. обл. определения Д(р)=А(р), если С(р)=е – где –пустая строка для Д(р), в противном случае: Д(р)=А(р) – С(р)=е иначеД(р)=Б(р)

17. Итерация нормальных алгоритмов

Итерация – это такая композиция С – алгоритмов А и Б, что для любого р – результат С(р) – получается после последовательного многократного повторения алгоритма А – до тех пор, пока не получится слово преобразуемое алгоритмом Б

18. Логика- наука, изучающая методы установления истинности или ложности высказываний, утверждений на основе истинности или ложности других.

19. Цель математической логики-исследование алгоритмических процессов с заданными свойствами, нахождение взаимосвязей между доказуемостью, истинностью и вычислимостью.

20. Высказывание- предложение , относительно которого можно четко сказать истинно оно, или ложно.

21. Перечислите основные логические связки (операции)- конъюнкция(и,&); дизъюнкция(или,+); инверсия(не, ); импликация(если то, ); неравнозначность(либо либо, ); эквивалентность(если и только если, );

22. Таблица истинности дизъюнкции(1+1=1; 1+0=1;0+1=1;0+0=0)

23. Таблица истинности конъюнкции(1*1=1;1*0=0;0*1=0;0*0=0)

24. Таблица истинности импликации(0 0=1; 0 1=1; 1 0=0; 1 =1)

25. Таблица истинности эквивалентности(1 1=1; 1 0=0;0 1=0;0 =1)

26. Таблица истинности неравнозначности(1 1=0;1 0=1;0 1=1;0 0=0)

27. Порядок выполнения логических операций-1)то что в скобк.2)при отсутствии 1-отрицание,2-конъюнк.3-дизъюнк. и потом все остальное

28. Понятие алгебры-множ-во М вместе с заданной на нем совокупностью оп-ий О={ ₁, _{2… n}} есть алгебра А={M; _{1, 2… n}}

29. Носитель алгебры- пусть A={R,+,*} R-носитель

30. Тип алгебры- вектор (n₁,n₂...n_m) артностей операций,где n_i- артность _i.

31. Сигнатура алгебры- совокупность операций O={ ₁, ₂… _n)

32. Подалгебра-если множ-во M’= (M’ⁿ) замкнуто относительно всех оп-ий алг.А,тогда A^’={M’, _{1, 2}… _n} подалгебра А.

33. Ассоциативная бинарная операция-оп-ия - ассоциативная, если можем ставить скобки произв.образом или не ставить вообще. a b c=a (b c)

34. Коммутативная бинарная операция-оп-ия комм., если a b=b a

35. Бинарная операция, дистрибутивная слева и справа-оп-ия дистрибутивна слева относит. оп-ии , если для abcвып.рав-во a (b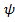 c)=a b a c(*,+)(*,-). Оп-ия -дистрибут.справа отосит-но оп-ии , если вып. a b c=a b c(/,+)(/,-)(*,+)(*,-)

36. Логическая переменная

переменная, которая может принимать только два значения : 0 или 1(false, true)

37. Логическая функция

это функция логических переменных, которая может принимать только два значения : 0 или 1(false, true)

38. Булева алгебра

раздел математической логики, изучающий высказывания и операции над ними. Наиболее известными операциями булевой алгебры являются: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание; тип алгебры, в которой все переменные и функции могут принимать только два значения: 0 и 1.

39. Фиктивная переменная в логической функции

переменная, от которой не зависит значение функции(то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает)

40. Логические функции одной переменной

таблица истинности функции одной переменной Y=f(X) содержит всего 2 строки, а число функций одной переменной равно 4. Это фунции: 1Функция константа 0, Y=0; 2 Функция Y=f(X)=X — функция повторения; 3 Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия; 4 Функция константа 1, Y=1

41. Формула

выражение в языке формальной логики, являющееся аналогом предложения. С помощью логических переменных и символов логических операций ею можно заменить (формализовать) любое высказывание

42. Глубина формулы

Sum=(f1,..,fn), x1,..,xn – формулы глубины, F-имеет глубину r+1, если она представляет собой функцию f(F1,..,Fni) ,где fisum ni- арность – число аргументов. Fj – формула максимальная глубина которых равна к . Fj- подформулы формулы F. Все подформулы для Fj – являются подформулами для F.

43. Эквивалентные формулы

Формулы A₁, A₂ – называются равносильными или эквивалентными, если для любого набора значений аргументов x₁, x₂,…,x_n, они принимают одинаковые значения. (это формула, которая принимает значение истины или лжи одновременно с исходной)

44. Способы доказательства равносильности формул

1. C помощью таблицы истинности. 2. Путем рассуждения

45. Формула разложения функции от n переменных по mпеременным

В общем виде для функции f(x₁,x₂,..,x_n) от n переменных разложение по m переменным (mn) имеет вид

где дизъюнкция берется по всем 2^m наборам переменных x₁,x₂,..,x_m

46. Совершенная дизъюнктивная нормальная форма

формулаf=D1˅D2˅…˅Dm, где всеD_iявляются основными элементарными конъюнкциями

47. Алгоритм построения СДНФ

СДНФ функции f содержит ровно столько конъюнкций, сколько единиц в таблице истинности f; каждому “единичному” набору (d ₁,…,d _n), т.е. набору, на котором значение функции равно 1, соответствует конъюнкция всех переменных, в которой x_i взято с отрицанием, если d i=0, и без отрицания, если d _i=1

Пример 5.1. Записать СДНФ для функции x₁  x₂.

x1 x2	x1  x2	Основная элементарная конъюнкция
0 0	1
0 1	1	x2
1 0	0
1 1	1	x1x2

.