8. Межі зміни цін на продукцію, для яких структура плану початкової задачі не змінюється.

Рентабельна продукція — А і С. Для А(х₁):

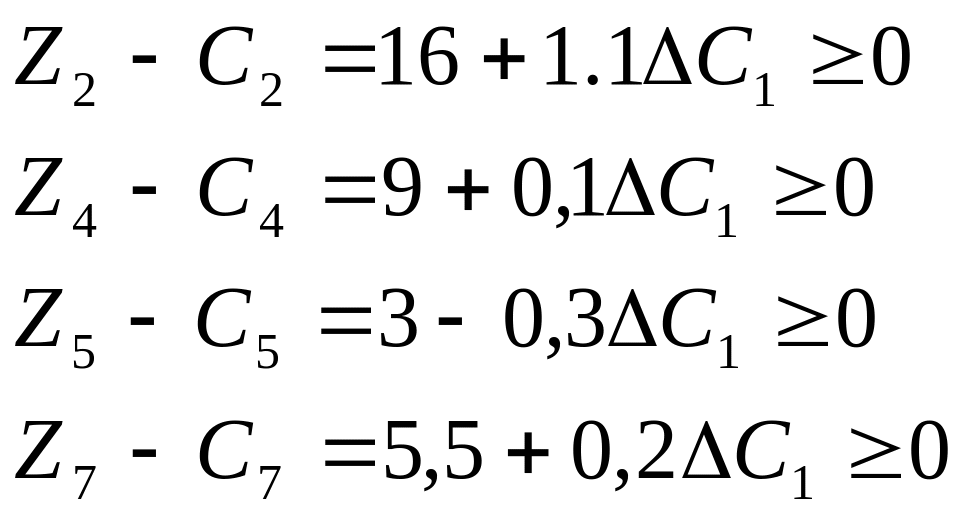
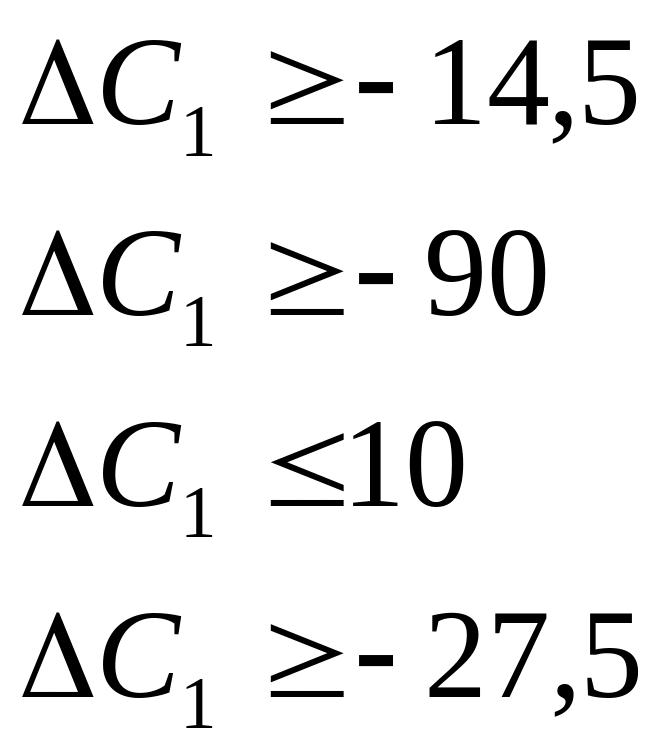
Для С(х₃):

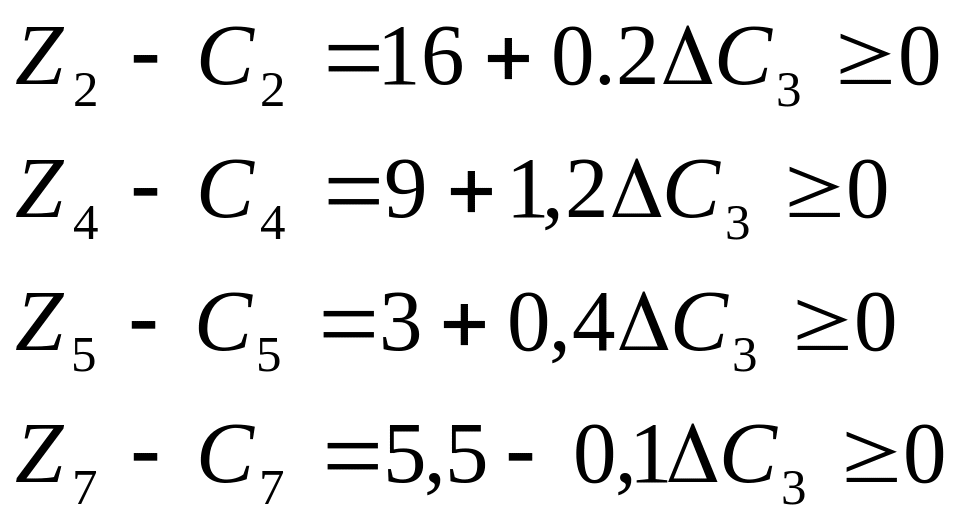
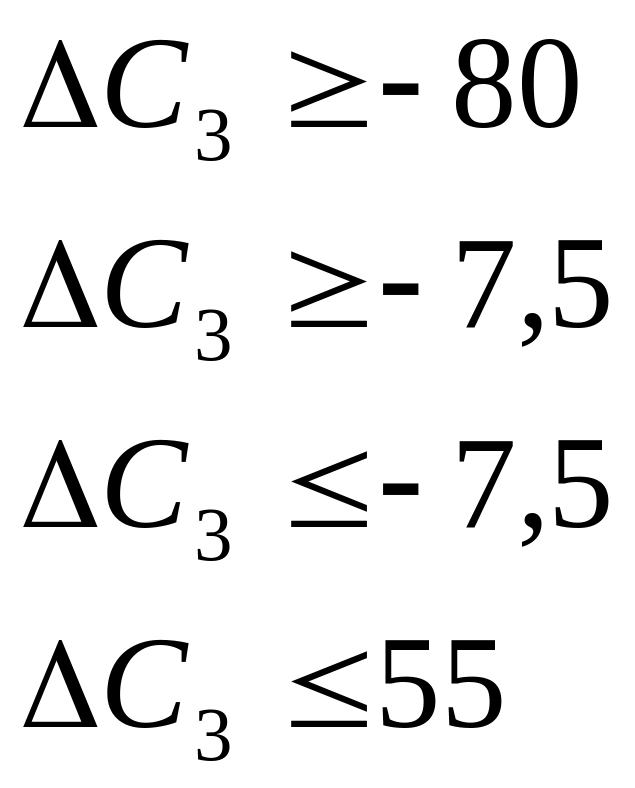
Отже, ціна на продукцію А може коливатися в межах , а прибуток . Ціна на продукцію С може коливатися , а прибуток .

9. Доцільність розширення асортименту продукції за рахунок включення в план виробництва нового виду продукції.

Е= ;С₅=52

4*3+5,5*8=56>52, отже вводити нову продукцію не вигідно, так як вона є збитковою.

ІІчастина

1. Постановка завдання.

1. Побудувати математичні моделі початкової та двоїстої задач.

2. Знайти оптимальні плани обох спряжених задач.

3. Дати економічне тлумачення основним і додатковим змінним початкової і двоїстої задач та значенням їхніх цільових функцій.

4. Визначити дефіцитні та недефіцитні ресурси.

5. Визначити рентабельні та нерентабельні види продукції.

6. Знайти межі зміни обсягів виробничих ресурсів, для яких змінні двоїстої задачі лишаються незмінними.

7. Знайти межі зміни цін на продукцію, для яких структура плану початкової задачі не змінюється

8. Проаналізувати доцільність розширення асортименту продукції за рахунок включення в план виробництва нового виду продукції.

2. Математичні моделі початкової та двоїстої задач.

Початкова задача:

Z=50x₁+48x₂+45x₃+50x₄(max)

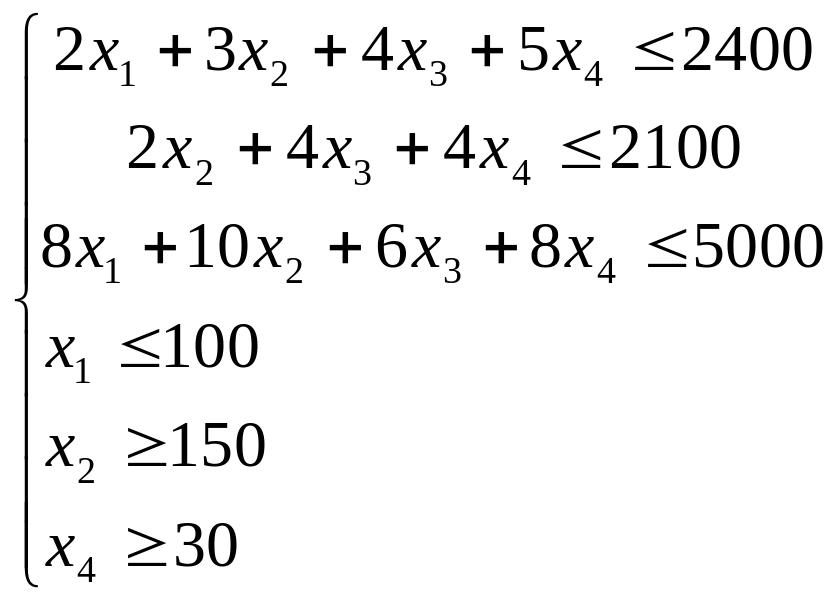
Двоїста задача:

F=2400y₁+2100y₂+5000y₃ +100y₄-150y₅-30y₆(min)

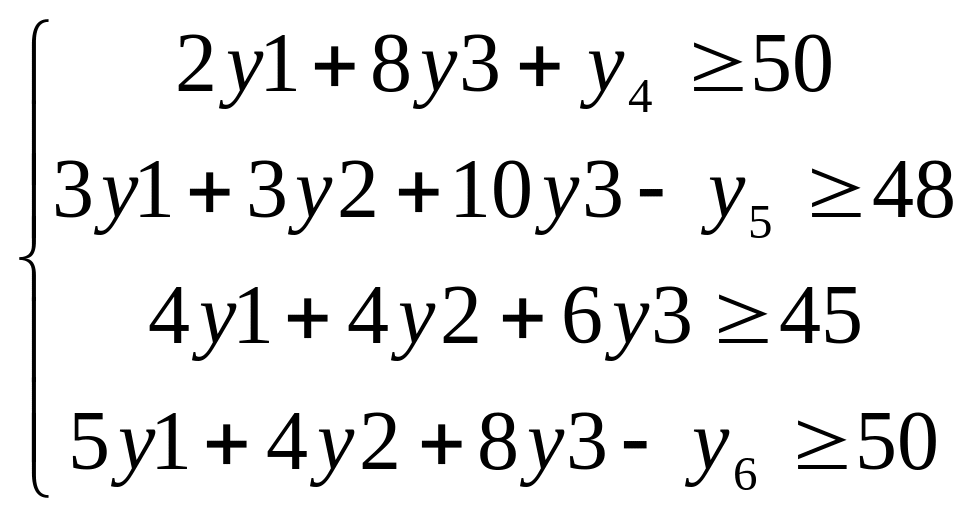
3. Оптимальні плани обох спряжених задач.

Початкова(остання симплекс таблиця):

i	Cб	xб	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10	A11	A12
1	0	x5	70	0	0	0	0	1	-1	0	-2	0	1	0	-1
2	-M	x9	30	0	0	0	0	0	-0.27	0.18	-1.45	1	0.36	-1	-0.36
3	50	x1	100	1	0	0	0	0	0	0	1	0	0	0	0
4	45	x3	360	0	0	1	0	0	0.45	-0.14	1.09	0	0.73	0	-0.73
5	48	x2	180	0	1	0	0	0	-0.27	0.18	-1.45	0	0.36	0	-0.36
6	50	x4	30	0	0	0	1	0	0	0	0	0	-1	0	1
Zj-Cj≥0			31340	0	0	0	0	0	7.36	2.59	29.27	0	0.18	M	-0.18+M
								Y1	Y2	Y3	Y4	Y5	Y6

Xопт=(100;180;360;30)

Z=50*100+48*180+45*360+50*30=31340

Перевірка в MS Excel:

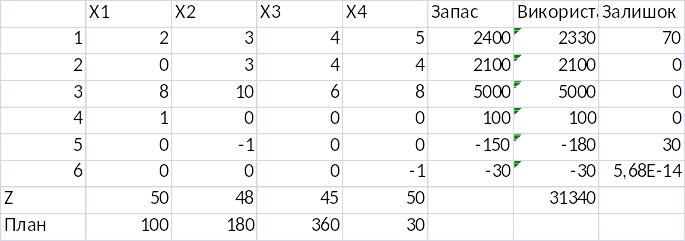
Двоїста:

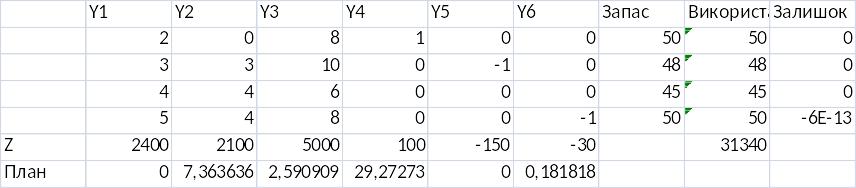
Zmax=Fmin