14. Обработка результатов прямых многократных измерений. Идентификация закона распределения результатов измерений. Составной критерий.

При статистической обработке результатов прямых многократных наблюдений выполняют исключение грубых промахов, систематических погрешностей из результатов наблюдений и вычисляют показатели точности.За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки исключающие систематические погрешности. Поправки определяют экспериментально при калибровке средств измерений или по результатам специальных исследований. При обработке необходимо определить оптимальное число поправок, которые следует вводить в результаты наблюдений для получения более достоверных сведений об истинном значении измеряемой величины.

Оценка СКО результата наблюдения. Несмещенной, состоятельной, эффективной оценкой для генерального среднего 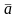нормального распределения является выборочное среднее , определяемое по формуле

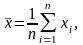(1) где x₁, x₂, ... x_n – совокупность значений случайных величин x.

Несмещенную оценку среднего квадратического отклонения (СКО)  для n > 60 определяют по формуле

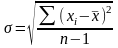, если  неизвестно, и 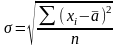,если  известно.

Для n < 60 несмещенную оценку СКО получают путем умножения  на коэффициент M_к, значение которого изменяется в диапазоне от 1,25 до 1,00 соответственно при n = 2 и n = 60 .

СКО результата измерения оценивают по формуле

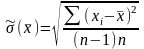,где 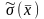– оценка СКО результата измерения; – результат измерения (среднее арифметическое исправленных результатов наблюдений); х_i – i-й результат наблюдений.

Невесь!!

14. Обработка результатов косвенных измерений. Случайные и систематические погрешности косвенных измерений.

В результате косвенных измерении определяется значение физической величины, связанной с другими z=f(a₁,a₂,...a_m). Пусть каждая из вел-н а_j измерена с погрешностью Δа_j. Нужно оценить зн-ие погрешности Δz результата косвенных измерений.

Рассматривая как функцию m переменных а_j запишем полный дифференциал dz=Σ(ðf/ðа_j)da_j (1) ->Δz= Σ(ðf/ðа_j)Δa_j (2), где ðf/ðа_j – коэффициент влияния соответствующей погрешности Δa_j. (ðf/ðа_j)Δa_j – частная погрешность, доля общей погрешности Δz.

Если известны систематические погрешности Δa_j результата прямых измерений величин a_j, то по (2) вычисляем систематическую погрешность Δz. Если (ðf/ðа_j)Δa_j имеют разные знаки, то происходит частичная компенсация погрешностей.

Оценивание случайной погрешности результатов косвенных измерений. Пусть a_j измерены со случайными погрешностями Δj , имеющими нулевые математические ожидания М[Δj]=0 и дисперсии σ_j². Используя (2) запишем выр-ие для дисперсии погрешности Δz, если Δj некоррелированы σ²[Δz]= Σ(ðf/ðа_j)²σ_j² (3)

14. Обработка результатов совместных измерений. Метод наименьших квадратов.

Совместные измерения в промыслово-геофизической практике применяют при исследовании петрофизических связей, градуировке геофизической аппаратуры и т.д. Порядок реализации: выполнение определенного числа измерений для получения результатов с заданной вероятностью, исключение грубых промахов, графическое представление результатов измерений с оценкой характера погрешностей, составление уравнения номинальной градуировочной характеристики средства измерения, исследование состава погрешности средства измерения, расчет основных метрологических характеристик.

МНК выполняет статистическую обработку результатов совместных измерений. Суть метода - экспериментатор имеет возможность заранее выбрать значение входной величины x или изменять (регулировать) входную величину так, чтобы установить прибор на отметку х. При фиксированной входной величине х измеряется соответствующее значение выходной величины у. При использовании метода наименьших квадратов коэффициенты у₀ и S градуировочной характеристики находят из условия минимума взвешенной суммы квадратов отклонений экспериментальных точек от прямой

у = у₀+Sх.(1) Коэффициенты линейной регрессии: чувствительность S и нуль-сигнал аппаратуры у₀, либо аддитивную составляющую систематической погрешности измерений, получают по следующим формулам: 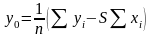;(2)

Коэффициенты параболической регрессии по методу наименьших квадратов определяют из системы уравнений :

 aA₄ + bA₃ + cA₂ = B₁

 aA₃ + bA₂ + cA₁ = B₂

 aA₂ + bA₁ + c = B_3, где ; ; ; ;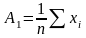

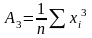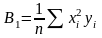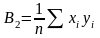; ; .-> y = ax² + bx + c.(4) Градуировочные характеристики в виде уравнений (1, 4) считают номинальными.