11. Грубые погрешности и методы их исключения. Критерии исключения грубых погрешностей. Критерии “трех сигм”, Романовского, Шовенэ.

Грубые погрешности (промахи) возникают из-за ошибок или неправильных действий оператора, а также при кратковременных, резких изменениях условий проведения измерений (сбои в работе прибора, удары прибора о стенки скважины и т.п.).

Если грубые погрешности и промахи обнаруживают в процессе измерений, то результаты, содержащие их, отбрасывают. При проведении ряда одинаковых измерений всегда будет некоторый разброс его результатов. При этом могут встретиться измерения с большими случайными ошибками, которые являются естественными статистическими отклонениями. Их незаконное отбрасывание (считая их промахами) может необоснованно завысить и сделать фиктивной точность всего ряда измерений.. Поэтому в процессе обработки результатов наблюдений промахи надо выявлять и исключать из дальнейшего анализа.

Наиболее простой способ исключения грубых ошибок х_k основан на том, что вероятность появления значения, уклоняющегося от среднего арифметического более чем на 3, равна 0,003, и поэтому результаты, вероятность получения которых меньше 0,003, можно считать промахом. В некоторые виды задач вводят условие исключения результата, у которого |_i|>2. При этом 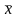и  вычисляют по формулам, в которые не входит значение х_k. Поэтому число всех измерений равно n-1. Результат измерения х_k должен быть отброшен, если (х_k - ) > 3.

Однако вследствие того, что рассчитывают не , а 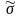, а также в тех случаях, когда грубый промах не один, а их несколько, а также при небольшом числе измерений критерий 3 ненадежен.

Если распределение погрешностей измерений можно считать нормальным, то грубые промахи исключают, основываясь на критериях Шовине, Романовского, Ирвина и др. Выбор критерия зависит от вероятности принятия гипотезы нормального распределения и точности результатов обработки наблюдений (известны или нет генеральное среднее квадратическое отклонение и генеральное среднее).

НО если неизвестно генеральное СКО, то вычисляют выборочное среднее и выборочное СКО по форм. х=1/nΣx_{i ,} σ = √Σ(х_i-x)²/(n-1).

Чтобы принять решение об исключении или оставлении х_n в составе выборки находят отношение u_n=( х_n-x)/ σ. Результат сравнивают с критерием Романовского β. Если u_n≥ β, то сомнительный результат х_n исключают. Результат х₁ оценивают аналогично.

13. Виды измерений. Классификация измерений: прямые, косвенные, совместные, совокупные; равноточные и неравноточные, одно- и многократные, статические и динамические, методические и технические.

В зависимости от способов получения числовых значений измеряемых величин и их погрешностей все измерения делят на прямые, косвенные, совокупные и совместные. Целью такого деления является удобство при разработке методик выполнения измерений и обработки результатов.

Прямыми - измерения, при которых искомые значения величины находят непосредственно по показаниям средства измерений. Существенный признак: результат выражается непосредственно в тех же единицах, что и измеряемая величина. Скважинные измерения относят к прямым, если результат измерений получают непосредственно по шкале диаграммной ленты или по показаниям табло цифрового регистратора.

Косвенными - измерения, при которых значения величин находят по известной зависимости между измеряемой величиной и величинами, полученными в результате прямых измерений. В общем случае зависимость, связывающую измеряемую величину y и величины x₀, x_i, ..., x_n можно представить в виде явной функциональной зависимости. По виду функциональной зависимости различают косвенные измерения с линейной и нелинейной зависимостями. Вид связи между y и x определяет методику расчета погрешностей косвенных измерений.

Совокупными называют одновременно выполняемые измерения двух или нескольких одноименных величин, при которых значения искомых величин находят решением системы уравнений, получаемых при прямых измерениях. Например, определения значения уэс пласта по результатам измерений кажущихся значений уэс градиент зондами различного размера при условии, что диаметр скважины, уэс промывочной жидкости заранее известны.

Совместными называют одновременно выполняемые измерения двух или нескольких неодноименных величин для нахождения функциональной зависимости между ними. В практике геофизических исследований скважин применяются при градуировке СИ и для получения петрофизических связей. Например, совместными измерения являются измерения уэс горных пород, насыщающих их пластовых вод и коэффициентов пористости горных пород для нахождения зависимости относительного сопротивления от коэффициента пористости.

По точности измерения делятся на равноточные и неравноточные. Методика обработки результатов равноточных и неравноточных измерений различна.

В зависимости от числа измерений, проводимых во время эксперимента, различают одно- и многократные измерения. Известно, что при числе отдельных измерений более четырех их результаты могут быть обработаны в соответствии с требованиями математической статистики. Это означает, что при четырех и более измерениях, входящих в ряд, измерения можно считать многократными. Их проводят с целью уменьшения случайной составляющей погрешности.

В зависимости от влияния скорости изменения измерительной информации на результат измерения, в частности скорости движения скважинного прибора, измерения делятся на статические и динамические. Признаком, по которому измерение относят к статическому или динамическому, является динамическая погрешность при данной скорости или частоте изменения измеряемой величины и заданных динамических свойствах СИ. Если динамическая погрешность пренебрежимо мала для решаемой измерительной задачи, то измерение можно считать статическим (квазистатическим). При невыполнении указанных требований оно является динамическим.

По степени влияния условий измерений различают методические и технические измерения. При методических измерениях в обязательном порядке учитываются погрешности, а при технических – принимается погрешность, указанная в паспорте средства измерения или в нормативно-технической документации. Поэтому при технических измерениях нет необходимости определять и анализировать погрешности получаемых результатов.