Анализ чувствительности – это метод, точно показывающий, насколько изменяется npv и irr проекта в ответ на данное изменение одной входной переменной притом, что все остальные переменные не меняются.

Ключевые переменные в нашем случае – объем произведенной продукции, цена реализации, переменные затраты на единицу продукции и постоянные затраты.

Отклонение от базового уровня, %	NPV при изменении (млн.руб.)
	объема продукции	цены реализации	переменных затрат на ед.продукции	постоянных затрат
-10	119	119	161	166
-5	137	137	159	161
0	156	156	156	156
+5	174	175	154	151
+10	194	194	153	147

NPV проекта очень чувствителен к изменению объема продукции и цены реализации, довольно чувствителен к изменению постоянных затрат и относительно нечувствителен к изменению переменных затрат на единицу продукции.

Наклон линий показывает, насколько чувствителен NPV проекта к изменениям на каждом входе: чем круче наклон, тем чувствительнее NPV к изменению переменной.

4.2. Составить оптимальный инвестиционный портфель. Финансовые ресурсы –509.

а) проекты можно внедрять по частям

б) проекты нельзя внедрять по частям

Срок внедрения всех проектов 2 года.

Проект А, первоначальные инвестиции 200: Год 1 2 Доход 125 150 вероятность 0,9 0,9	Проект Б, первоначальные инвестиции 80: год 1 2 доход 85 100 вероятность 0,8 0,9
Проект В, первоначальные инвестиции 90: Год 1 2 Доход 104 145 вероятность 0,9 0,8	Проект Г, первоначальные инвестиции 150: год 1 2 доход 94 125 вероятность 0,9 0,9
Проект Д, первоначальные инвестиции 100: Год 1 2 Доход 74 95 вероятность 0,9 0,9

Решение:

Для расчета показателей эффективности необходимо использовать следующие формулы:

,

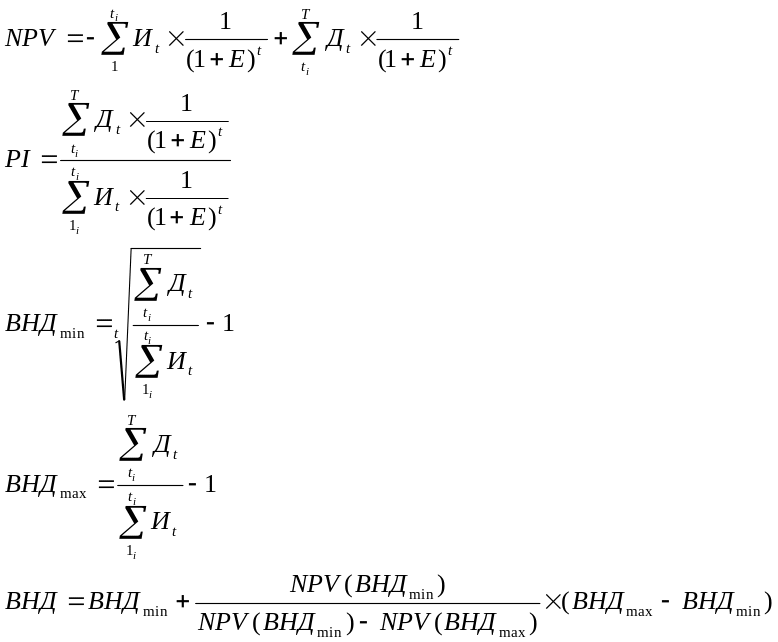где - денежные потоки по шагам расчетного периода;

- инвестиции по шагам расчетного периода;

- норма (ставка) дисконта (норма доходности инвестиций);

- горизонт расчета (число лет жизненного цикла проекта).

Проект	Инвестиции, д. е.	Доходы по годам, д. е.
		1 год	2 год	3 год
А	-200	80	100	180
Б	-240	100	180	140
В	-220	140	140	100

Подставляя исходные данные в вышеуказанные формулы, рассчитаем чистый дисконтированный доход NPV, индекс доходности PI и внутреннюю норму доходности ВНД по всем трем проектам. Далее необходимо проранжировать по индексу доходности PI в порядке убывания его значения. В результате получим следующие показатели:

Проект	NPV, д. е.	PI	ВНД,%
А	91	1,455	31,0
В	98	1,445	35,7
Б	105	1,438	32,0

Далее если для проектов допустимо их дробление, то решение задачи будет выглядеть следующим образом. Сумма инвестиций по первым двум проектам составляет 420 д. е., что меньше исходного ограничения инвестиций в 500 д. е. Следовательно, проект В может быть реализован в планом году на сумму в 80 д. е., что в процентном выражении составляет 33,33%. Таким образом оптимальный портфель для предприятия в этом случае будет включать проекты А и В, реализованных на 100%, и проект В, осуществленный на 33,33%.

Проект	Объем инвестиций, д. е.	Часть инвестиций, включаемая в инвестиционный портфель,%	NPV, д. е.
А	-200	100	91
В	-220	100	98
	-420<500		189
Б	500-420=80	80/240*100=33,3	105*33,3=35
	500		224

4.3. Составить оптимальный инвестиционный портфель на 3 года стоимостью 295 д.е. каждый год.

а) проекты можно внедрять по частям

б) проекты нельзя внедрять по частям

Срок внедрения всех проектов 2 года.

Проект А, первоначальные инвестиции 50: Год 1 2 Доход 34 50 вероятность 0,9 0,9	Проект Б, первоначальные инвестиции 80: год 1 2 доход 80 95 вероятность 0,9 0,9
Проект В, первоначальные инвестиции 90: Год 1 2 Доход 95 150 вероятность 0,9 0,9	Проект Г, первоначальные инвестиции 150: год 1 2 доход 100 126 вероятность 0,9 0,9
Проект Д, первоначальные инвестиции 100: Год 1 2 Доход 74 100 вероятность 0,9 0,9

Решение:

В случае, если проекты не могут быть перенесены на другой период времени, то суть решения задачи об отборе наиболее эффективных проектов сводится к простому сложению показателей NPV по проектам. При этом необходимо помнить об существующем финансовом ограничении в 500 д. е.

Вариант	Общий объем инвестиций, д. е.	Суммарный NPV, д. е.
А+Б+В	200+240+220=660>500	Сочетание невозможно
А+Б	200+240=440<500	91+105=196
А+В	200+220=420<500	91+98=187
Б+В	240+220=460<500	105+98=203

Таким образом, в дном случае более всего целесообразно инвестировать в проекты Б и В с целью достижения максимально эффективности.

По тем же исходным параметрам необходимо составить оптимальный инвестиционный портфель предприятия на 2 года, если объем инвестиций ограничен суммой 400 д. е.; Е=10%.

Для решения этой задачи необходимо, используя нижеприведенные формулы, рассчитать потери чистого дисконтированного дохода и индекс возможных потерь, если реализация каждого инвестиционного проекта будет отложена на 1 год.

,

Проект	И, д. е.	NPVn, д. е.		NPVc, д. е.	Потери NPV, д. е.	Индекс возможных потерь (I)
А	-200	91	0,909	82,7	8,3	0,0415
Б	-240	105	0,909	95,5	9,5	0,0396
В	-220	98	0,909	89,1	8,9	0,0404

Из вышеприведенной таблицы видно, что наименьшие потери будут, если предприятие отложит на 1 год реализацию проекта Б ( ), затем проектов В и А. Далее, аналогично примеру 1, необходимо сформировать итоговый инвестиционный портфель на 2 года.

Проект	Объем инвестиций, д. е.	Часть инвестиций, включаемая в портфель,%	NPV, д. е.
Первый год
А	-200	100	91
В	400-200=-200	200/220*100=90,9	98*0,909=89,1
	-400		180,1
Второй год
В	-20	20/220*100=9,1	89,1*0,091=8,1
Б	-240	100	95,5
	-260		103,6

Суммарный NPV за 2 года: 180,1+103,6=283,7 д. е.

Общие потери от переноса реализации части инвестиционных проектов на 1 год составят: (91+105+98) - 283,7=10,3 д. е. и будут минимальными по сравнению с другими вариантами формирования портфелей.