35

КОНТРОЛЬНАЯ РАБОТА №1

Финансовая математика

Вариант № 45(М=4,N =5)

Содержание

Тема 1. Расчеты с простыми и сложными процентными ставками 3

Тема 2. Количественный анализ потоков платежей 12

Тема 3. Планирование погашения долгосрочных задолженностей (кредитов) 15

Тема 4. Анализ эффективности инвестиций 20

Анализ чувствительности – это метод, точно показывающий, насколько изменяется NPV и IRR проекта в ответ на данное изменение одной входной переменной притом, что все остальные переменные не меняются. 22

Тема 5. Анализ эффективности операций с ценными бумагами 28

Список литературы 35

Тема 1. Расчеты с простыми и сложными процентными ставками

1. Ссуда в размере 100050 руб. выдана 24 января под 6% годовых. Срок возврата ссуды 15 сентября. Определить размер погасительного платежа, применяя:

а) точные проценты с фактическим числом дней ссуды;

б) обыкновенные проценты с фактическим числом дней ссуды;

г) обыкновенные проценты с приближенным числом дней ссуды.

Решение:

а) К = 365, t = 73, I = 100050 х 0,6 х 73 / 365 = 10 000,00 руб.

б) К = 360, t = 73, I = 100050 х 0,6 х 73 / 360 = 17 638,89 руб.

в) К = 360, t = 74, I = 100050 х 0,6 х 74 / 360 = 15 277,78 руб.

2. Контракт предусматривает следующий порядок начисления процентов: первый год – 5%, а в каждом следующем квартале ставка повышается на 0,5%. Определить множитель наращения за два года.

Решение:

Множитель наращения за два года = 5 + 5 * 0,5 + 0,5 * 0,55 + 0,5 * 0,6 = 1,215.

3. Вексель на сумму 500 000 руб. учли в банке за 200 дней до погашения по учетной ставке 7%, (К=360). Определите

а) полученную при учете сумму и дисконт;

б) процентную ставку в случае применения математического дисконтирования с тем же дисконтом.

Решение:

В случае простого дисконта:

P = S (1 - nd);

Выручка:

P = 500000 (1 – 0,07* 72/365) = 399300 руб.

Дисконт составит:

500000 – 399300 = 100700 руб.

3. Владельцу векселя на 10 000 руб. с датой погашения 6 августа требуется сумма 1036 руб. Раньше какой даты он не сможет получить требуемую сумму, если простая учетная ставка в банке равна 10%.

Решение:

Найдем сумму дисконта:

10000-Х=1036 руб.

Х=8964 руб.

Найдем количество дней между датой учета и датой погашения, воспользовавшись формулой:

I-Kn*d/D,

где

I - дисконт

K_n – номинальная величина векселя;

d – число дней от момента дисконтирования до даты погашения векселя;

D – процентный ключ или дивизор (D = 360*100/p = 36000/10 = 3600).

10000*d/3600=8964

d=3240

3. Определите сумму консолидированного на 1 августа платежа, если при начислении процентов по ставке 10% использовался метод 365/360. Консолидируются платежи: 20 000 руб., 50 000 руб. и 30 000 руб. со сроками 19 мая, 20 июня и 26 августа.

Решение:

Определим временной интервал между сроками для первого платежа и консолидированного платежа (дата выдачи и дата погашения считается за один день):

t₁= 11(май) + 31(июнь) - 1= 41 день;

для второго платежа и консолидированного платежа:

t² = 22(май) - 1 = 21 день.

Отсюда сумма консолидированного платежа будет равна:

FV_oб. = FV₁ * (1 + t₁/T * i) + FV₂ * (1 + t₂/T * i) =

= 20'000 * (1 + 41/360 * 0,1) + 30'000 * (1 + 21/360 * 0,1) = 50'402,78 руб.

Таким образом, консолидированный платеж со сроком 01.08. составит 50'402,78 руб.

3. Кредит в размере 11 тыс. руб. выдан на 2 года 150 дней. Контрактом предусмотрена ставка сложных процентов, равная 8% годовых.

Определите сумму долга на конец срока, используя:

а) точный метод начисления сложных процентов;

б) смешанный метод начисления сложных процентов.

Решение:

Если начисляются точные проценты, то

S=200*(1+31/365*0,12)*(1+28/365*0,12)*(1+31/365*0,12)=205,97 руб.

Начисление обыкновенных процентов (германская практика) дает значение наращенной суммы

S=200*(1+30/360*0,12)³=206,06 руб.

3. Кредит выдается на полтора года по сложной годовой учетной ставке 16%. Какова сумма долга и величина дисконта, если выданная сумма равна 6 тыс. руб.?

Решение:

Эквивалентная процентная ставка:

j = (1+ i)^m/n -1 =(1+ 0,05)^10/3 -1;

(1+ i)^m = (1+ j)ⁿ = (1 + 0,05)¹⁰

(1+ j)ⁿ = (1 + 0,05)¹⁰ = 1,6289

отсюда:

(1+ i)³ =1,6289; (1+ i) = 1,1768; i = 0,1768 ≈ 17,7%

По ставке сложного процента:

при n = 3 и 5 %

Будущая стоимость единицы: 1,1576

S_n = P(1+i)ⁿ

Р = 10000/1,6289 = 6139,11 руб.

тогда: 6139,11*1,1576 = 7139,63 руб.

3. Номинальная процентная ставка 14% годовых. Какова эффективная процентная ставка, если проценты начисляются:

а) по полугодиям,

б) ежеквартально,

в) ежемесячно?

Решение:

Эффективная процентная ставка:

при n=1 год: ;

3. Сравните условия вложения средств в банк в следующих случаях:

а) номинальная ставка 14% при ежемесячном начислении процентов;

б) номинальная ставка 15% при ежеквартальном начислении процентов;

в) номинальная ставка 16% при начислении процентов каждые полгода.

Сравнение проведите двумя способами:

1) используя эффективную ставку;

2) рассчитывая время удвоения.

Решение:

Решение: n = 1 год

1) m = 12, j =14% = 0,14

2) m = 4, j =15% = 0,15

3) m = 2, j = 16% = 0,16

Эффективная процентная ставка:

при n=1 год: ;

Ответ: выдача кредитов под 16% годовых с полугодовым начислением процентов банку выгоднее, т.к. эффективная годовая процентная ставка в этом случае больше (сумма кредита возрастает на 17,7% за год).

3. Кредит в сумме 29 тыс. руб. взят на 5 лет с ежегодным начислением процентов по ставке 6%. Соглашение пересмотрено так, что через 3 года производится выплата 10 тыс. руб., а еще через 3 года выплачивается оставшаяся часть долга.

Определите сумму окончательного платежа.

Решение:

i = 6% = 0,06

n = 5 лет

FVA = 29 000 руб.

Размер ежегодных платежей:

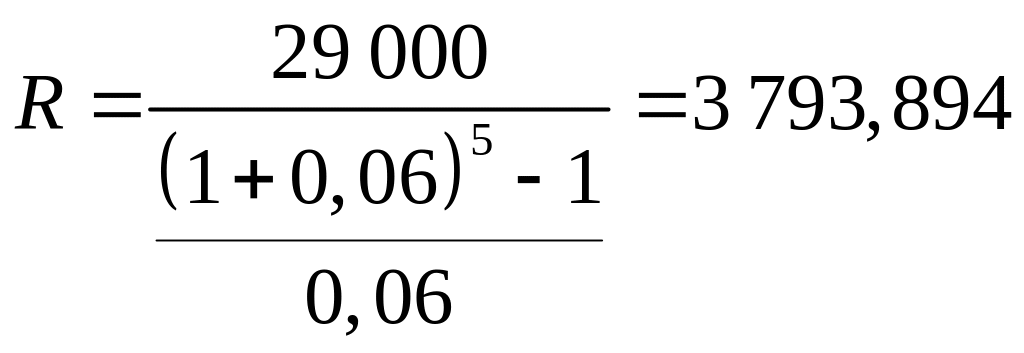руб.

3. На сумму 1,5 млн руб. в течение трех месяцев начисляются простые проценты из расчета 27,5% годовых. Ежемесячная инфляция в рассматриваемом периоде характеризуется темпами 2,5; 2 и 1,8%. Определить наращенную сумму с учетом инфляции.

Решение:

Наращенная сумма = 1,5*(1+(90,275/12)*3))

Индекс цен равен 1,025 х 1,02 х 1,018 = 1,06432.

С учетом обесценивания наращенная сумма составит

 1,605 - 1,06432  = 1,508 млн. руб. 

Ответ: 1,508 млн. руб.

3. По срочному годовому рублевому вкладу платят 41% годовых. Прогноз повышения курса доллара за год – с 25 руб. до 35 руб. Какое принимать решение: нести рубли в банк или купить на них доллары и хранить их в «в банке в тумбочке»?

Решение:

Во втором случае рублевый вклад увеличится в 35/25=1,4 раза, т.е. на 40%.

Следовательно, выгоднее положить в банк (41%>40%).

3. Какая должна быть ставка сложных процентов, чтобы при инфляции 4% в полгода обеспечивалось реальное наращивание денежных средств в размере 9% годовых?

Решение:

S_n = P(1+i)ⁿ

2 = 1 (1+i)¹²

(1+i)¹² =2

Прологарифмируем полученное выражение:

12 lg (1+i) = lg2; lg2 = 0,3

12 lg (1+i) = 0,3

lg (1+i) = 0,0025; (1+i) = 1, 06; i = 0,06 (6%)

3. Определить реальную годовую ставку доходности, если номинальная ставка 20%, а квартальный темп инфляции составляет 2%.

Решение:

Решение: n = 1 год i = 20% = 0,2 = 2% = 0,02 N = 4

Индекс цен:

Реальная годовая процентная ставка:

Ответ: реальная годовая ставка процентов равна 16,9%.

3. В 1993 году в России можно было поместить деньги под 504% годовых. Инфляция в этом году составляла примерно 906%. Какова доходность вложения?

Решение:

Допустим, 100 вложено

+ 504 = 604 получили 

100 + 906 = 1006 

То есть инфляция обесценила всё в 10 раз  604 / 10 = 6,04.

С вложенных 100 получили 60,4 доходность - 39,6%.