
- •12. Ангармоникалық тербелістер.
- •14. Бұрыштық жылдамдық. Бұрыштық жылдамдықтың қозғалыстағы санақ жүйесінің остеріне проекциялары. Лездік айналу осі.
- •15. Абсолютті қатты дененің инерция тензоры. Инерцияның бас остері.
- •16. Инерция моменттері бас остері. Ассимметриялы ұршық.
- •17. Инерция моменттері бас остері. Симметриялы ұршық.
- •18. Инерция моменттері бас остері. Сызықтық ұршық.
- •19. Қатты дененің импульс моменті.
- •20. Қатты дененің қозғалыс теңдеулері.
- •21. Күш моменті.
- •22. Бір нүктесі бекітілген абсолют қатты дене үшін Эйлердің қозғалыс теңдеулері.
- •27. Якоби теңдігі.
- •28. Гамильтон-Якоби теңдеуі.
- •29. Гамильтон-Якоби теңдеуінің математикалық құрылысы. Толық интегралы.
- •30. Айнымалыларды ажырату тәсілі.
19. Қатты дененің импульс моменті.
Қатты дененің еркіндік дәрежесі алтыға тең болғандықтан, қозғалыс теңдеулер жүйесі алты тәуелсіз теңдеулерден тұруы керек. Оларды дененің импульс және момент векторларының уақыт бойынша туындысы ретінде жазуға болады.
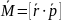 – импульс
моменті
– импульс
моменті
 ,
,
 – қатты дененің импульс моменті,
– қатты дененің импульс моменті,
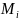 – импулсь
моментінің тензоры.
– импулсь
моментінің тензоры.




 – тензорлық
түрде.
– тензорлық
түрде.
20. Қатты дененің қозғалыс теңдеулері.
 ,
,
 (1)
(1)
 (2),
(2),
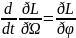 (3)
(3)
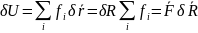

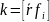
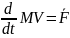 (4),
(4),
 (5),
(5),
 ,
,

21. Күш моменті.
қозғалыс
теңдеулерін импульс моментінің
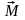 уақыт бойынша туындысы ретінде алайық.
уақыт бойынша туындысы ретінде алайық.
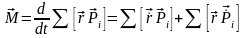 . (1)
. (1)
Таңдап
алған санақ жүйесінде
 ,
,
 болады.
және
болады.
және
 векторлары бағыттас болғандықтан
векторлары бағыттас болғандықтан
 (2)
(2)
 (3)
(3)
болғандықтан
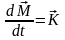 . (4)
. (4)
Себебі  (5)
(5)
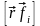 – векторы
– векторы
 күшінің
моменті деп
аталады. Сондықтан
күшінің
моменті деп
аталады. Сондықтан
 – денеге әсер ететін барлық күштердің
моменттерінің қосындысына тең болып
табылады.
– денеге әсер ететін барлық күштердің
моменттерінің қосындысына тең болып
табылады.
Егер
координаттар басын
қашықтығында алатын болсақ нүктелердің
жаңа радиус векторлары –
 ,
ескі радиус-вектор
арасындағы байланыс:
,
ескі радиус-вектор
арасындағы байланыс:
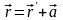 (6)
(6)
болса
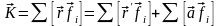 (7)
(7)
немесе
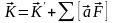 (8)
(8)
Осыдан
көріп тұрғанымыздай егер
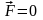 болса, күш моменті координаттардың
бастапқы орнына тәуелді емес.
болса, күш моменті координаттардың
бастапқы орнына тәуелді емес.
Егер
 және
векторлары өзара перпендикуляр болса
(8) формуладағы
және
векторлары өзара перпендикуляр болса
(8) формуладағы
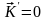 айналатын кез-келген
векторын таңдап алуға болатындықтан:
айналатын кез-келген
векторын таңдап алуға болатындықтан:
 . (9)
. (9)
Сонымен, қатты дененің біртекті өрісте қозғалысы кезінде өрістің әсері радиус векторы нүктеге берілген бір ғана күшімен сипатталады.
22. Бір нүктесі бекітілген абсолют қатты дене үшін Эйлердің қозғалыс теңдеулері.
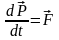
(1)
қозғалыс
теңдеулерін x,y,z
қозғалыстағы координаттар үшін жазайық.
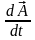 – кез-келген бір
– кез-келген бір
 векторының тыныштықтағы координаттар
жүйесіне қатысты алғандағы уақыт бойынша
өзгерісі деп алайық.
векторының тыныштықтағы координаттар
жүйесіне қатысты алғандағы уақыт бойынша
өзгерісі деп алайық.
 (2)
(2)
 . (3)
. (3)
Осы жалпы формуланы пайдаланып (1) өрнекті қайта жазамыз:
 (4)
(4)
 (5)
(5)
Уақыт бойынша дифференциалдау қозғалыстағы санақ жүйесінде жүргізілгендіктен, теңдеулерді осы осьтердегі проекциялары арқылы жаза аламыз:
 (6)
(6)
 (7)
(7)
Мұндағы
1,2,3 индекстері x`,y`,z` осьтеріндегі осы
теңдеулердің құраушыларын білдіреді.
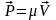 алмастырып:
алмастырып:
 ,
,
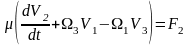 ,
,
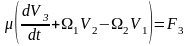 . (8)
. (8)
x`,y`,z`
осьтері инерциясының бас осьтері арқылы
өтеді дей отыра, (5) теңдеуін
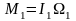 ,
,
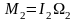 ,
,
 өрнектерін пайдаланып жазамыз:
өрнектерін пайдаланып жазамыз:
 ,
,
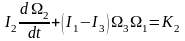 ,
,
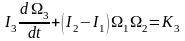 .
(9)
.
(9)
Осы теңдеулер Эйлер теңдеулері деп аталады.
23. Инерциалды емес санақ жүйелеріндегі қозғалыс.
 (1),
(1),
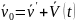 (2),
(2),

 (3)
(инерциалды
емес санақ жүйесінде Лагранж функциясы)
(3)
(инерциалды
емес санақ жүйесінде Лагранж функциясы)
Лагранж
теңдеуі,
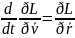 (4),
(4),
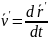 (5)
(5)
 (6)
(6)
 (7)
үдеу
(7)
үдеу
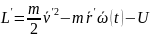 (8),
(8),
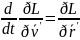 (9),
(9),
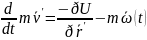 (10),
(10),
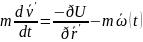 (11)
қозғалыс теңдеуі.
(11)
қозғалыс теңдеуі.
24. Инерциалды емес санақ жүйелеріндегі денелердің айналмалы қозғалыс теңдеуі.
,
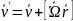 (1),
(1),
(2),
 (3)
(3)
 (4)
(4)
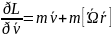 (5),
(5),
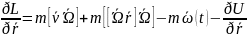 (6)
(6)
 (7)
(7)
 – кориолис
күші,
– кориолис
күші,
 – центрден тепкіш күш.
– центрден тепкіш күш.
25. Инерциалды емес санақ жүйелеріндегі толық энергия.
 (үдеу),
(үдеу),
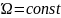 (бұрыштық
жылдамдық)
(бұрыштық
жылдамдық)
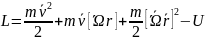 (1)
(1)
 ,
,
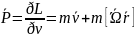 ,
,
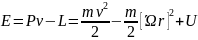 ,
,
Центрден тепкіш потенциалдық энергия.
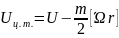 .
.
26. Пуассон жақшалары. Пуассон жақшаларының қасиеттері.
 функциясын
– координата, импулсь және уақыттың
функциясы ретінде қарастыралық. Оның
уақыт бойынша толық туындысын қарастыратын
болсақ
функциясын
– координата, импулсь және уақыттың
функциясы ретінде қарастыралық. Оның
уақыт бойынша толық туындысын қарастыратын
болсақ
 (1)
(1)
Гамильтон теңдеулерін қолданамыз
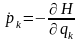 ;
;
 . (2)
. (2)
(1)-ге қойғанда
 (3)
(3)
Мынадай белгілеу енгізсек
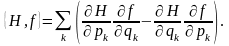 (4)
(4)
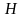 және
және
 -ке
арналған өрнекті Пуассон
жақшалары
деп атайды.
-ке
арналған өрнекті Пуассон
жақшалары
деп атайды.
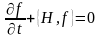 (5)
(5)
Егер де қозғалыс интегралы анық уақыттан тәуелсіз болса
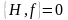 , (6)
, (6)
яғни, оның Гамильтон функциясымен
алынған
Пуассон жақшасы нөлге айналуы тиіс.
Кез-келген
және
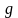 шамаларының құраған Пуассон жақшалары
да осындай жолмен табылады
шамаларының құраған Пуассон жақшалары
да осындай жолмен табылады
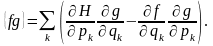 (7)
(7)
Пуассон жақшаларының қасиеттері:
Егер де функциялардың орнын алмастырса, жақшаның таңбасы өзгереді:
 (8)
(8)
Егер функциялардың бірі тұрақты шама болса, жақша нөлге айналады:
 . (9)
. (9)
