3 Этап:
;
;
;
Зная,
что
,
подставим
и получим
;
;
;
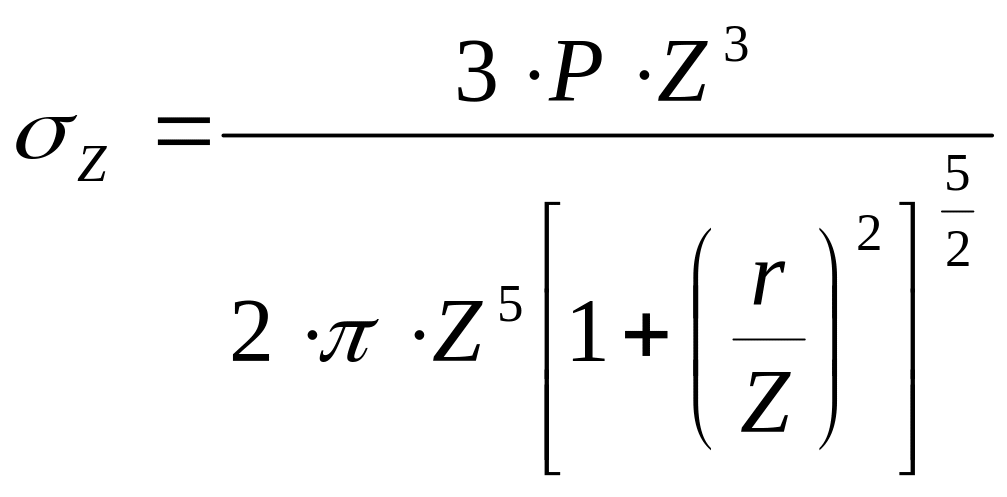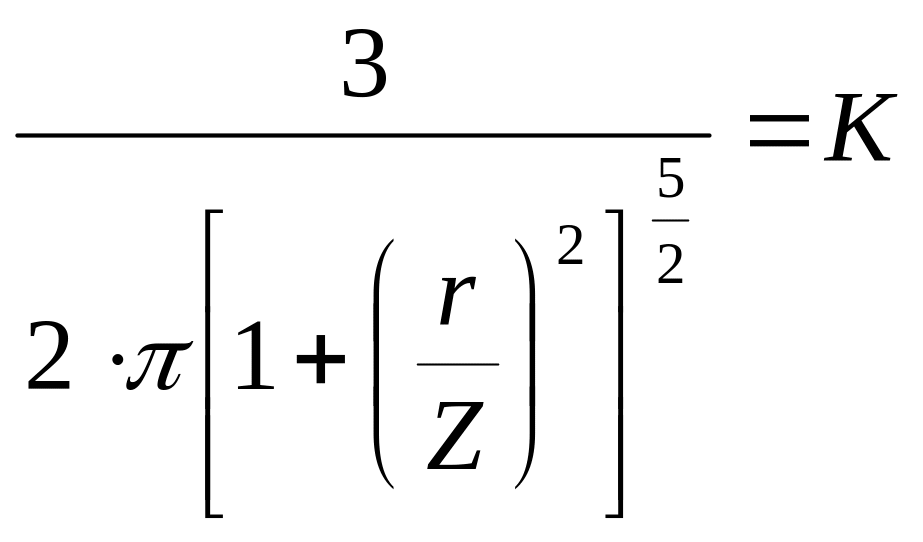- опред. по
таблице
;
5.4 Определение напряжений в массиве грунта от действия нескольких сосредоточенных сил.
(принцип Сен-Венана – принцип независимости действия сил)
Р1 Р2 Р3
Z r2
r
|
|
3
K=f
5.4 Определение напряжений при действии любой распределённой нагрузки (метод элементарного суммирования)
Z R
элемент
|
Задачу решаем приближённо. Разбиваем площадь на ряд простых многоугольников.Рассмотрим ri элемент
zi=Ki Pi – нагрузка на данный элемент
zi
= |
Pi
Pi=qifi
M
r
М r
Ki=f ; Эта задача трудоёмкая, особенно при большом числе элементов
1- способ универсален |
Недостатки:
2- значительная трудоемкость |
Достоинства:5.5 Определение – под центром прямоугольной площадки загружения при равномерной нагрузке
в
Z
|
– можно определить в интегральной форме
=
- в табл. СНиП, справочниках, учебниках. |
Р
Z
M
L
- при
разворачивании этого интеграла
получается очень громоздкая формула,
поэтому её приводят к элементарному
(простейшему) виду:
;
где
= f
5.6 Определение напряжений – по методу угловых точек
(в любой точке под нагрузкой и на любой глубине)
|
Достраиваем площадь так, чтобы точка М была в центре, тогда видно, что
=
а не 2Z, т.к. в1=2в Разбив площадь подобным образом, можно записать
= Р – интенсивность давления
|
,
но
,
1
|
Так мы сможем решить любую задачу по опред. – на любом расстоянии и на любой глубине. Данный способ находит приминение При учете взаимного влияния фундаментов. |
=
