3.4. Графики:
а) точное и приближенное решения
б) погрешности приближения
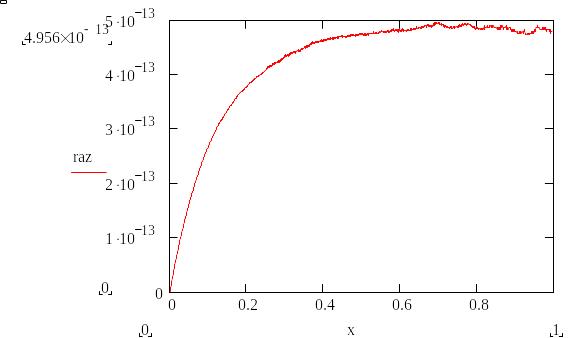
3.5. Вывод.
Для заданной задачи Коши получено аналитическое решение и
численное решение методом Рунге-Кутта (функция rkfixed).
Погрешность выбранного численного метода решения для данной
задачи Коши не превышает 5·10^–13.
Метод Рунге-Кутта позволяет получить численное решение (в табличном виде) таких дифференциальных уравнений. Подбор шага метода позволяет численно строить приближённые решения практически с любой заданной точностью.
Список использованных источников
1. Румянцев С.А. Основы математического моделирования и
вычислительной математики. Екатеринбург, УрГУПС, 2006.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление для
вузов.Т. 1,2.
3. Куликова О.В., Поповский Э.Е., Скачков П.П. Применение системы
MathCad для исследования функции одной переменной. Методические
рекомендации. Екатеринбург, УрГУПС, 2005. 66 с.
4. Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. для вузов.
М.: Высш.шк., 1998.
5. Советов Б.Я., Яковлев С.А. Моделирование систем. Практикум:
Учеб. пособие для вузов. М.: Высш.шк., 1999.
6. Белугин В.И. и др. Математическая обработка результатов
эксперимента. Екатеринбург: УРГУПС, 1998, 64 с.
7. Тимофеева Г.А. Экономико-математические модели управления.
Екатеринбург: УРГУПС, 2000, 48 с.