Содержание
Введение…………………………………………………….……………………..3
1 Проецирование заданной функции на отрезок ряда Фурье…….……………4
Постановка задачи……………………………………………………………4
Метод решения………………………………………………………………..4
Текст программы на MathCAD с комментариями к операторам………….5
Графики:
а) исходная и приближающие зависимости………………...………………6
б) погрешности приближения………………………………………………..7
1.5 Выводы………………………………………………………………………...8
2 Приближение по методу наименьших квадратов табличных данных двумя конкретными системами базисных функций……………………………….…..9
2.1 Постановка задачи………………………………………………………....…9
2.2 Метод решения………………………………………………………….…....9
Текст программы на MathCad с комментариями к операторам……….…10
Графики:
а) исходная и приближающие зависимости……………………………….12
б) погрешности приближений: среднеквадратическая и поточечная…………………………………………………………………...14
2.5 Выводы…………………………………………………………………….…15
3 Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка……………………………………………………..16
3.1 Постановка задачи………………………………………………………...…16
Метод решения……………………………………………………………….16
Текст программы на MathCad с комментариями к операторам………..…18
3.4 Графики:
а) точное и приближенное решение………………………………………..18
б) погрешности приближения……………………………………………....19
3.5 Выводы…………………………………………………………………….…19
Список использованных источников………………………….………………..20
Введение
Методы математического моделирования играют важную роль в
инженерных расчетах и проектировании сложных электротехнических систем.
Моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим близкое к оригиналу поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала путем исследования его модели, а не самого объекта. Разумеется, моделирование оправдано в том случае когда оно проще создания самого оригинала или когда последний по каким-то причинам лучше вообще не создавать.
С помощью интегрированной системы программирования ориентированной на проведение математических и инженерно-технических расчетов MathCAD будут рассмотрены следующие практические задачи и найдены пути их решения:
1 Проецирование заданной функции на отрезок ряда Фурье,
2 Приближение по методу наименьших квадратов табличных данных двумя конкретными системами базисных функций,
3 Численное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
Для каждой практического задания будет сформулирована задача, оговорен метод решения, представлен текст программы на MathCAD с комментариями к операторам, представлены графики полученных исследований и сформулирован вывод по полученному исследованию.
1 Проецирование заданной функции на отрезок ряда Фурье.
Постановка задачи.
С помощью вычисления определенных интегралов спроецировать заданную на отрезке [0;2] функцию на отрезок ряда Фурье решить отрезками тригонометрических рядов только по синусам или только по косинусам.
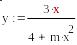при
m:=2
Метод Решения:
По косинусу:
1.Вычислим определенный интеграл для заданной функции на отрезке [0;2];
2. Вычислим определенный интеграл для заданной функции на отрезке [0;2] отрезками тригонометрических рядов по косинусу для n элементов;
3. Спроецируем заданную функцию на отрезок ряда Фурье по формуле
;
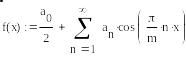где
,
4. Построим график зависимости заданной функции и отрезка ряда Фурье по косинусу;
5. Построим график разности отрезка ряда Фурье и заданной функции;
По синусу:
1.Вычислим определенный интеграл для заданной функции на отрезке [0;2];
2. Вычислим определенный интеграл для заданной функции на отрезке [0;2] отрезками тригонометрических рядов по синусу для n элементов;
3. Спроецируем заданную функцию на отрезок ряда Фурье по формуле
;
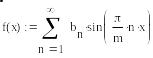где
4. Построим график зависимости заданной функции и отрезка ряда Фурье по синусу;
5. Построим график разности отрезка ряда Фурье и заданной функции;
Текст программы на MathCad с комментариями к операторам
По косинусу:
По синусу:
Графики:
а) Исходная и приближающие зависимости:
По косинусу:
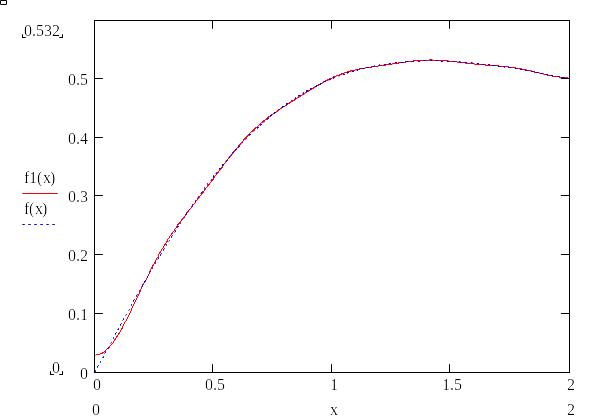
По синусу:
б) Погрешности приближения
По косинусу:
По синусу:
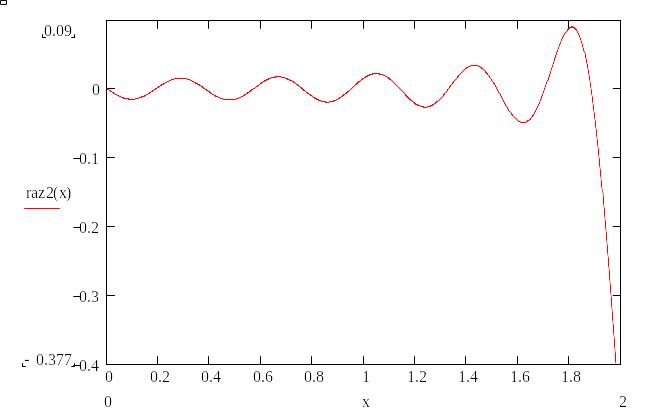
1.5 Вывод:
С помощью вычислений определенных интегралов была спроецирована заданная функция на отрезок ряда Фурье путем тригонометрических рядов по формуле синусов и косинусов в пределах [0;2].
По результатам построения графиков спроецированной функций и графиков погрешности выяснилось, что погрешность функции при использование метода по косинуса находится в пределах [-0,01;0,03].
Погрешность функции при использование метода по синусу находится в пределах [-0,4;0,09].
Следовательно метод косинусов для данной данной функции является более точным в сравнение с методом по синусу.
2 Приближение по методу наименьших квадратов табличных данных двумя конкретными системами базисных функций.
2.1. Программой linfit требуется приблизить таблично заданную
функцию на отрезке от [0;2] с заданным числом точек М=200 по методу
наименьших квадратов для указанной системы базисных функций
, где
m=2
2.2. Метод решения.
Метод наименьших квадратов применяется для нахождения оценок параметров функциональной зависимости между переменными, значения которых определяются из опыта.
Для базисной функции по косинусу:
1 Вычислим коэффициенты линейной базисной функции F(x)
по методу наименьших квадратов с помощью программы linfit (x,y,F);
2 Приблизим табличные данные базисной функции ;
3 Рассчитаем погрешность точного решения;
4 Рассчитаем среднеквадратичную погрешность;
5 Построим график исходной зависимости функции
, где m=2;
6 Построим график приближающей зависимости;
7 Построим график поточечной погрешности.
Для базисной функции по синусу:
1 Вычислим коэффициенты линейной базисной функции F(x)
по методу наименьших квадратов с помощью программы linfit (x,y,F);
2 Приблизим табличные данные базисной функции ;
3 Рассчитаем погрешность точного решения;
4 Рассчитаем среднеквадратичную погрешность;
5 Построим график исходной зависимости функции
, где m=2;
6 Построим график приближающей зависимости;
7 Построим график поточечной погрешности.