2.3. Расчет статически неопределимых систем смешанным методом

В смешанном методе неизвестными параметрами являются силы и перемещения. Основная система (ОС) смешанного метода получается из заданной системы путем отбрасывания связей в одной ее части и введения дополнительных связей в другой части. Отброшенные связи заменяются неизвестными силами , в направлениях дополнительных связей указываются неизвестные перемещения . Канонические уравнения смешанного метода строятся исходя из их физического смысла: отсутствия перемещений в ОС в направлениях неизвестных сил и отсутствия реакций дополнительных связей в направлениях неизвестных перемещений .

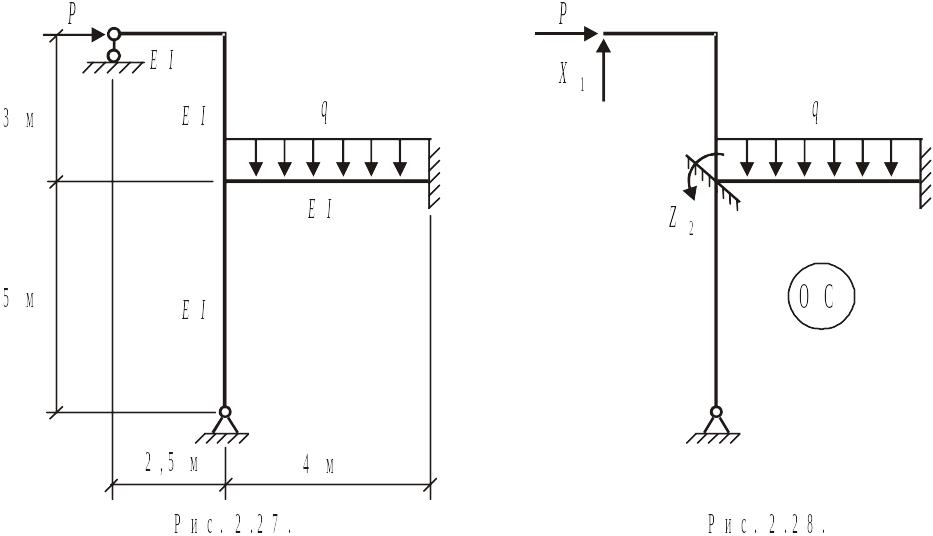
Пример расчета статически неопределимой

рамы (рис.2.27) смешанным методом.

Дано: . Построить эпюры .

1. Выбор ос

Минимальное количество неизвестных параметров (сил и перемещений) при выборе ОС получается путем отбрасывания опорного стержня и замены его неизвестной силой , и введения дополнительной связи (заделки), по направлению которой определяется обобщенное перемещение (угол поворота узла) (рис. 2.28). Неизвестные и определяются из канонических уравнений

Штрихами в канонических уравнениях обозначены смешанные коэффициенты, связанные между собою равенством и определяемые, исходя из их физического смысла: - перемещение в ОС в направлении силы от перемещения ; - реакция дополнительной связи в ОС в направлении перемещения от силы . Остальные коэффициенты и свободные члены уравнений имеют тот же смысл, что в методе сил (первое уравнение) и в методе перемещений (второе уравнение).

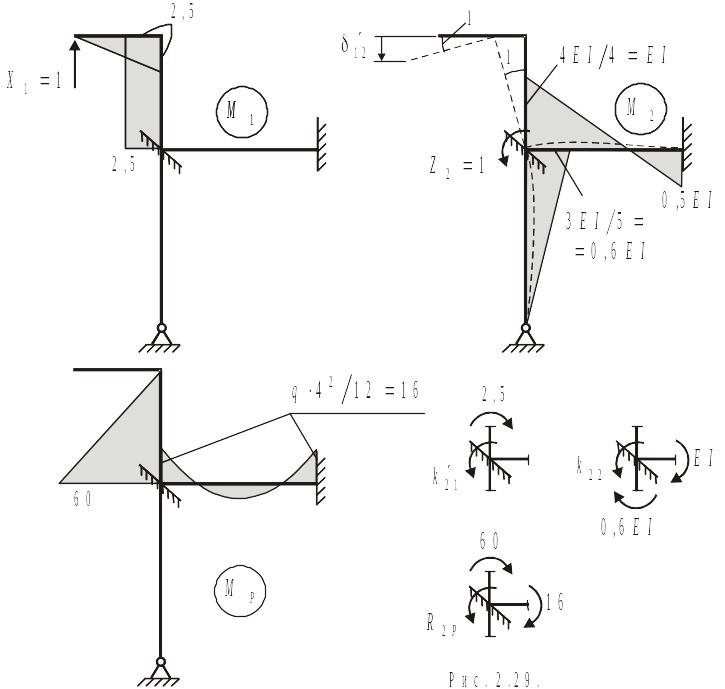
2. Построение эпюр в ос

Эпюры (рис. 2.29) строятся в ОС соответственно от силы , перемещения и нагрузки. Последние две эпюры строятся по справочным данным для типовых элементов метода перемещений (табл. 2.1).

3. Определение коэффициентов при неизвестных и свободных

членов канонических уравнений

Значения определяются по формуле Мора. Интегралы Мора на каждом участке находятся по справочным формулам перемножения эпюр или по правилу Верещагина.

Коэффициент находится из геометрических соображений (см. эпюру ): . Значения находятся из равновесия внешних и внутренних моментов в узле, содержащем дополнительную связь (рис.2.29): .

Подставляя найденные значения в канонические уравнения и решая последние, получаем: .

4. Построение эпюр в заданной системе

Эпюра (рис. 2.30) строится по принципу суперпозиции: (эпюры строятся отдельно).

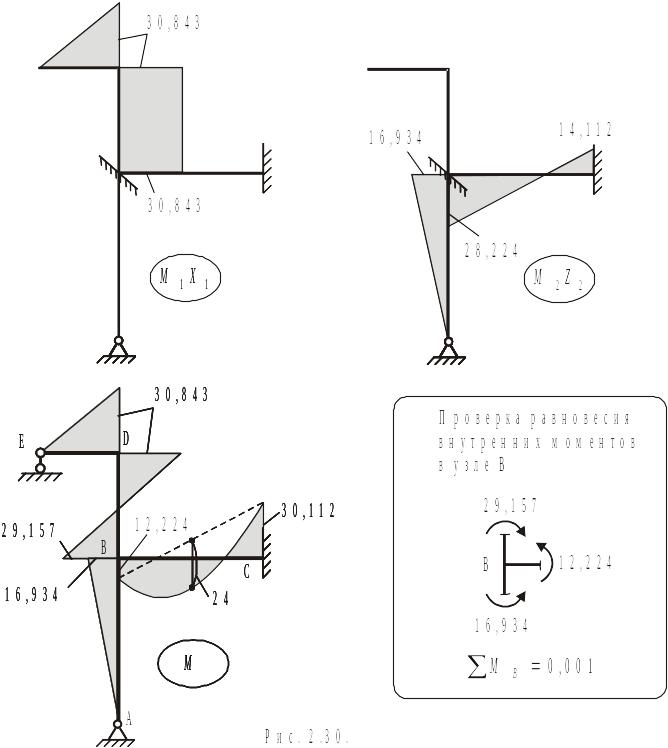
Находим поперечные силы на участках конструкции.

Участок AB:

Участок BD:

Участок ED:

Участок BC:

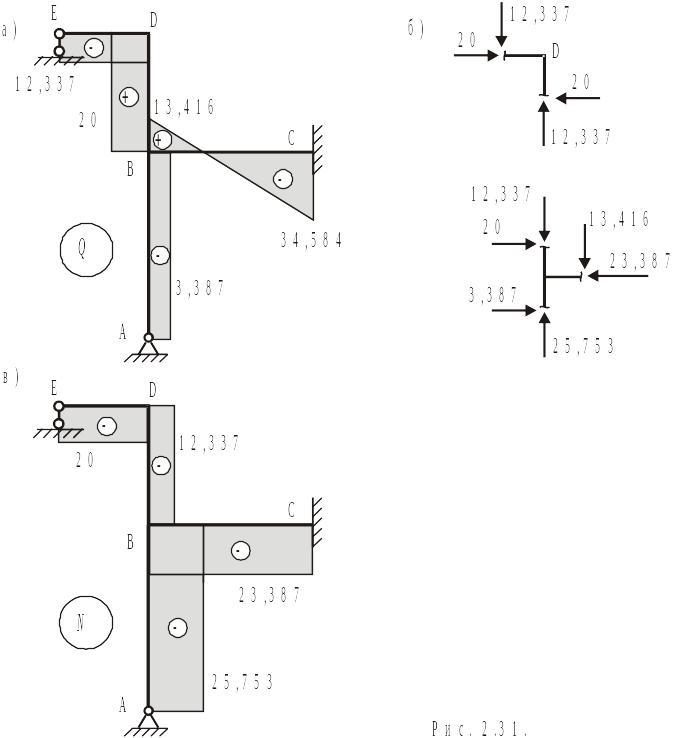
По полученным результатам строим эпюру (рис. 2.31а). Продольные силы (и их действительные направления) определяются из равновесия узлов конструкции (рис. 2.31б). Направления данных сил к узлам конструкции означает сжатие соответствующих участков конструкции. Эпюра показана на рис. 2.31в.