4.4. Вычисление матриц жесткости и векторов нагрузки конечных элементов в глобальной системе координат
В составе конструкции конечные элементы могут располагаться произвольным образом. Поэтому перед включением матрицы жесткости и вектора нагрузки каждого КЭ в матричное уравнение равновесия конечно-элементной модели конструкции данные матрица и вектор должны быть преобразованы к единой для всех КЭ (глобальной) системе координат.
Далее будут использоваться обозначения:
- соответственно матрица жесткости,
вектор узловых перемещений и вектор
нагрузки КЭ в локальной системе координат;
- то же в глобальной системе координат.
Для определения
и
по имеющимся
и
воспользуемся свойством инвариантности
полной потенциальной энергии КЭ по
отношению к различным системам координат:
.
Выражения для
и
имеют вид
Узловые перемещения
и
конечного элемента можно связать
соотношением
,
где
- матрица преобразования, содержащая
направляющие косинусы локальных осей
элемента относительно глобальных осей
координат. Подставляя данное соотношение
в
,
получаем выражение
Из условия
получаем формулы для вычисления матрицы
жесткости
и вектора нагрузки
элемента в глобальной системе координат:
4.5. Формирование матриц преобразования узловых перемещений конечных элементов
ФЕРМЕННЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ
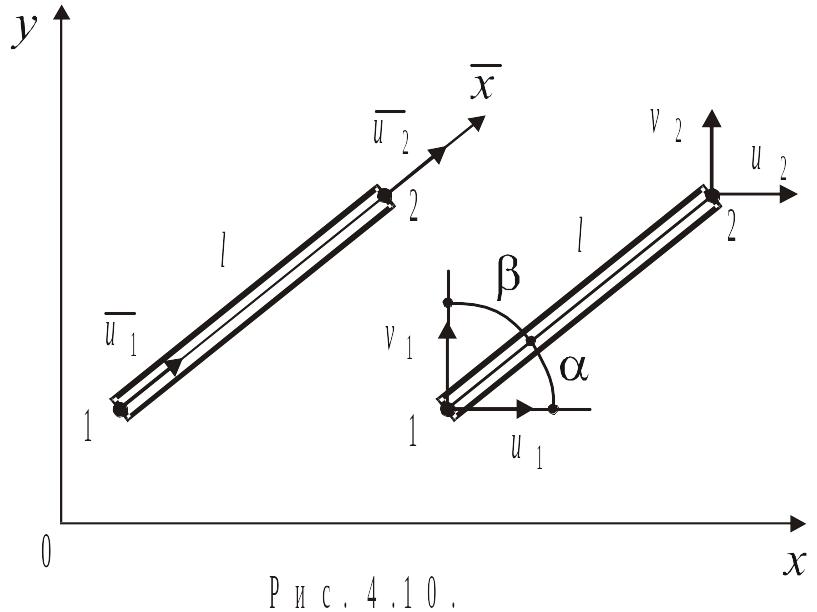
Узловые перемещения ферменного КЭ (рис. 4.10) в локальной и глобальной системах координат связаны соотношениями
Представляя данные соотношения в матричной форме
,
где
получаем матрицу преобразования узловых перемещений ферменного КЭ:
.
Направляющие косинусы локальной оси
вычисляются через глобальные координаты
узлов конечного элемента:
,
(4.5.1)
где
- длина элемента.
БАЛОЧНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ
Связь между узловыми перемещениями балочного КЭ (рис. 4.11) в локальной и глобальной системах координат будет такой:
Данную связь можно представить в виде:
г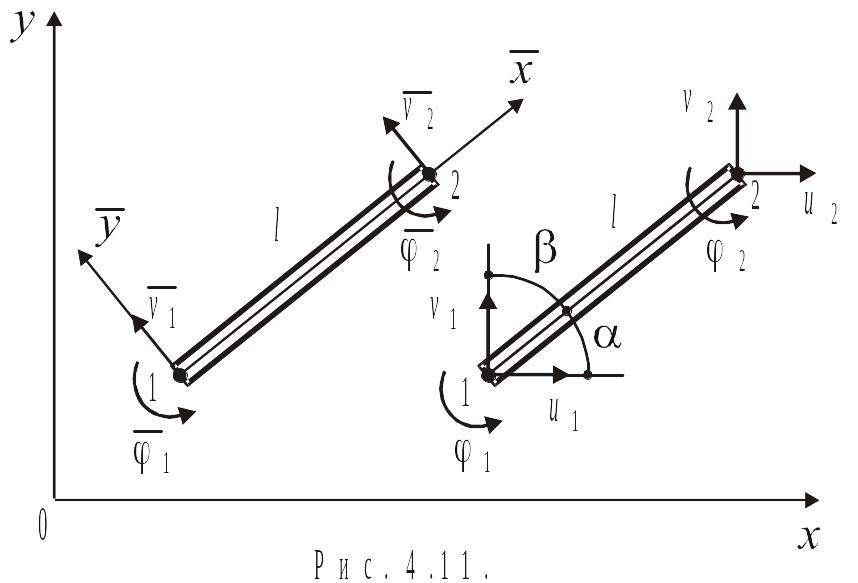
де
Здесь
- матрица преобразования узловых
перемещений балочного КЭ. Направляющие
косинусы локальной оси
вычисляются по формулам (4.5.1).
РАМНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ
Перемещения узлов рамного КЭ (рис. 4.12) в локальной и глобальной системах координат связаны зависимостями
Вводя векторы
и представляя данные зависимости в виде
,
получаем матрицу преобразования
:
Значения
вычисляются по формулам (4.5.1).
ТРЕУГОЛЬНЫЙ КОНЕЧНЫЙ ЭЛЕМЕНТ ПРИ
ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ
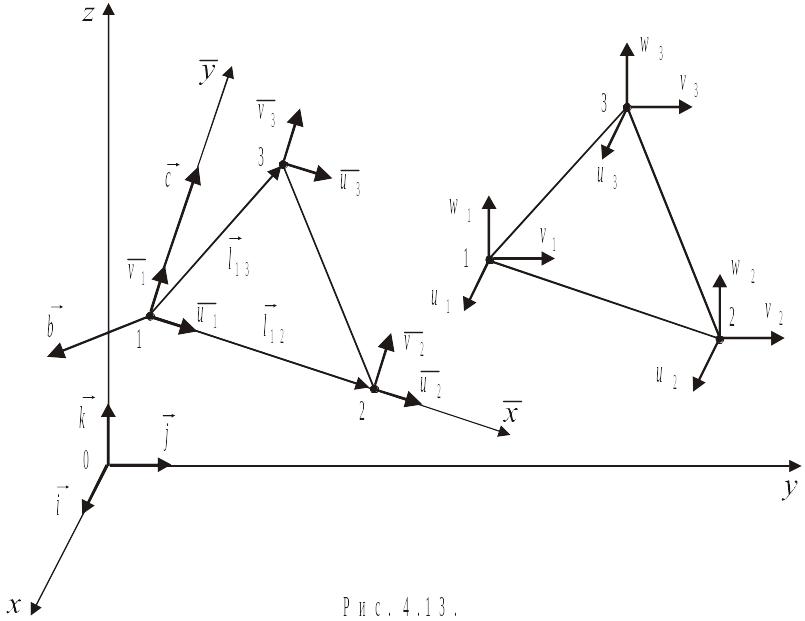
Выберем локальную ось
направленной по стороне 1-2 элемента
(рис. 4.13). Вторая локальная ось
располагается в плоскости элемента.
Связь между перемещениями любого узла
элемента в локальной и глобальной
системах координат имеет вид
.
Здесь
- направляющие косинусы локальных осей
.
Выражения для
можно представить в матричной форме:
,
(4.5.2)
где
.
Тогда связь между узловыми перемещениями
и
в локальной и глобальной системах
координат можно представить в виде
,
где
- матрица преобразования, формируемая
из блоков
:
.
Перейдем к определению направляющих
косинусов, входящих в матрицу
.
Направляющие косинусы локальной оси
определяются непосредственно через
глобальные координаты узлов 1, 2:
.
Здесь
- длина стороны 1-2 элемента. Для определения
направляющих косинусов локальной оси
введем векторы
(рис. 6.4) и найдем векторное произведение:
.
Здесь
- проекции вектора
на глобальные оси
.
Вектор
согласно определению векторного
произведения направлен перпендикулярно
векторам
так, чтобы при виде навстречу данному
вектору вектор
стремился поворачиваться при совмещении
с вектором
на наименьший угол между этими двумя
векторами против хода часовой стрелки.
Далее найдем векторное произведение
векторов
:
,
где
Согласно прежнему определению вектор
получается направленным по локальной
оси
.
Поэтому направляющие косинусы данной
оси совпадают с направляющими косинусами
вектора
:
,
где
- длина вектора
.
Локальные координаты узлов элемента,
необходимые для формирования его матрицы
жесткости
в локальной системе координат, определяются
через глобальные координаты
данных узлов с использованием
преобразования, аналогичного выражению
(4.5.2):
.
При
получаем, как и должно быть,
.