Задание 7. Нахождение максимального потока
Вариант 1.
Найдите оптимальные объемы добычи (узлы 1, 2, 3) и потребления (узлы 11 и 12) газа. Числа у дуг означают пропускную способность труб. Некоторые из труб допускают поток в обе стороны.
Построить математическую модель задачи.
Как изменится потребление, если одна из труб временно законсервирована (выбрать по своему усмотрению).
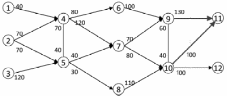
Вариант 2.
Найдите оптимальные объемы добычи (узлы 1, 2, 3) и потребления (узлы 8 и 9) газа. Числа у дуг означают пропускную способность труб. Некоторые из труб допускают поток в обе стороны.
Построить математическую модель задачи.
Как изменится потребление, если одна из труб временно законсервирована (выбрать по своему усмотрению).
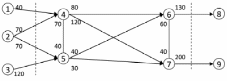
Вариант 3.
Найдите оптимальные объемы добычи (узлы 1, 2, 3) и потребления (узлы 8 и 9) газа. Числа у дуг означают пропускную способность труб. Некоторые из труб допускают поток в обе стороны.
Построить математическую модель задачи.
Как изменится потребление, если одна из труб временно законсервирована (выбрать по своему усмотрению).
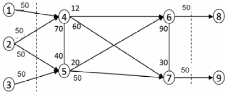
Вариант 4.
Найдите оптимальные объемы добычи (узлы 1, 2, 3) и потребления (узлы 11 и 12) газа. Числа у дуг означают пропускную способность труб. Некоторые из труб допускают поток в обе стороны.
Построить математическую модель задачи.
Как изменится потребление, если одна из труб временно законсервирована (выбрать по своему усмотрению).
Задание №8
Необходимо разработать оптимальную стратегию управления запасами, исходя из имеющейся информации.
Этапы исследования:
1. Случай однопродуктовой модели (номер продукта соответствует варианту), используя аналитический и численный способ решения.
Записать математическую постановку задачи.
Построить график зависимости оптимального объема заказа от интенсивности спроса;
2. Случай 5-ти продуктовой модели (использовать данные для расчета в соответствии с таблицей вариантов)
Записать математическую постановку задачи.
3. Случай 5-ти продуктовой модели с ограничениями на складские помещения (параметры ограничений задать самостоятельно).
Записать математическую постановку задачи.
Данные для расчетов
Параметр |
|
Номер продукта |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
Горизонт планирования, дней |
T |
360 |
360 |
360 |
360 |
360 |
360 |
360 |
360 |
360 |
360 |
Интенсивность спроса шт./день |
D |
6 |
3 |
4 |
5 |
4 |
3 |
5 |
6 |
5 |
6 |
Затраты на партию, у.е. |
соф |
2000 |
150 |
800 |
150 |
2000 |
2500 |
200 |
300 |
400 |
500 |
Затраты на хран. у.е./шт./день |
схр |
1,5 |
1 |
2 |
1 |
4 |
1 |
3 |
2 |
1 |
2 |
Цена без скидки, у.е. |
спр1 |
25 |
12 |
40 |
80 |
100 |
17 |
30 |
40 |
35 |
45 |
Цена со скидкой, у.е. |
спр2 |
23 |
11 |
30 |
75 |
90 |
15 |
40 |
50 |
45 |
55 |
Объем для скидки, шт. |
Q |
200 |
300 |
100 |
400 |
200 |
150 |
200 |
220 |
230 |
240 |
Срок поставки, дней |
L |
10 |
20 |
7 |
5 |
8 |
20 |
10 |
8 |
12 |
8 |
Таблица вариантов
Вариант |
Номера продуктов (для 5-ти продуктовой модели) |
1 |
Все нечетные |
2 |
Все четные |
3 |
1 – 5 |
4 |
6 - 10 |