
Задача №4
Условие задачи: рассчитать и построить асимптотическую ЛАЧХ разомкнутой САУ.
Передаточная функция разомкнутой системы, приведенная к последовательному соединению типовых элементарных звеньев, имеет вид:
Рассчитаем параметры, необходимые для построения асимптотической ЛАЧХ разомкнутой САУ. Определим частоты сопряжения асимптотической ЛАЧХ как величины, обратные постоянным времени звеньев, входящих в состав последовательного соединения:

Определим угол наклона проведения первой асимптоты в частотном диапазоне до первой частоты сопряжения по формуле -20n дБ/дек, где n – степень астатизма разомкнутой САУ. Степень астатизма разомкнутой САУ равна 1, поэтому угол наклона первой асимптоты составит -20 дБ/дек.
Определим высоту проведения первой асимптоты для любой частоты, меньшей первой частоты сопряжения w1, например, для частоты 0.1 Гц:
20lg(k/w)=20lg(1.04/0.11)=20lg(10.4)=20.34 дБ.
В остальных частотных диапазонах угол наклона асимптоты будет определяться типом звена.
-частота сопряжения w1 соответствует дифференцирующему звену первого порядка, которое изменяет наклон ЛАЧХ на +20 дБ/дек, следовательно, с учетом наклона первой асимптоты, в диапазоне от первой до второй частоты сопряжения угол наклона ЛАЧХ составит 0 дБ/дек;
-вторая частота сопряжения соответствует апериодическому звену первого порядка, которое изменяет наклон в своем диапазоне на -20 дБ/дек, следовательно, наклон ЛАЧХ в третьем диапазоне частот составит -20 дБ/дек;
-третья частота сопряжения соответствует дифференцирующему звену первого порядка, которое изменяет наклон в своем диапазоне на +20 дБ/дек, следовательно, наклон ЛАЧХ в четвертом диапазоне частот составит 0 дБ/дек;
-четвертая частота сопряжения соответствует апериодическому звену первого порядка, которое изменяет наклон в своем диапазоне на -20 дБ/дек, следовательно, наклон ЛАЧХ в пятом диапазоне частот составит -20 дБ/дек;
-пятая частота сопряжения соответствует дифференцирующему звену первого порядка, которое изменяет наклон в своем диапазоне на +20 дБ/дек, следовательно, наклон ЛАЧХ в шестом диапазоне частот составит 0 дБ/дек;
Результат построения асимптотической ЛАЧХ имеет вид:
L(),
дБ
,
Гц
80
60
40
20
0
-20
-40
-60
-80
1=0.53
2=2
3=3.19
4=6.25
5=7.58

Как видно, результат построения асимптотической ЛАЧХ достаточно близко совпадает с результатом точного расчета и построения ЛАЧХ, выполненного в Задаче №3.
Задача №5
Условие задачи: оценить устойчивость замкнутой САУ по теореме Ляпунова.
Согласно теореме Ляпунова, для устойчивости САУ необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную действительную часть.
Если известна передаточная функция разомкнутой САУ, то характеристическое уравнение соответствующей ей замкнутой САУ может быть получено как сумма числителя и знаменателя передаточной функции разомкнутой САУ.
Передаточная функция разомкнутой системы, приведенная к последовательному соединению типовых элементарных звеньев, имеет вид:
Запишем характеристический полином замкнутой САУ:
![]()
Введем характеристическое уравнение замкнутой САУ в рабочем поле Mathcad и найдем его корни с помощью символьного оператора Solve (Решить) и пересчитаем ответ в десятичную дробь с точностью до трех значимых цифр в числе, применив символьный оператор Float.
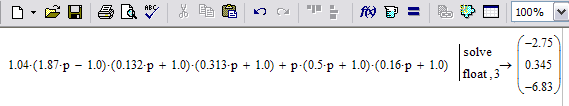
Множество корней характеристического уравнения замкнутой САУ представлено в круглых скобках. Не все корни отрицательны, следовательно, замкнутая САУ является неустойчивой.
