28. Метод абсолютных разниц

Метод абсолютных разниц (MAP) не является самостоятельным методом факторного анализа. Его формулы получены из формул МЦП путем их преобразования. Поэтому с помощью метода абсолютных раз­ниц получаются такие же результаты, что и с помощью метода цепных подстановок. Чтобы получать единообразные результаты, в MAP нужно придерживаться того же порядка записи факторов в мультипликатив­ных и в аддитивных моделях, что и в МЦП. MAP получил широкое распространение, потому что его форму­лы менее трудоемки, чем формулы МЦП.

Дописать формулы

29. Метод относительных разниц

Метод относительных разниц (МОР) получил свое название из-за того, что в его формулах присутствуют относительные приращения факторов, «относительные разницы», которые рассчитываются, как:

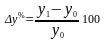; и т. д.

Формулы метода относительных разниц разработаны только для мультипликативных факторных моделей,

МОР обладает теми же свойствами (недостатками), что и МЦП, и МАР: он дает неточные оценки факторов.

Рассмотрим формулы метода относительных разниц на примере модели вида

F = x y z.

Эти формулы имеют вид:

; ; .

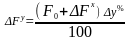По аналогии, можно записать формулы МОР для мультипликативной модели с любым количеством факторов.

По сравнению с методом абсолютных разниц, МОР представляется нам менее удобным. Формулы МАР позволяют оценить влияние любого фактора в модели, независимо от того, рассчитаны ли оценки других факторов. По формулам МОР видно, что влияние каждого следующего в модели фактора можно оценить, только если уже рассчитаны оценки влияния предыдущих ему факторов.

Методом относительных разниц удобно пользоваться в ситуациях, когда для каких-либо целей уже были рассчитаны относительные отклонения факторов. Если при расчете процентных отклонений факторов «вручную» получаются бесконечные десятичные дроби, их приходится округлять.

30. Интегральный метод

Интегральный метод применяется для измерения влияния факто­ров в мультипликативных, кратных и с.меп1анных кратно-аддитивных моделях. Метод называется так потому, что для получения его формул использовалось интегральное исчисление. Интегральный метод позво­ляет получать более точные результаты расчета влияния факторов по сравнению с методами цепных подстановок, абсолютных и относитель­ных разниц, а также некоторыми другими. В интегральном методе эта неточность устраняется за счет того, что дополнительный прирост результативного показателя от взаимодействия факторов делится поровну между всеми факторами. Из-за этого результаты интегрального метода не зависят от местоположения факто­ров в модели. Рассмотрим формулы расчета влияния факторов интегральным методом для двухфакторных и трехфакторных мультипликативных мо­делей. Приведем формулы интегрального метода для мультипликативных моделей. Для двухфакторных моделей

формулы оценок влияния факторов выглядят следующим образом:

или ;

или .

Для трехфакторных моделей

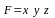
формулы имеют вид:

;

;

.

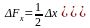Формулы интегрального метода для кратных моделей

имеют вид:

; .

Прямые скобки означают, что выражение под знаком логарифма нужно брать по модулю.

Приведем формулы интегрального метода для смешанных моделей вида

.

Эти формулы имеют вид:

; ; .

Для смешанных моделей вида

формулы интегрального метода – следующие:

; ; ; .

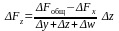интегральный метод точен, дает единообразные результаты, не требует классификации факторов и применим к большинству видов детерминированных факторных моделей, поэтому при решении практических задач анализа нужно отдавать предпочтение именно ему, а не МЦП или МАР.

Заметим, что есть еще более точный метод решения прямой задачи факторного анализа для детерминированных моделей, чем интегральный. Это логарифмический метод. В логарифмическом методе неразложимый остаток распределяется между оценками влияния отдельных факторов не равными частями, а пропорционально силе влияния этих факторов на результирующий показатель.

Логарифмический метод имеет весьма ограниченную область применения, он применим только к мультипликативным факторным моделям, поэтому мы не будем приводить его формулы. Тем не менее, отметим еще одно положительное свойство этого метода. Он дает единообразные результаты при любом порядке факторов в модели, поэтому не требуется их предварительная классификация и расстановка.

Метод получил свое название из-за того, что его формулы получены способом логарифмирования.