1.3. Рабочие вещества холодильных машин

Процессы отвода теплоты от источника низкой температуры, а также подвода теплоты к источнику высокой температуры связаны с явлением теплообмена. Эти процессы протекают с участием не менее двух тел, одно из которых принято называть рабочим телом или хладагентом. Искусственное охлаждение связано с осуществлением термодинамических циклов холодильных машин, которые основаны на фазовых превращениях рабочих веществ. Непрерывный отвод теплоты от охлаждаемого источника возможен, если после совершения холодильного эффекта вернуть рабочее тело в первоначальное состояние. В бытовых компрессионных машинах используются производные углеводородов – фреоны.

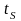Рабочие вещества классифицируют по давлениям и нормальным температурам кипения (при ).

Термодинамические параметры состояния рабочих тел связаны между собой уравнением состояния:

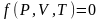
Уравнение состояния Клапейрона справедливо только для идеальных газов. Для реальных газов и паров:

,

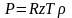где 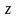– коэффициент сжимаемости, зависящий от безразмерных параметров 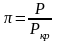; 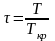( 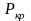, 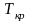– критические давление и температура). Для R–12 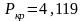МПа; 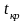=112⁰С; R–22 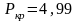МПа; =96,13⁰С. Величины определяются по номограммам.

Широкое распространение получило вириальное уравнение Боголюбова – Майера: ,

где 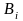- вириальные коэффициенты, зависящие только от температуры. Они имеют физический смысл – характеризуют взаимодействие пары, троек и т.д. до 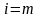молекул. Число вириальных коэффициентов обычно выбирают минимальным. Тогда:

; ,

,

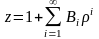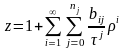где 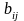- коэффициенты разложения, зависят от свойств рабочих веществ и определяются по экспериментальным данным. Используя уравнения состояния и функциональные зависимости для теплоемкосте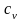й и 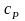, можно определить все термодинамические параметры рабочего вещества.

Термодинамические свойства хладагентов.

Термодинамические свойства рабочих веществ влияют главным образом на эффективность термодинамических циклов, на показатели и характеристики холодильных машин и компрессоров.

Рассмотрим влияние термодинамических свойств рабочих веществ ( , , 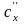и ) на необратимые потери работы при дросселировании и отводе теплоты перегрева при сжатии пара на примере теоретического цикла холодильной машины, – теплота парообразования, – теплоемкость насыщенной жидкости, – теплоемкость насыщенного пара, – изобарная теплоемкость.

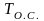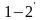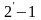При постоянных температурах внешних источников , , бесконечно малой разности температур в процессах теплообмена между рабочим телом и источниками, а также при обратимых процессах сжатия ( ) и ( ) цикл 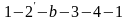имеет только один необратимый процесс дросселирования ( ).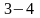

Рис. 1.10. Цикл теоретической холодильной машины с дросселированием и отводом теплоты перегрева при сжатии пара.

Холодопроизводительность цикла 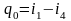эквивалентна площади под процессом ( 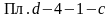). Ее можно представить:

,

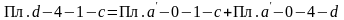где 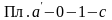соответствует теплоте парообразования при температуре кипения 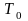, а 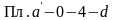соответствует количеству теплоты .

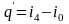Учитывая, что в дроссельном процессе 3–4 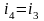получим:

.

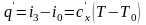Следовательно:

.

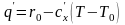Количество теплоты, отведенной от рабочего тела в процессе 2'–3:

,

,

.

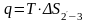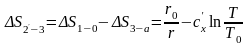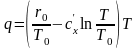Холодильный коэффициент цикла 1–2'–b–3–4–1:

,

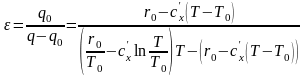или

.

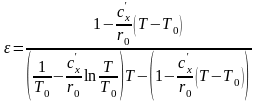Из уравнения следует, что наибольшее значение достигает при максимальном значении теплоты парообразования 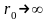и минимальном значении теплоемкости насыщенной жидкости .

В цикле помимо необратимых потерь при дросселировании имеют место необратимые потери, связанные с перегревом пара при сжатии (2'–2). Работа цикла по сравнению с предыдущим циклом при одинаковых холодпроизводительностях возрастает на величину , эквивалентную площади 2–2'–b–2'. Пренебрегая нелинейностью линии 2– b:

,

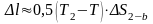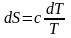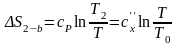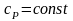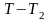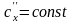т.к. , тогда , интегрируя уравнение при в пределах и в пределах 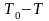, получаем ,

.

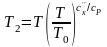Холодильный коэффициент цикла 1–2–3–4–1:

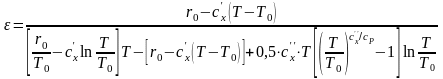
или

.

Из уравнения следует, что наибольшее значение достигает при максимальных значениях теплоты парообразования и изобарной теплоемкости перегретого пара , минимальных значениях теплоемкости насыщенной жидкости и насыщенного пара .

Термодинамические свойства растворов.

В холодильной технике для абсорбционных холодильных машин применяют растворы, состоящие из двух компонентов с разными температурами кипения. Один из компонентов является хладагентом, другой поглотителем рабочего вещества или абсорбентом. Компоненты раствора отличаются нормальными температурами кипения. Наиболее распространенными являются водоаммиачный раствор и раствор бромистого лития в воде.

Массовой концентрацией данного компонента, входящего в раствор, называется отношение его массы к массе раствора.

, , .

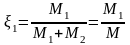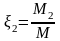Процесс растворения одного из компонентов раствора в другом обычно протекает с выделением или поглощением теплоты. Этот тепловой эффект принято называть теплотой растворения, которая зависит от состояния компонентов до смешения. Полагая, что состояние компонентов ( , 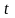) до растворения равно состоянию раствора после их смешения, теплота растворения определяется как разность энтальпий раствора и компонентов перед смешением:

.

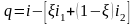Различают интегральную и дифференциальную теплоту растворения. Теплота растворения, полученная при смешении двух компонентов и отнесенная к 1 кг массы раствора, называется интегральной. Дифференциальная теплота растворения – теплота растворения при смешении 1 кг чистого компонента в бесконечно большом количестве раствора при постоянной температуре. Теплота растворения может быть положительной и отрицательной. Если при смешении компонентов теплота выделяется, то – величина отрицательная (теплота отводится) и, наоборот, если при смешении теплота поглощается, то – величина положительная. Если процесс поглощения протекает с выделением теплоты, то:

,

а энтальпия раствора:

.

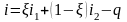Энтальпия раствора может быть выражена через дифференциальную теплоту растворения и :

;

.

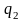Это уравнение определяет связь между интегральной и дифференциальной теплотой растворения.

Для практических расчетов совмещенных циклов абсорбционных холодильных машин используют диаграммы: ; ; ; ; ; .
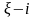
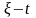
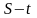
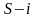