§ 6.5. Характеристики некоторых местных сопротивлений, коэффициент сопротивления системы

В рассматриваемом в данном параграфе материале, относя­щемся к отдельным видам местных сопротивлений, предполага­ется развитый турбулентный режим в области квадратичного со­противления. Движение установившееся, среда несжимаемая. Как уже отмечалось, для абсолютного большинства местных сопротив­лений значения коэффициентов ζ/ определены опытным путем (построены соответствующие таблицы, графики и др.), и только для отдельных сопротивлений простых видов определение ξ/ вы­полнено теоретически с опытной проверкой результатов. Ниже рассмотрена физическая картина и приведены рекомендации для определения коэффициентов сопротивлений только некоторых ме­стных препятствий (внезапного расширения и сужения, диффузора и конфузора, поворотов). В приложении 3 (§ П.3.2) учебника помещены рекомендации по определению коэффициентов сопро­тивлений для ряда видов местных препятствий, что необходимо для выполнения лабораторных работ, расчетно-графических уп­ражнений и курсовых работ. Наиболее полные данные о коэффи­циентах местных сопротивлений приводятся в справочниках [8, 16, 54, 55].

Внезапное расширение

Трубопроводы систем водоснабжения, теплоснабжения, венти­ляции часто в местах смены сечений включают внезапные рас­ширения (рис. 6.4, а). При этом происходит смена меньшего по площади сечения на большее. Поток из трубы меньшего диаметра по переходе сечения внезапного расширения не может сразу рас­шириться и заполнить все пространство в трубе большого диа­метра. Поток постепенно расширяется и заполняет все простран­ство трубы на некотором расстоянии от места смены сечений. Сразу за сечением с внезапным расширением в угловом кольце­вом пространстве имеется вихревая область с вакуумом, наличием воздушных пузырьков. Эту вихревую область, с другой стороны, можно называть застойной, так как жидкость в ней медленно обновляется и только частично участвует в общем движении. Средняя скорость в общем потоке после внезапного расширения уменьшается.

3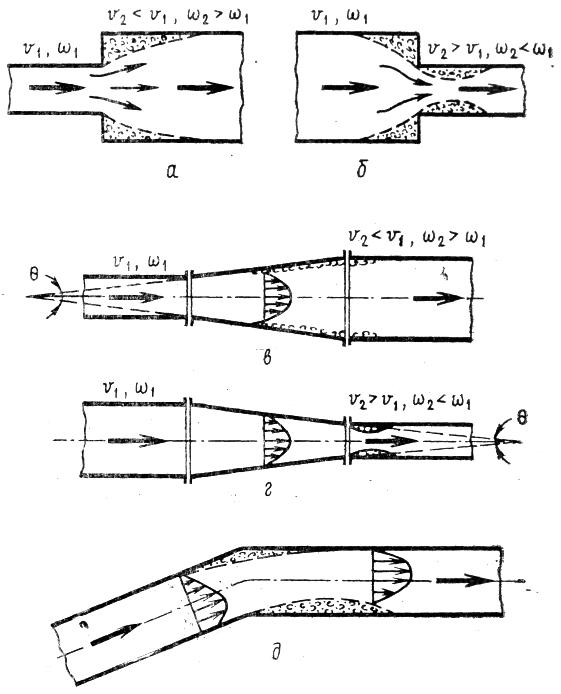

Рис. 6.4

В гидромеханике известна теорема Борда (или Борда — Карно), в соответствии с которой потери напора на внезапном рас­ширении равны скоростному напору потерянной скорости:

(6.31)

где v1 — средняя скорость до, a V₂ — после внезапного расши­рения.

Пусть ω1 — площадь живого сечения потока до, а w2— после внезапного расширения. В соответствии с уравнением неразрывности движения в гидравлической форме должно быть v1w1 = v₂w2. С учетом отмеченного (6.31) преобразуется так:

откуда окончательно (32)

Здесь ξ_ΒΗ.ρ — коэффициент сопротивления внезапного расширения. Формулы (6.31), (6.32) хорошо подтверждаются опытами при раз­витом турбулентном режиме движения. В частном случае течения из трубопровода в резервуар больших размеров нужно принять V₂->0, w2->оо· Тогда по (6.31) потери на выходе из трубопровода

Здесь ksiвых отнесено к скорости перед внезапным расширением. Формула Борда (6.31) преобразуется также в выражение

(6.33)

т. е. потери давления при внезапном расширении равны, динами­ческому давлению, определенному по потерянной скорости.

Формулу (6.31) и выражение для коэффициента ζ_ΒΗ. ρ (6.32) представляют также в виде

,

где α — корректив кинетической энергии. Потери напора на выходе из трубопровода в резервуар h_вых = av1²/2g, ksi_Вых = а. Корректив а= 1,03- 1,10; при больших числах Re в квадратичной области сопротивления можно принимать α =1,0.

Внезапное сужение

При внезапном сужении происходит смена большего по площа­ди сечения на меньшее (рис. 6.4,б). Перед сечением с внезапным сужением линии тока искривляются, струя на начальном участке трубопровода меньшего диаметра сжимается, а далее расширя­ется, заполняя все сечение. Как перед, так и после сечения вне­запного сужения образуются вихревые зоны, жидкость в которых постепенно обновляется. Энергия движущейся среды расходуется на сжатие и расширение потока, вихреобразование, трение. При закруглении кромок на входе в трубу меньшего диаметра потери напора существенно уменьшаются. Потери напора h_bh. _c и коэф­фициент сопротивления местного сопротивления ζ_ΕΗ. _с определя­ются формулами:

(6.34)

Здесь второе выражение есть приближенная полуэмпирическая формула [16]. При выходе трубы из резервуара. (w1->oo, ω₂:ω1 = = 0) коэффициент сопротивления для выхода ζ_Βых = 0,5. Для опре­деления значений ζ_ΒΗ. с в справочниках [16, 54, 55] приводятся более строгие зависимости с построенными по ним таблицами. В заключение следует заметить, что при внезапном сужении потери напора всегда меньше, чем в случае внезапного расшире­ния при одинаковой геометрии перехода, скоростях и др.