§ 6.2. Зависимость коэффициента гидравлического трения от числа рейнольдса и шероховатости, графические представления по опытам для труб с искусственной и технической шероховатостью

Как при ламинарном, так и при турбулентном режимах дви­жения в трубопроводах путевые потери напора определяются фор­мулой Дарси — Вейсбаха

(6.17)

Коэффициент гидравлического трения λ в общем случае является функцией числа Рейнольдса и относительной гладкости (шеро­ховатости) труб, λ=f (Re, r/k). Ho эта зависимость при различ­ных условиях движения разная. При ламинарном режиме движе­ния λ зависит только от числа Рейнольдса Re=vd/v, т. е. от скорости потока, диаметра трубопровода и вязкости жидкости. Пу­тевые потери hf пропорциональны средней скорости в первой сте­пени. При турбулентном режиме движения lam=8g/С², где С —ко­эффициент скорости в формуле Шези; здесь λ зависит в общем случае как от входящих в число Рейнольдса параметров, так и от шероховатости стенок труб.

Коэффициент гидравлического трения при искусственной шероховатости трубопроводов

Первые систематические опытные исследования для определе­ния λ в зависимости от Re и относительной гладкости r/k трубо­проводов в широком диапазоне изменений параметров были вы­полнены И. И. Никурадзе (1933). В результате были построены универсальные графические зависимости (рис. 6.2) в логарифмических координатах. По оси ординат отложены lg 100λ, а по оси абсцисс lg Red. Опыты проводились в диапазоне чисел Re дo 106 и при относительных гладкостях труб r/k= 15-507. Каждой опре­деленной относительной гладкости соответствует отдельный гра­фик. Равномерно распределенная зернистая шероховатость труб создавалась искусственно путем наклейки на внутреннюю поверх­ность труб калиброванного просеиванием кварцевого песка с оп­ределенными размерами частиц. Значения λ вычислялись из (6.17), для чего по данным опытов принимались значения hf, l,

d, v

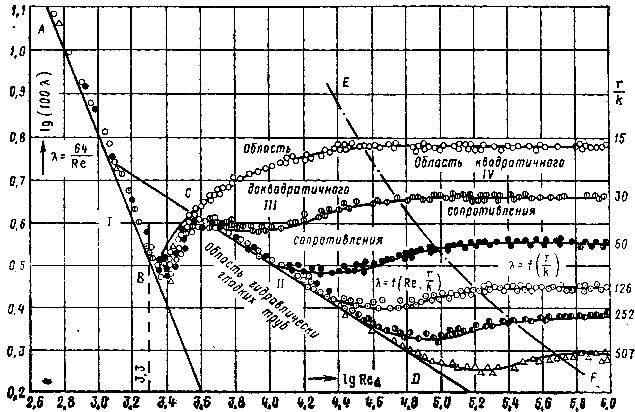
Рис. 6.2

.

На рис. 6.2 имеются: зона ламинарного режима (прямая AB); зона турбулентного режима, включающая в себя области гидравлически гладких труб II (прямая CD), доквадратичного сопротивления III, квадратичного сопротивле­ния IV.

Зона ламинарного режима I. Здесь все опытные точки для труб с разной относительной гладкостью находятся на прямой AB, с предельным значением абсцисс точек до Re = 2300, что соответ­ствует lg Re = 3,36. Следовательно, в этой зоне шероховатость труб не влияет на сопротивление движению и не сказывается на зна­чениях λ, которое здесь равно λ = 64/Re, что ранее было полу­чено теоретически. Потери напора hf пропорциональны средней скорости в первой степени.

Переходной участок BC небольшой, находится в диапазоне чи­сел Re = 2300-4000 (3,3<lgRe<3,6) и соединяет зоны ламинар­ного и турбулентного режимов. Здесь происходит смена режимов движения (участок перемежающейся турбулентности), значения λ существенно увеличиваются. Режим движения неустойчивый, сна­чала в отдельных местах потока возникают и исчезают очаги тур­булентного движения, а затем к концу участка превалирует тур­булентное движение.

Область гидравлически гладких труб II. Эта область относит­ся уже к зоне турбулентного движения. Здесь на участках прямой CD опытные точки для труб разных относительных гладкостей располагаются совместно. Из этого следует, что на этих участках несмотря на турбулентный режим движения коэффициент λ не зависит от шероховатости, а является функцией Lam=f(Re). Чем больше относительная гладкость трубы (т. е. чем меньше шеро­ховатость), тем при больших числах Re происходит срыв с прямой CD графиков, соответствующих разным гладкостям. График для r/k=15 сразу сходит с прямой CD, а график при r/k = 507 схо­дит последним. Совместное расположение на прямой CD точек, соответствующих разным относительным гладкостям, объясняется тем, что при этом толщина δ вязкого (ламинарного) подслоя на стенках трубы больше высоты выступов, δ > k. Происходит без­отрывное обтекание выступов, возмущения от шероховатости га­сятся в ламинарном подслое, общая целостность подслоя не на­рушается. В целом шероховатость стенок не сказывается на зна­чениях λ, турбулентное ядро движется внутри оболочки ламинар­ного подслоя и не имеет контактов с выступами.

G увеличением скоростей в трубе и ростом числа Re значения δ уменьшаются. Отделение графиков с прямой CD начинается с момента, когда становится δ = k. Затем по ходу процесса при δ< <k выступы находятся в контакте с турбулентным ядром, тор­мозят его движение и сказываются на значениях λ. Область II называется областью гидравлически гладких труб, а трубы, экс­плуатирующиеся при δ>k, называются гидравлически гладкими. После отделения графиков от прямой CD δ<k здесь трубы яв­ляются уже шероховатыми. На прямой CD приближенно hf~ ~v^1,75. Используется понятие нижних предельных чисел Рейнольдса как абсцисс точек схода с прямой CD графи­ков, соответствующих различным относительным гладкостям [35]; рекомендуется принимать Red. _пр = 316 (r/k)^0,085.

Область доквадратичного сопротивления III. Эта область огра­ничена слева прямой CD, а справа кривой EF, которая проведена так, чтобы далее за ней графики были параллельными оси абсцисс. Это переходная область от гидравлически гладких труб к области квадратичного сопротивления. Здесь λ=f(Re, r/k), так как каж­дый из семейства графиков, отвечающих определенной относитель­ной гладкости, располагается раздельно, а ординаты их изменя­ются. С увеличением скоростей, а следовательно, и чисел Re тол­щина ламинарного подслоя все более уменьшается, выступы все более проникают в турбулентное ядро, тормозят его движение и влияют на перемешивание в потоке. На самой границе EF лами­нарный подслой находится уже только в углублениях между вы­ступами, с дальнейшим увеличением скоростей он уже уменьшать­ся не может, а графики переходят кривую EF. Область III пере­ходная от гладких труб к совершенно шероховатым, при этом в пределах области hf ~v¹·^75-2.0. Используется понятие верхних предельных чисел Рейнольдса как абсцисс точек пе­ресечений графиков с кривой EF [35]; рекомендуется принимать Re*_d.np = 4160 (r/k)^0.85.

Область квадратичного сопротивления IV. Здесь каждый из семейства графиков располагается также раздельно, имеет раз­ные ординаты в зависимости от относительной гладкости, но все графики параллельны оси абсцисс. В соответствии с этим λ= =f(r/k),т. е. зависит только от относительной гладкости. Здесь значения λ не зависят от числа Re, в том числе и от вязкости жидкости (т. е. от рода жидкости), и при определенных соотно­шениях r/k значения λ постоянные. В рассматриваемой области ламинарный подслой ничтожно мал, так как выступы шерохова­тости взаимодействуют непосредственно с турбулентным ядром. Здесь трубы вполне шероховатые, а путевые потери hf ~ υ².

Коэффициент гидравлического трения при технической шероховатости трубопроводов

Невозможен прямой перенос результатов для труб с искусст­венной шероховатостью на трубы заводского производства, имею­щие техническую шероховатость, обусловленную свойствами ма­териалов и технологией изготовления. В связи с этим у нас и за рубежом выполнены обширные опыты для установления зависи­мостей λ=f(Re, r/k) для изготовляемых промышленностью труб. Из зарубежных наиболее известны исследования К. Кольбрука и Г. Уайта (1938). В СССР систематические опыты для стальных и чугунных труб отечественного производства с технической не­равномерной шероховатостью выполнили Г. А. Мурин (1948) и ф. А. Шевелев (1953). Исследования проводили также И. А. Исаев, П. К. Коыаков, Г. К. Филоненко, H. Ф. Федоров и др. На рис. 6.3 приведено обобщенное графическое представление резуль­татов опытов Г. А. Мурина (Всесоюзный теплотехнический инсти­тут) в координатах λ и Red. Относительная гладкость принята по отношениям d/k.

Рис. 6.3

На чертеже, как и прежде, выделяются области гидравличе­ски гладких труб, доквадратичного и квадратичного сопротивле­ний. В области гидравлически гладких труб в принципе картина аналогична предыдущей. Графики сходят с огибающей практиче­ски прямой линии CD в очередности по соответствию с относитель­ной гладкостью. В переходной области доквадратичного сопротив­ления значения λ зависят как от числа Re, так и от относитель­ной гладкости: Lam=f(Re, d/k). Здесь характерно уменьшение значений λ при увеличении чисел Re. Важно то, что значения λ в этой области больше (но скорости движения меньше), чем далее в области квадратичного сопротивления; это необходимо учиты­вать, если рабочий режим трубопровода попадает в переходную область. В области квадратичного сопротивления графики парал­лельны оси абсцисс и имеют разные ординаты для каждой отно­сительной гладкости, здесь Lam=f(d/k).

Для семейства графиков на рис. 6.3 характерны плавные ли­нии, в том числе на границах между областями. Это объясняется тем, что в трубах промышленного изготовления имеются значи­тельные отклонения высот выступов по отношению к их среднему значению (в трубах с искусственной шероховатостью высоты вы­ступов были практически одинаковыми) и их вершины разновре­менно проникают в турбулентное ядро в ходе уменьшения тол­щины ламинарного подслоя. Этим объясняется плавность схода графиков с линии гидравлически гладких труб, так как момент равенства δ = k четко не выделяется.

Следует отметить также значительные по объему лаборатор­ные опытные исследования открытых безнапорных потоков. Пер­выми и наиболее известными здесь являются опыты А. П. Зегжда (1938) по исследованию зависимостей коэффициента гидравличе­ского трения от числа Рейнольдса, формы и размеров поперечных сечений и шероховатостей стенок каналов. Полученное по данным опытов графическое представление также включает области ла­минарного режима, гидравлически гладких поверхностей, доквадратичного и квадратичного сопротивлений.