2

ГИДРАВЛИЧЕСКИЕ РАСЧЕТЫ ТРУБОПРОВОДОВ

ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОТЕРЬ НА ТРЕНИЕ ПО ДЛИНЕ ПРИ ТУРБУЛЕНТНОМ ДВИЖЕНИИ

Гидравлически гладкие и шероховатые поверхности

Ограничивающие поток твердые стенки имеют в той или иной мере шероховатые поверхности, что связано в первую очередь с материалом стенок, технологией производства и условиями экс­плуатации. Шероховатость оказывает сопротивление движению потока и может быть зернистой, волнистой, зубчатой; она харак­теризуется формой выступов, их размерами и распределением. По­следнее может быть равномерным и неравномерным. Охаракте­ризовать возвышения и углубления на поверхностях стенок коли­чественными показателями затруднительно. Поэтому шерохова­тость поверхности в целом характеризуют некоторой высотой вы­ступов.

Для характеристики шероховатости ограждающих поток по­верхностей используются в первую очередь следующие основные понятия. Абсолютная шероховатость есть средняя вы­сота k выступов. Значения k измеряются в единицах длины (обыч­но в мм). Относительная шероховатость есть отно­шение средней высоты выступов к характерному размеру сечения потока. Так, для трубопроводов это отношение k/r или k/d, где r — внутренний радиус, a d — внутренний диаметр трубопровода. Относительная гладкость есть отношение характерного размера сечения потока к средней высоте выступов (т. е. вели­чина, обратная относительной шероховатости). Так, для трубопро­водов это отношение r/k или d/k.

П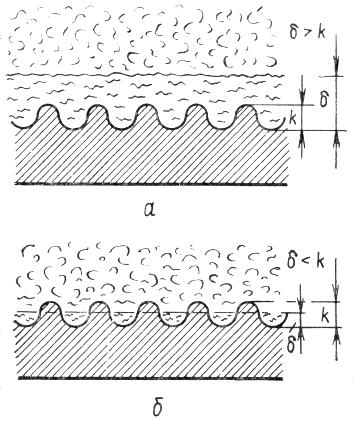 о мере эксплуатации трубопроводов шероховатость их стенок обычно увеличивается из-за коррозии, отложения солей и загряз­нения. Особенно это относится к водопроводам, так как вода хло­рируется и содержит химические реагенты, вследствие чего уси­ливается агрессивность воды по отношению к материалу стенок труб (шероховатость может увеличиваться в два раза и более). В ходе эксплуатации систем теплоснабжения шероховатость тру­бопроводов увеличивается меньше, так как вода менее агрессивна (при обработке умягчается). В целом пар менее агрессивен, чем вода. В газопроводах газ выравнивает стенки, но возможна коррозия стенок, когда газопровод не работает. Значения шеро­ховатости для труб, стенок каналов и т. п. приводятся в спра­вочниках. Например, для стальных новых труб (бесшовных и свар­ных) k = 0,02  0,15 мм, для новых чугунных труб k = 0,2  0,5 мм, для бывших в употреблении стальных и чугунных труб k = 0,2  1,5 мм.

Как уже отмечалось, непосредственно у ограждающих поток поверхностей образуется пристеночный ламинарный (вязкий) под­слой. Пусть  – толщина ламинарного подслоя. В зависимости от соотношений значений  и k влияние шероховатости на сопротивление движению проявляется по-разному. В связи с этим исполь­зуются условные понятия гидравлически гладких и шероховатых поверхностей (рис. 1, а, б). В случае гидравлически глад­ких поверхностей толщина вязкого подслоя больше вы­сот выступов (  > k ). Последние полностью погружены в подслой, так что турбулентная часть потока не имеет контакта со стенка­ми. В трубопроводе турбулентное ядро движется внутри оболочки ламинарного подслоя как по смазке. Потери энергии не зависят от шероховатости. Трубопроводы, работающие при  > k, называ­ются гидравлически гладкими. В случае гидравлически ше­роховатых поверхностей толщина вязкого подслоя меньше высот выступов (  < k ).

В

Рисунок 1

ершины последних входят в турбулентную часть потока, пре­пятствуют его движению и обусловливают потери энергии. Вяз­кий подслой имеется только в углублениях между возвышениями.

Трубопроводы, работающие при  < k, называются гидравлически шероховатыми. Таким образом, одна и та же ограждающая по­ток поверхность может быть как гидравлически гладкой, так и шероховатой, что зависит от соотношения значений  и k.

Формула а. Шези, коэффициент скорости

При развитом турбулентном режиме и установившемся рав­номерном движении для определения средней скорости υ в живом сечении потока имеется формула Шези: (1)

где С – коэффициент скорости (скоростной множитель, коэффи­циент Шези); R — гидравлический радиус живого сечения; I — гидравлический уклон. Формула Шези распространяется на рас­четы напорных и безнапорных потоков, при движениях в реках, каналах, лотках, дренажных и канализационных трубопроводах, а также на расчеты других потоков со свободной поверхностью. Эм­пирический коэффициент скорости С зависит от формы и разме­ров сечений потоков, шероховатости ограждающих поток стенок, рода жидкости. При развитом турбулентном движении коэффи­циент С не зависит от числа Рейнольдса. Размерность С равна корню квадратному из размерности ускорения, обычно м^1/2/с.

Выражение для расхода Q следует после умножения левой и правой частей в (1) на площадь ω живого сечения, так что (2)

Формулы (1) и (2) представляются также в виде: (3)

где (4)

здесь W – скоростная характеристика или модуль скорости (имеет размерность скорости); К – расходная характеристика или модуль расхода (имеет раз­мерность расхода). Физический смысл характеристик W, К сле­дует из (3): W – средняя скорость в живом сечении потока при I = 1; К – расход через живое сечение потока при I = 1.

Из формулы Шези (1), имея в виду, что гидравлический уклон I = h_f / l, где h_f – путевые потери напора, l – длина потока, следует (5)

По этой формуле определяются потери напора в потоках с раз­личной формой поперечных сечений. Как видно, потери напора пропорциональны квадрату средней скорости.

Достоверность расчетов по формулам (1) — (5) связана с точностью значений входящего в формулы коэффициента скоро­сти С. К настоящему времени по результатам огромного количе­ства опытных лабораторных и натурных данных рекомендуются в справочной и другой литературе формульные, гра­фические и табличные зависимости по определению значений С для разнообразных потоков в различных условиях. Известные ре­комендации являются в той или иной мере приближенными и не всегда дают одинаковые значения С в конкретных случаях. На основе обобщения большого количества данных по движению во­ды в каналах и трубах академик H.H. Павловский получил наи­более общую формулу для определения коэффициента С (м^1/2/с) в области квадратичного сопротивления. Эта формула широко при­меняется в нашей стране для гидравлических расчетов и име­ет вид (6)

где R – гидравлический радиус живого сечения в метрах; n – ко­эффициент шероховатости; у – показатель степени, определяемый по общей формуле (7)

Формулу (6) применяют при значениях гидравлического радиуса R < 3,0  5,0 м. Как видно, показатель степени у зависит от гид­равлического радиуса и шероховатости ограждающих поток по­верхностей. Основной диапазон изменений у в пределах ¼  1/7. Для определения показателя степени у рекомендованы также уп­рощенные формулы:

(8)

Численные значения коэффициента шероховатости n также влияют на точность расчетов и зависят от материала и техноло­гии изготовления стенок, загрязнения и др. Достаточно подроб­ные данные значений коэффициента n для различных ограждаю­щих поток поверхностей приводятся в справочниках [8, 54, 55]; значения изменяются в основном диапазоне n = 0,009  0,040 ( 1/n = 111  25 ).

Коэффициент шероховатости n для некоторых поверхностей имеет следующие значения:

Поверхности исключительно гладкие, покрытые эмалью, ме­таллическая гладкая обделка ....…….0,0090,010

Трубы стальные, чугунные и гончарные, новые, хорошо соединенные в швах без стеснения сечения 0,011

Трубы водопроводные в обычных условиях эксплуатации и загрязненные 0,012  0,014

Трубы и облицовка каналов из бетона и железобетона с тщательной затиркой 0,012  0,016

Облицовка каналов бетоном и железобетоном с торкретированной поверхностью 0,016  0,025

Из общего выражения (6), как частные, следуют другие ра­нее известные формулы для определения С, а именно: 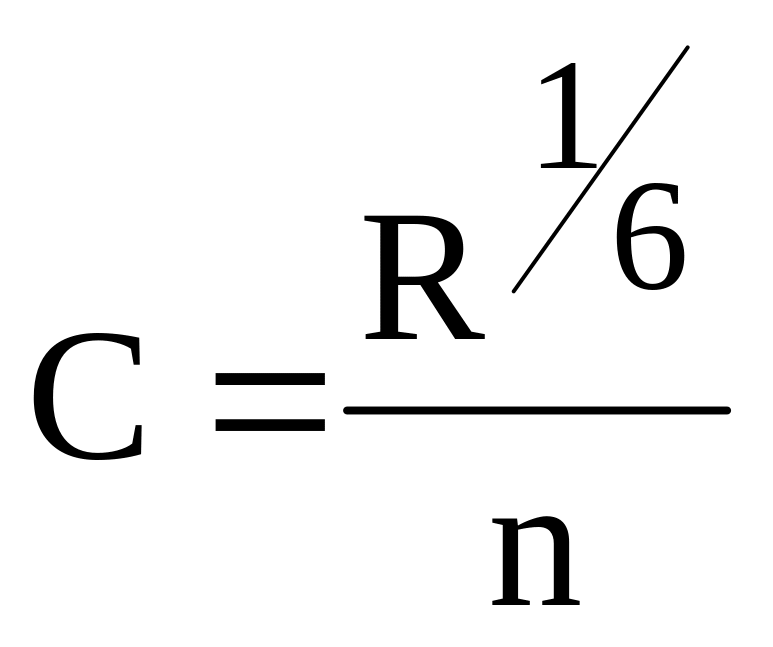(a); 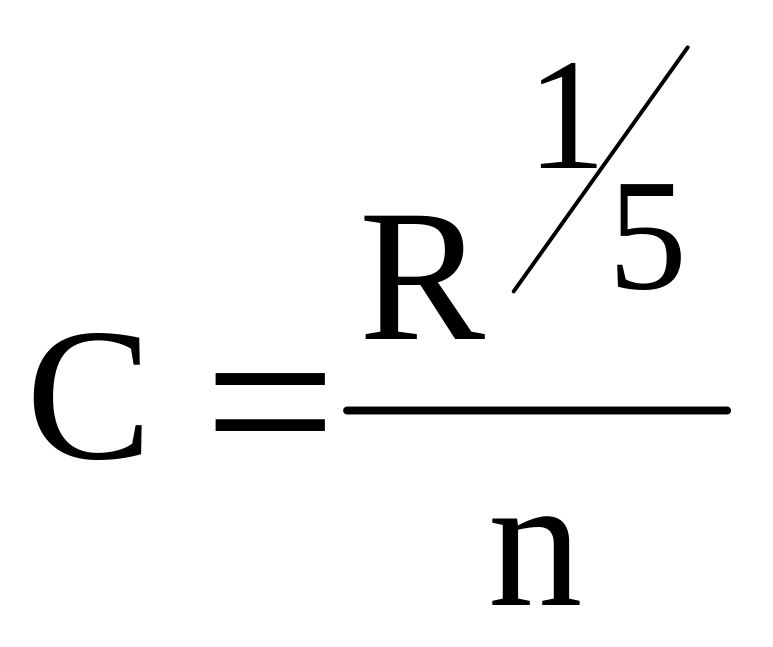(b) (9)

Здесь первая (а) есть известная формула Маннинга (у= 1/6), а вторая (b) есть формула Форхгеймера (у= 1/5).

Для открытых русл представляет интерес обобщенная фор­мула А. Д. Альтшуля для всех зон турбулентного режима дви­жения воды (квадратичной, переходной и области гладких русл)

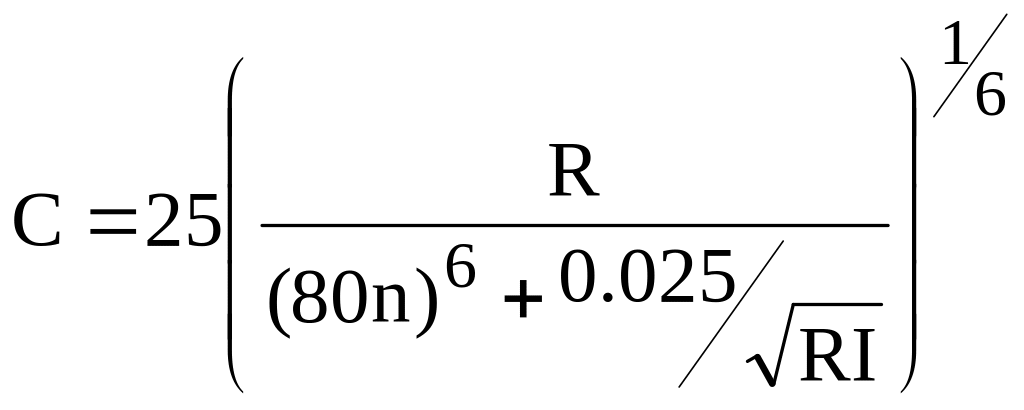(м²/с), (10)

где R — гидравлический радиус, мм; n — коэффициент шерохова­тости; I — гидравлический уклон. При развитом турбулентном дви­жении и квадратичном сопротивлении произведение RI большое и выражение (10) дает результаты, близкие к данным по фор­муле Маннинга. При гладких руслах (RI и n малые) результаты расчетов близки к данным по известной формуле Блазиуса. В спра­вочной литературе читатель может ознакомиться с рекомендация­ми для определения С других авторов (И.И. Агроскина, Б. Базе-на, К. Гангилье — Куттера, В. H. Гончарова, П. Ф. Горбачева и др.).

Потери напора (давления) в трубопроводах на трение по длине

Целесообразно отдельно рассмотреть вопрос о потерях напора в круглоцилиндрических напорных трубопроводах. Для этого в формуле (5) нужно заменить гидравлический радиус (R=d/4), а также умножить числитель и знаменатель на 2g (d — диаметр, g — ускорение свободного падения). Тогда

. (11)

Далее с учетом того, что h_f = p/, расчетная формула для опре­деления потерь напора (давления) при турбулентном режиме в круглых напорных трубопроводах записывается в следующем окон­чательном виде (формула Дарси — Вейсбаха): . Здесь p — перепад давления в трубопроводе на длине l, γ — удельный вес жидкости, а λ — коэффициент гидравличе­ского трения по длине при турбулентном режиме движения:  =8g/C², (12)

Коэффициент λ — безразмерный, эмпирический и связан с ко­эффициентом скорости С этими зависимостями. В общем случае коэффициент λ зависит от формы и размеров трубопровода, от­носительной шероховатости и числа Re (учет скорости, вязкости). При развитом турбулентном режиме λ от Re не зависит. Значе­ния λ приводятся в справочниках в зависимости от диаметров тру­бопроводов и шероховатости материала труб.

Из основной расчетной формулы (11) следует, что при тур­булентном режиме движения путевые потери напора h_f (потери давления p) пропорциональны длине трубопровода и квадрату средней скорости; с увеличением диаметра потери энергии умень­шаются (диаметр находится в знаменателе формулы и, кроме то­го, λ зависит от диаметра). Формула (11) по внешнему виду такая же, как и формулы для определения потерь напора (дав­ления) при ламинарном режиме. Однако при лами­нарном режиме путевые потери пропорциональны средней скоро­сти в первой степени, а коэффициент λ зависит только от числа Рейнольдса (L=64/Re).

При практических расчетах круглых трубопроводов (в обла­сти квадратичного сопротивления) наряду с основной формулой (6.11) применяется также другая расчетная формула, которая сле­дует из (11) после умножения числителя и знаменателя на квад­рат площади живого сечения, т. е.

или в окончательном виде (a); (b). (13)

Здесь коэффициент К имеет размерность расхода и называется, как и прежде (4), расходной характеристикой или модулем рас­хода. Значения К² приводятся в справочниках. Выражение (13, а) иногда называют водопроводной формулой. Очевидно, что форму­ла (13, a) следует непосредственно также из (3).

При расчетах трубопроводов применяется еще одна модифи­кация расчетных формул, в связи с чем используются обозна­чения: S₀ = l/K²; S = S₀l, (14)

где S₀ – удельное сопротивление; S – сопротивле­ние трубопровода.

С учетом этих обозначений расчетная формула (13, а) не­сколько видоизменяется:

h_f = S₀Q²l=SQ², I=S₀Q². (15)