21)Теорема об изменении главного момента количества движения системы (кинетического момент системы). Закон сохранения кинетического момента.

Главным моментом количеств движения системы (ГМКДС) или кинетическим моментом относительно данного цент­ра О называется величина , равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра (6.25)

Аналогично  имеем относительно координатных осей

,     ,    .    (6.26)

Теорема об изменении ГМКДС (теорема мо­ментов): производная  по времени от ГМКДС относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относитель­но того же центра Проецируя на неподвижные оси 0хyz, получим теорему в проекциях.

Теорема применяется для изучения враща­тельного движения тела, а также движения системы в общем случае, т.к. последнее слага­ется из поступательного и вращательного движения. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изучена с помощью теоремы о движении центра масс, а вращательная - с помощью теоремы моментов. При этом из рассмотрения исключаются наперед неизвестные внутренние силы.

Для системы координат, движущейся поступательно вместе с телом, справедлива теорема моментов относительно его центра масс. Она имеет тот же вид, что и относительно неподвижного центра. Для моментов относительно осей такой системы также получаются схожие урав­нения.

Следствие из теоремы (закон сохранения ГМКДС): внутренние силы не изменяют ГМКДС. При этом если система неизменяема, то она  вращается с постоянной угловой скоростью, а если изменяема, то под действием внутренних (или внешних) сил расстояния отдельных ее точек от оси могут изменяться, что вы­зовет изменение угловой скорости.

22)Кинетическая энергия системы. Вычисление кинетической энергии тела при посту нагельном, вращательном и плоскопараллельном движениях. Теорема об изменении кинетической энергии системы. Кинетическая энергия системы – скалярная величина Т, равная арифметической сумме кинетической энергий всех точек системы: .

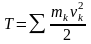Кинетической энергией (КЭ) системы называют скалярную величину .                    КЭ является характеристикой и поступатель­ного, и вращательного движений системы. Отличие Т от  и  состоит в том, что КЭ является скалярной су­щественно положительной величиной, не зависящей от направлений движения частей МС, и не характеризует их изменение. Внутренние силы действуют на части системы по взаимно противоположным на­правлениям, поэтому они не изменяют векторные величины  и . Но если под действием внутренних сил будут изменяться модули скоростей точек системы, то при этом будет изменяться и величина Т. Т.о., T отличается от величин  и  еще и тем, что на ее изме­нение влияет действие и внешних, и внутренних сил. КЭ тела в частных случаях движения:

а) при поступательном движен ,  б)  при вращательном движении ,      

в) при плоскопараллельном  движении  

Теорема об изменении КЭ сиcтемы в дифферен­циальной форме

В интегральной форме: изменение КЭ системы при некотором перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внут­ренних сил.

.