7. Методи фазифікації.

Блок фазіфікації перетворює чіткі величини, виміряні на виході об'єкта керування, у нечіткі величини, що описані лінгвістичними змінними в базі знань.

Отже, головними задачами фазифікації є перевірка нечітких діапазонів на припустимість, відображення контрольованих величин у вигляді нечітких діапазонів і представлення отриманих результатів для інформації (агрегування, імплікації, акумулювання), тобто логічної обробки.

8. Структура бази знань в регуляторах на основі нечіткої логіки.

Правила містять знання експертів про те, що треба роботи, якщо стала справедливою одна з властивостей, сформульованих при фазифікації. Правила регулюють взаємозв’язки даних фазифікації з даними логічної обробки і являють собою чіткі висловлювання. Операції “ЯКЩО (умова) ТО (дія)” працюють з нечіткими даними, тому, хоча правила і є чіткими, результат можна отримати тільки нечіткий.

Проте, для складання бази правил не існую жодного систематизованого алгоритму, тому цей етап проектування фаззі-регулятора не має такої загальноприйнятної систематики, як при проектуванні класичних результатів. Це ускладнює процес проектування і тому, як наслідок, трапляються випадки, коли різні настройки фаззі-блоку зумовлюють майже ідентичні його передавальні властивості [5]

9. .Методи нечіткого висновку.

Нечіткий логічний висновок - Основою для його проведення є база правил, яка містить нечіткі висловлювання у формі "Якщо щось" і функції приналежності для відповідних лінгвістичних термів.

Нечіткий логічний висновок - Включає чотири етапи: введення нечіткості (фазифікація), нечіткий висновок, композиція і приведення до чіткості, або дефазифікації

Процес нечіткого логічного висновку починається з виділення множини

діагностичних ознак, які складаються з множини відповідних характеристик [6]:

(4)

На основі множини DZ визначається множина припущень експерта про можливість

наявності тієї чи іншої несправності:

(5)

Множина припущень групи експертів:

Можлива причина несправності визначається шляхом відбору припущень з

функціями належності, які мають ступені впевненості більші або рівні 0,7:

(7)

На основі (7) формується множина можливих причин несправностей:

(8)

де n – кількість можливих причин несправностей.

Якщо n > 5 , то можливу причину необхідно уточнити шляхом визначення

діагностичних ознак 2-го РВП. У випадку коли ознаки 1-го та 2-го рівнів не привели

до виявлення можливих причин несправностей, то уточнення проводять за допомогою

ознак 3-го РВП.

10. Методи дефазифікації.

Дефаззіфікації - це процес вибору представницького елемента нечіткого виходу С, виведеного з алгоритму нечіткого управління.

11. Методи синтезу регуляторів на основі нечіткої логіки.

12. Методи реалізації регуляторів на основі нечіткої логіки.

13. Біологічний прототип штучної нейронної мережі.

Аналогія з біологічною нейронною мережею. Нервова система і мозок людини складаються з нейронів, з'єднаних між собою нервовими волокнами. Нервові волокна здатні передавати електричні імпульси між нейронами. Кожен нейрон (рис. 5.1), має відростки нервових волокон двох типів – дендрити, по яких приймаються імпульси, і єдиний аксон, по якому нейрон може передавати імпульс. Аксон контактує з дендритами інших нейронів через – синапси, що впливають на силу імпульсу.

Можна вважати, що при проходженні синапса сила імпульсу міняється у визначене число раз, це прийнято називати вагою синапса. Імпульси, що надійшли до нейрона одночасно по декількох дендритах, сумуються. Якщо сумарний імпульс перевищує деякий поріг, нейрон збуджується, формує власний імпульс і передає його далі по аксону. Важливо відзначити, що ваги синапсів можуть змінюватися, а значить, міняється і поводження відповідного нейрона.

Неважко побудувати математичну модель описаного процесу (рис. 2).

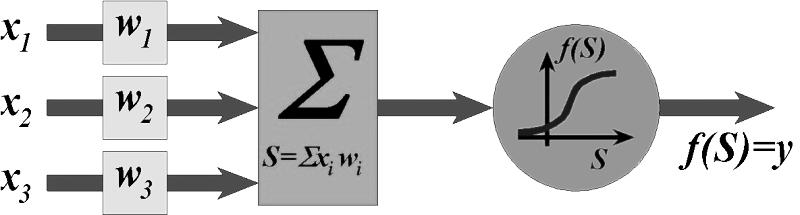
Рис. 5.2. Модель нейрона з трьома входами

На рис. 5.2 зображена модель нейрона з трьома входами (дендритами), причому синапси цих дендритів мають ваги w₁, w₂, w₃. Нехай до синапсів надходять імпульси сили x₁, x₂, x₃ відповідно, тоді після проходження синапсів і дендритів до нейрона надходять імпульси w₁x₁, w₂x₂, w₃x₃. Нейрон перетворює отриманий сумарний імпульс S=w₁x₁+ w₂x₂+ w₃x₃ відповідно до деякої передатної функції (функції активації) f(S). Сила вихідного імпульсу дорівнює y=f(S)=f(w₁x₁+ w₂x₂+ w₃x₃).

Таким чином, нейрон цілком описується своїми вагами w_k і передатною функцією f(x). Одержавши набір чисел (вектор) x_k як входи, нейрон видає деяке число y на виході.

14. Моделі штучних нейронів.

15. Функції активації

16. Штучні нейронні мережі і їх характеристики.

17. Методи навчань штучних нейронних мереж.

Мережа навчається, щоб для деякої множини входів X давати бажану множину виходів Y. Кожна така вхідна (або вихідна) множина розглядається як вектор. Навчання здійснюється шляхом послідовного пред'явлення вхідних векторів з одночасним налагодженням ваг відповідно до певної процедури. В процесі навчання ваги мережі поступово стають такими, щоб кожен вхідний вектор виробляв вихідний вектор. Розрізняють алгоритми навчання з вчителем і без вчителя, детерміновані і стохастичні.

Навчання з вчителем. Навчання з вчителем припускає, що для кожного вхідного вектора X існує цільовий вектор Y^T, що є необхідним виходом. Разом вони називаються навчальною парою. Звичайно мережа навчається для деякої кількості таких навчальних пар (навчальної множини). В ході навчання зчитується вхідний вектор X, обчислюється вихід мережі Y і порівнюється з відповідним цільовим вектором Y^T, різниця D ~ Y^T – Y за допомогою зворотного зв'язку подається в мережу і змінюються ваги W відповідно до алгоритму, прагнучого мінімізувати помилку ε. Зчитування векторів навчальної множини і налагодження ваг виконується до тих пір, поки сумарна помилка для всієї навчальної множини не досягне заданого низького рівня.