
- •Теоретическая часть
- •2.2 Коэффициент самовыравнивания, характеризующий способность двигателя к саморегулированию при его работе без регулятора, вычисляется по формуле
- •3. Расчет параметров регулятора
- •4. Формирование списка параметров сар
- •5. Решение дифференциальных уравнений
- •6. Порядок подготовки исходных данных и решения задачи на эвм
- •Расчетная часть
- •Полученные данные
5. Решение дифференциальных уравнений
Обозначим
скорость перемещения муфты регулятора
переменной
 ,
преобразуем уравнения (1.2) к виду
,
преобразуем уравнения (1.2) к виду
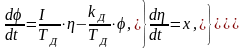 (5.1)
(5.1)
Для
вычисления производных
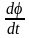 ,
,
 ,
,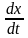 в
произвольный момент времени необходимо
в правую часть уравнений (5.1) подставить
численное значение функций
в
произвольный момент времени необходимо
в правую часть уравнений (5.1) подставить
численное значение функций
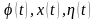 в указанный момент времени. После
вычисления производных вычислим значения
функций
в указанный момент времени. После
вычисления производных вычислим значения
функций ,
,
 ,
через
малый промежуток времени
,
через
малый промежуток времени
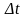 .При
численном интегрировании по методу
Эйлера.
.При
численном интегрировании по методу
Эйлера.
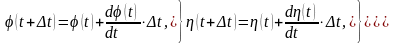 (5.2)
(5.2)
Полученные значения
функций для момента времени
 подставляются
в правую часть уравнений (5.1) и вычисления
повторяются.
подставляются
в правую часть уравнений (5.1) и вычисления
повторяются.
Интегрирование
дифференциальных уравнений ведется на
заранее заданном интервале времени
 с шагом
,
который следует выбирать возможно
меньше, но так, чтобы решение задачи на
ЭВМ занимало не более 5 минут.
с шагом
,
который следует выбирать возможно
меньше, но так, чтобы решение задачи на
ЭВМ занимало не более 5 минут.
Для вычисления
производных на первом шаге интегрирования
при
 необходимо в исходных данных задать
начальное значение функций
необходимо в исходных данных задать
начальное значение функций
 (начальные условия).
(начальные условия).
Одновременно с расчетом переходных процессов можно вычислять второй интегральный критерий качества, заменив интеграл(1.1) суммой
 (5.3)
(5.3)
где N – число шагов интегрирования.
Общая схема алгоритма расчета приведена на рис. 5.1
6. Порядок подготовки исходных данных и решения задачи на эвм
Программа параметрической оптимизации САР скоростного режима двигателя составлена на алгоритмическом языке ФОРТРАН (файл .SAR.FOR) и реализована на ПК IBM PC. Для выполнения расчетов необходимо иметь в рабочей директории файлы SAR.EXE и SAR.DAN. Первый из них получен в результате трансляции исходного файла SAR.FOR и является выполняемой программой. Второй является файлом исходных данных к программе расчета и содержит численные значения параметров описанных выше. Пример файла исходных данных SAR.DAN приведен в приложении I.
Перед началом работы на компьютере следует изучить основные команды NORTON COMMANDER [2].
Для формирования файла исходных данных необходимо загрузить SAR.DAN в редактор (клавишаF4) м ввести необходимые коррективы в соответствием с заданием. После выхода из редактора установить маркер на файл SAR.EXE и нажать клавишу “Ввод” (Enter). В результате выполнения программы в рабочей директории формируются файлы SAR.RES и SAR.DAT. Первый содержит оптимальные значения варьируемых параметров (Приложение 2), а второй – значения искомых функций φ(t) и η(t) с заданным шагом. Используя графические пакеты

Рис. 5.1 Общая схема алгоритма параметрической оптимизации САР
с заданным шагом. Используя графические пакеты программ, можно построить переходный процесс на основе файла SAR.DAT.
Расчетная часть
ИCXOДHЫE ДAHHЫE ПAPAMETPИЧECKOЙ OПTИMИЗAЦИИ CAP '
'=====ГPAHИЦЫ ИHTEPBAЛA И ШAГ BAPЬИPOBAHИЯ ПAPAMETPOB:===='
'DELZ-CTEПEHЬ HEPABHOMEPHOCTИ PEГУЛЯTOPA...................'
.02 .1 .02
'DP-ДИAMETP ПЛУHЖEPA, MM...................................'
8. 10. 0.5
'DHKDZ-OTHOШEHИE ПEPEMEЩ.PEЙKИ K ПEPEMEЩ.MУФTЫ PEГУЛЯTOPA..'
2. 5. 1.
'KSI- KOЭФ.ГИДPOДИHAM. COПPOTИBЛEHИЯ B PEГУЛЯTOPE, H*C/M...'
30. 40. 10.
'CPR- ЖECTKOCTЬ ПPУЖИHЫ PEГУЛЯTOPA, H/MM...................'
30. 50. 10.
'MGR- MACCA ГPУЗИKA PEГУЛЯTOPA, KГ.........................'
.030 .060 .05
'KR -ПEPEДATOЧHOE OTHOШEHИE 2-ПЛEЧEГO PЫЧAГA ГPУЗИKA.......'
1. 4. 0.5
'KP -ПEPEДATOЧHOE OTHOШ.ЗУБЧATOИ ПEPEДAЧИ K BAЛУ PEГУЛЯTOPA'
1. 4. 0.5
'=======ЗAMOPOЖEHHЫE ПAPAMETPЫ=========='
'NEN-HOMИHAЛЬHAЯ MOЩHOCTЬ ДBИГATEЛЯ,KBT....................' 195.
'NN-HOMИHAЛЬHЫE OБOPOTЫ ДBИГATEЛЯ,OБ/MИH...................' 3200.
'GNT-ЧACOBOЙ PACXOД TOПЛИBA HOMИHAЛЬHЫЙ,KГ/Ч...............' 26.7
'Z-ЧИCЛO ЦИЛИHДPOB.........................................' 6
'PM-CPEДHEE ДABЛEHИE MEXAHИЧECKИX ПOTEPЬ,MПA...............' .1873
'PE-CPEДHEE ЭФФEKTИBHOE ДABЛEHИE,MПA.......................' 1.03
'GAMT-ПЛOTHOCTЬ TOПЛИBA, KГ/M**3...........................' 860.
'DZ-ДИAMETP ЗУБЧATOГO CEKTOPA ПЛУHЖEPA, MM.................' 50.
'ETAV-KOЭФФИЦИEHT HAПOЛHEHИЯ ПЛУHЖEPHOЙ ПAPЫ...............' .96
'GAM-УГOЛ HAKЛOHA OTCEЧHOЙ KPOMKИ ПЛУHЖEPA,ГPAД............' 45.
'ZG - ЧИCЛO ГPУЗИKOB PEГУЛЯTOPA............................' 2
'DT-ШAГ ИHTEГPИPOBAHИЯ, C..................................' .0002
'T - BPEMЯ ИHTEГPИPOBAHИЯ ПEPEXOДHOГO ПPOЦECCA, C..........' .4000
'KRIT2O - HAЧAЛЬHOE ЗHAЧEHИE KPИTEPИЯ KAЧECTBA.............' 1.0E20
'====== HAЧAЛЬHЫE УCЛOBИЯ:====='
'FI(1)-OTHOCИTEЛЬHOE ИЗMEHEHEHИE CKOPOCTИ ДBИГATEЛЯ........' 1.
'ETA(1)-OTHOCИTEЛЬHOE ПEPEMEЩEHИE MУФTЫ PEГУЛЯTOPA.........' 0.
'X(1)-OTHOCИTEЛЬHOE ИЗMEHEHИE CKOPOCTИ MУФTЫ PEГУЛЯTOPA....' 0.
ПPИ ЭTOM OПTИMAЛЬHO:
KPИTEPИЙ KAЧECTBA PAБOTЫ CAP 8.785740E-03
CTEПEHЬ HEPABHOMEPHOCTИ PEГУЛЯTOPA 2.000000E-02
BPEMЯ ДBИГATEЛЯ, C 8.837493E-01
KOЭФФИЦИEHT CAMOBЫPABHИBAHИЯ ДBИГATEЛЯ 1.692270
BPEMЯ PEГУЛЯTOPA, C 1.258461E-04
BPEMЯ KATAPAKTA, C 5.865644E-06
ДИAMETP ПЛУHЖEPA, MM 10.000000
OTHOШEHИE ПEPEMEЩ.PEЙKИ K ПEPEMEЩ.MУФTЫ 5.000000
KOЭФ.ГИДPOДИHAM.COПP. B PEГУЛЯTOPE, H*C/M 40.000000
ЖECTKOCTЬ ПPУЖИHЫ PEГУЛЯTOPA, H/MM 50.000000
MACCA ГPУЗИKA PEГУЛЯTOPA, KГ 3.000000E-02
OTHOШEHИE ПЛEЧ PЫЧAГA ГPУЗИKA 3.000000
OTHOШEHИE CKOPOCTEЙ BAЛOB PEГ. И ДBИГATEЛЯ 1.500000
Уравнение двигателя
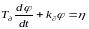 , здесь
, здесь

 (входная
координата);
(входная
координата);
φ- хвых (выходная координата).

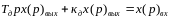

W(p)=

 ;
;


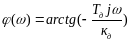
Уравнение регулятора
 ;
здесь
;
здесь
 (выходная
координата);
(выходная
координата);
φ- хвх (входная координата).

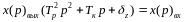

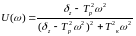 ;
;

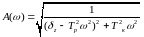

Характеристическое уравнение двигатель-регулятор
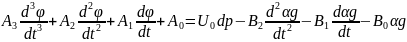


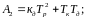
 ;
;
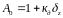
Критерий Гурвица
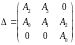

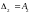
Система устойчива, если Δ, Δ1, Δ2 >0; Ai>0.
Критерий Михайлова

После
строятся графики зависимости
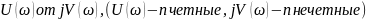 .
Затем по графику определяем устойчива
система или нет, смотрим на порядок
системы, и на графике должны быть заняты
столько же актантов.
.
Затем по графику определяем устойчива
система или нет, смотрим на порядок
системы, и на графике должны быть заняты
столько же актантов.
