Министерство науки и образования РФ

Волгоградский Государственный Технический Университет

Кафедра «Автотракторные двигатели»

Семестровая работа

Параметрическая оптимизация САР скоростного режима двигателя

Выполнил: Студент гр. Д-503 З

1111111111111111

Проверил: Курапин А.В.

Волгоград 2011

Теоретическая часть

1. Постановка задачи

Функцией цели параметрической оптимизации является второй интегральный критерий качества, вычисляемый в виде функционала:

(1.1)

где - относительная скорость вращения вала двигателя в переходом процессе за время регулирования Т.

Основой для расчета в переходном процессе являются дифференциальные уравнения системы автоматического регулирования (САР) скоростного режима двигателя:

(1.2)

где -время двигателя;

- коэффициент самовыравнивания двигателя;

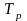- время регулятора;

- время катаракта;

- местная степень неравномерности регулятора;

- относительное перемещение муфты регулятора.

Первое уравнение описывает изменение угловой скорости коленчатого вала двигателя в процессе ее регулирования, второе - перемещение муфты регулятора. Связь уравнений двигателя и регулятора через переменные и показывает, что для высокого качества работы САР каждому сочетанию параметров двигателя ( , и ) необходимо подобрать оптимальное сочетание параметров регулятора ( , , ), при котором второй интегральный критерий качества, вычисляемый по формуле (I.I), будет иметь минимум.

2. Расчет параметров двигателя

2.1. Время двигателя , характеризующие инерционные свойстве кривошипно-шатунного механизма (КШМ), вычисляется по формуле:

(2.1)

где - момент инерции КШМ, кг·м²;

- коэффициент усиления крутящего момента двигателя по перемещению муфты регулятора, Нм/мм;

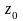- координата муфты регулятора на номинальном режиме, мм;

- номинальная угловая скорость коленвала двигателя, с^-1.

Для вычисления используется эмпирическая зависимость

(2.2)

где 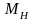- номинальный крутящий момент двигателя, М·н.

(2.3)

(2.4)

где - номинальная мощность, кВт;

- скоростной ренин двигателя, мин^-1.

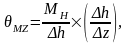(2.5)

где

- отношение перемещения рейки топливного насоса к перемещению муфты регулятора .

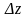Перемещение рейки топливного насоса

(2.6)

где - координата рейки на номинальном режиме, мм;

- координата рейки на режиме максимальных оборотов холостого хода, мм.

(2.7)

(2.8)

где , 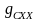- подачи топлива на режимах номинальном и холостого хода, мм³/цикл;

- диаметр зубчатого сектора плунжерной пары, мм;

- диаметр плунжера, мм;

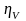- коэффициент наполнения плунжерной пары;

- угол наклона отсечной кромки плунжера, град (см. рис. 2.1).

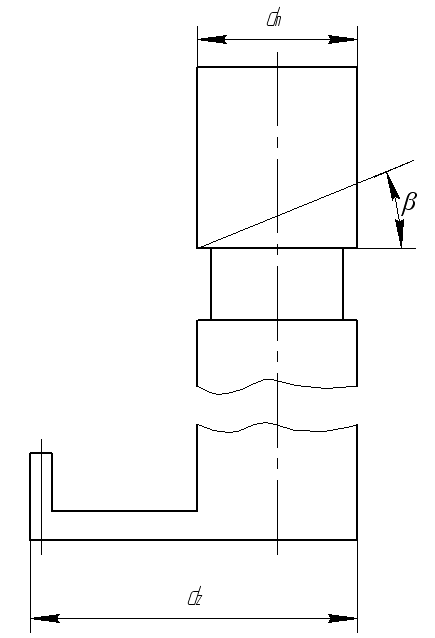
Рис. 2.1. Схема плунжера

Цикловая подача топлива

(2.9)

(2.10)

где , - часовой расход топлива на номинальном и режиме холостого хода, кг/ч;

- число цилиндров двигателя;

- плотность топлива, кг/л³;

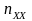- максимальные обороты холостого хода, мин^-1.

Часовой расход топлива на холостом ходу

(2.11)

где 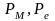- среднее давление механических потерь и среднее эффективное давление, МПа.

Максимальные обороты холостого хода

(2.12)

Координаты муфты регулятора на номинальном режиме

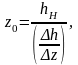(2.13)