
Аппроксимация функций. Решение слу методом Гаусса.
Задание: Для функции y=F(x), заданной таблично на отрезке [А, В] и заданной аппроксимирующей зависимости. Найти коэффициенты аппроксимирующей функции с использованием метода наименьших квадратов, Для нахождения значений коэффициентов решить систему линейных уравнений по методу Гаусса.
Таблица 2. Начальные данные.
8. |
f(x)=x / (ax+b) |
|
|
|
|
|
|
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
y |
56,9 |
67,3 |
86,6 |
200,9 |
240,5 |
474,1 |
490,6 |
518,5 |
Теоретическое введение:
Аппроксимация – нахождение аналитической (аппроксимирующей) зависимости, наиболее близкой к табличным данным. В качестве критерия близости чаще всего используют минимум суммы квадратов отклонений табличных значений от вычисленных по аналитической зависимости при одинаковых значениях входных параметров.
Метод наименьших квадратов – метод, заключающийся в нахождении коэффициентов функции подбором таких значений, чтобы, в конечном итоге, разность квадратов отклонений полученной функции и данной не превышала определенной величины ε.
Пусть надо решить систему уравнений:
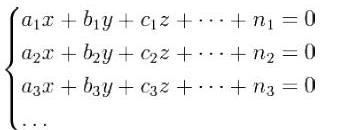
число которых более числа неизвестных x,y,z… Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных:
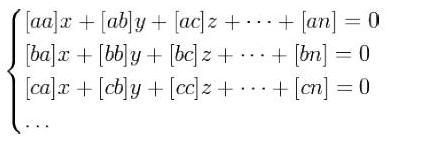
Из этой системы получаем систему нормальных уравнений:
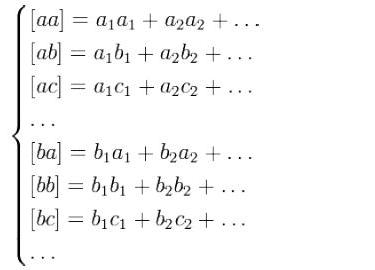
То есть, мы получим матрицу размером n*n и столбцом свободных коэффициентов. Которую можно решить методом Гаусса. Решение СЛАУ методом Гаусса наглядно разобрано и описано в проверке к задаче аппроксимации.
Текст программы:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace ConsoleApplication1
{
class Program
{
//Создаем метод вычисляющий параметры кривой аппроксимации и записывающий значения в матрицы х и у//
static void asd(double[] x, double[] y)
{
//Для решения системы линейных уравнений сводим систему уравнений к двум уравнениям по МНК//
double aa = 0, bb = 0, ab = 0, an = 0, bn = 0;
for (int i = 0; i < x.Length; i++)
{
aa = aa + x[i] * y[i] * x[i] * y[i];
bb = bb + y[i] * y[i];
ab = ab + x[i] * y[i] * y[i];
an = an + x[i] * x[i] * y[i];
bn = bn + y[i] * x[i];
}
an = -an;
bn = -bn;
double[] m = new double[] { aa, ab, an };
double[] mm = new double[] { ab, bb, bn };
//Решаем полученную матрицу методом Гаусса//
for (int i = 0; i < 3; i++)
{
m[i] = m[i] * ab - mm[i] * aa;
}
//Выражаем и находим сначала параметр x2, потом x1//
double x2 = m[2] / m[1];
double x1 = (mm[2] - mm[1] * x2) / mm[0];
x2 = -x2;
x1 = -x1;
Console.Write("Полученные параметры уравнения у=x/(ax+b): " + "a=" + "{0,7:f5}", x1); Console.WriteLine(" b=" + "{0,6:f4}", x2);
double sigma = 0,nev=0; int j = 0;
//Считаем значения среднеквадратичного отклонениния и невязки//
for (int i = 0; i < x.Length; i++)
{
sigma = sigma + (x1 * x[i] * y[i] + x2 * y[i] - x[i]) * (x1 * x[i] * y[i] + x2 * y[i] - x[i]);
nev = nev+(Math.Abs((x[i] / (x1 * x[i] + x2) - y[i]) / y[i]));
j = j + 1;
}
sigma = sigma / j;
nev = nev / j;
Console.WriteLine("Значение среднеквадратичного отклонения s="+"{0,6:f3}", sigma);
Console.WriteLine("Среднее значение невязки nev=" + "{0,6:f3}", nev);
}
static void Main(string[] args)
{
//Вводим данные для аппроксимации в массив l - значения х, в массив ll , соответственно, значения у//
double[] l = new double[] { 1, 2, 3, 4, 5, 6, 7, 8 };
double[] ll = new double[] { 56.9, 67.3, 86.6, 200.9, 240.5, 474.1, 490.6, 518.5 };
//Вызываем метод нахождения параметров СЛАУ присваивая х - значения массива l, а массиву у ,соответственно, значения массива ll//
asd(l, ll);
Console.ReadKey();
}
}
}
Результат:
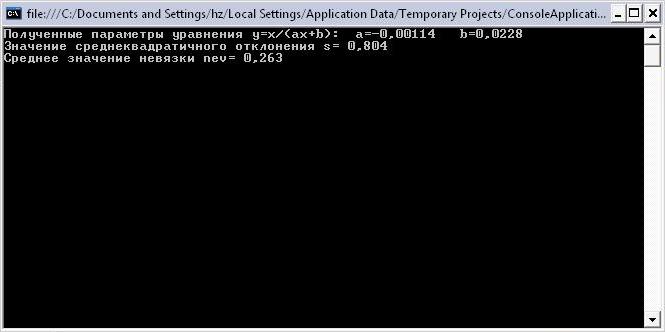
Вывод: Данная программа позволяет найти коэффициенты данной аппроксимирующей функции и вычислить невязку и среднеквадратичное отклонение аппроксимирующей функции.
