Н
ациональный
исследовательский технологический
университет
Московский институт стали и сплавов
Кафедра инженерной кибернетики
Курсовая работа по информатике
по теме:
«Применение программных средств для анализа и обработки данных»
Студент: Холодков Н.С.
Группа: Ф7-11-3
Вариант № 8
Преподаватель: Бесфамильный М. С.
Москва, 2013
Оглавление
Вычисление корней нелинейного уравнения методом итераций………………………стр.2
Вычисление определенного интеграла методом прямоугольников. …………………..стр.5
Интерполирование функции методом линейной интерполяции. ……………………...стр.8
Аппроксимация функций. Решение СЛУ методом Гаусса……………………………...стр.11
Вычисление корней нелинейного уравнения методом итераций.
Задание: Найти интервалы локализации корней и в каждом из интервалов найти корень
многочлена с заданной точностью методом Итераций.
Функция: F(x) = x4 + 3x3 – 55x2 – 99x + 632.5
Теоретическое введение:
Локализация корней – нахождение отрезков оси X, на которых функция имеет один корень.
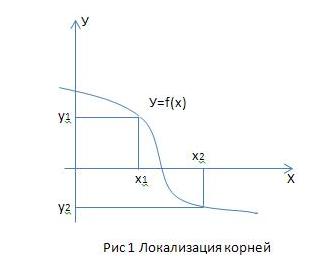
Для нахождения таких отрезков возьмем точки x1 и х2, то есть произвольный отрезок [х1; х2] (рис1). Проанализируем поведение функции на этом интервале, т.е. проверим меняет ли функция свой знак. Если меняет, то на данном интервале находится, как минимум, один корень.
Метод итераций (метод последовательных приближений) – последовательное приближение к корню уравнения путем уменьшения шага. На отрезке [х1; х2] имеется корень, возьмем 1/10 часть отрезка и начнем проверять условие смены знака, когда условие выполнится, уменьшим шаг еще на 1/10, пока значение корня не достигнет заданной точности.
Метод половинного деления заключается в следующем: разделим найденный отрезок [x1;x2] пополам и определим координату середины x=(x1+x2)/2. Если f(x)=0, то х является корнем уравнения, если f(x)<> 0, то выбираем тот из отрезков на концах которого функция имеет противоположные знаки. Если f(x1)*f(x)<0, то пересылаем значение x в значение x2, если наоборот, то пересылаем значение x в значение x1. Деление прекращается когда будет достигнута заданная точность.
Текст программы:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace ConsoleApplication1
{
class Program
{
delegate double fx(double i);
static double f1(double x)
{
return (x * x * x * x * x - 3 * x * x * x * x - 62 * x * x * x + 96 * x * x + 763 * x - 767.5);
}
static double asd(fx f, double h, double a, double b)
{
double k = 0, sl = 0, sp = 0, eps = 0.001;
Console.WriteLine("Интервалы локаизации корней:");
//Нахождение интервалов локализации корней с заданным шагом h//
while (a < b)
{
if (f(a) * f(a + h) < 0)
{
k = k + 1;
Console.Write("a=" + "{0,7:f3}", a);Console.Write( " b=" + "{0,7:f3}", (a + h));
Console.WriteLine();
//Нахождение корней методом половинного деления//
sl = a; sp = a + h;
double sm = 1;
while (Math.Abs(f(sm)) > eps)
{
sm = sl + (sp - sl) / 2;
if (f(sm) * f(sl) < 0)
sp = sm;
else sl = sm;
}
Console.WriteLine("Значение корня по методу половинного деления=" + "{0,7:f3}", sm);
//Нахождение корней методом Итераций с переменным шагом//
sl = a; sp = a + h;
while (Math.Abs(f(sl)) - Math.Abs(f(sp)) > 0.0001)
{
sp = sl + eps;
while (f(sl) * f(sp) > 0)
{
sl = sp;
sp = sp + eps;
}
eps = eps / 2;
}
Console.WriteLine("Значение корня по методу Итераций с переменным шагом=" + "{0,7:f3}", sl);
}
a = a + h;
}
return h;
}
static void Main(string[] args)
{
asd(f1, 0.1, -10, 10);
Console.ReadKey();
}
}
}
Результат:
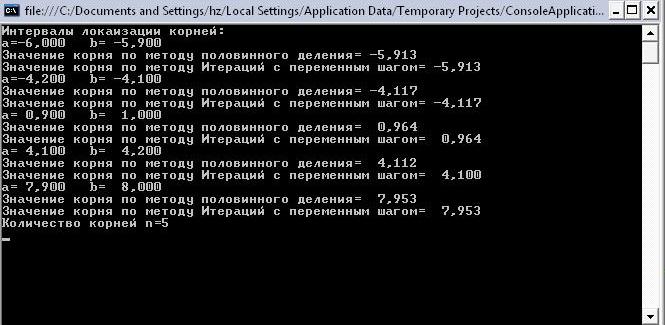
Вывод: Данная программа позволяет рассчитывать корни полиномов с точностью до тысячных (расхождения в результатах расчетов разными методами).