Конвективный теплообмен

При конвективном теплообмене теплота с поверхности металла уносится жидкостью или газом, которые перемещаются относительно поверхности.

Удельный конвективный поток

.

Определяется по правилу Ньютона, - коэффициент теплоотдачи.

.

Лучистый теплообмен

Любое нагретое тело излучает тепло. Излучение представляет собой электромагнитные колебания. Зависимость выражается уравнением Стефана-Больцмана:

- удельный тепловой поток радиации,

где - коэффициент зависит от состояния поверхности тела,

, - коэффициент черноты тела.

- для абсолютного черного тела.

- удельный тепловой поток радиации.

- коэффициент лучевого теплообмена или радиации.

Удельный тепловой поток полной теплоотдачи

,

,

.

Дифференциальное уравнение теплопроводности

Дифференциальное уравнение теплопроводности для пластины при наличии теплообмена с окружающей средой.

- коэффициент температуропроводности, ,

, - толщина пластины,

- коэффициент температуроотдачи, .

Дифференциальное уравнение стержня при наличии теплообмена с окружающей средой

,

,

- периметр стержня,

- площадь поперечного сечения стержня.

Диффузионное уравнение для трехмерного тела без теплообмена со средой

,

- оператор Лапласа.

Частный случай дифференциального уравнения

В условиях равновесия при длительном установившемся процессе каждый элемент получает столько тепла, сколько и отдает, т.е. , .

Краевые условия (граничные)

Чтобы рассчитать изменение температуры точек тела во времени, кроме закономерности распространения теплоты в теле необходимо знать еще два условия:

1. условия обмена тепла на границах рассматриваемого тела;

2. начальное распределение температуры по телу при времени t=0.

Условия могут быть разнообразны:

1. условие 1 рода или изотермическое условие; полагают, что поверхность тела обладает постоянной температурой в течение всего процесса распространения теплоты (сварка с интенсивным омыванием изделия водой);

2. условие 2 рода или адиабатическое – теплообмен на границах тела считаем равным нулю (сварка с изоляцией поверхности детали песком, асбестом);

3. условие 3 рода – условие теплообмена на границе тела со средой с заданной температурой; тепловой поток теплоотдачи по правилу Ньютона пропорционален разности температур изделия и среды

.

Но в то же время к границе притекает тепло согласно закона теплопроводности

,

.

Из условия 3 рода можем получить первые 2 условия.

Если теплоотдача очень велика, то приток тепла мал .

Если адиабатический.

Упрощенные схемы нагреваемого тела

а) Бесконечное тело. Имеет неограниченную протяженность по всем трем направлением .

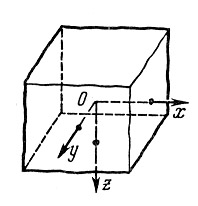
б) Полу бесконечное тело. Ограничено с одной стороны плоскостью , со стороны которой действует источник теплоты (наплавка валика на массивное тело).

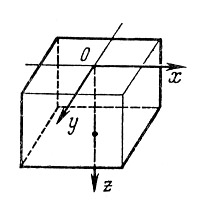
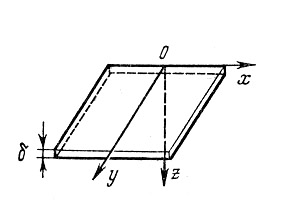
в) Бесконечная пластина ограничена параллельными плоскостями . Температура по толщине тела распространяется равномерно. Тепловой поток плоскостной (сварка со сквозным проплавлением).

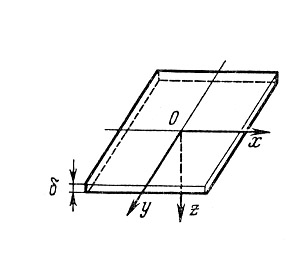
г) Полу бесконечная пластина ограничена и .

д) Плоский слой. Тело ограничено параллельными плоскостями . Тепловой поток искажен наличием ограниченных плоскостей, температура неравномерна.

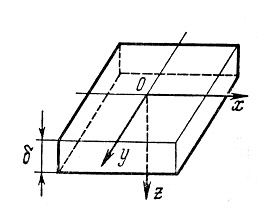
е) Бесконечный или полу бесконечный стержень. Температура в поперечном сечении стержня распределена равномерно. Тепловой поток линейный и распространяется вдоль оси х.