Labdevices( computer, “ibm pc”, 10) labdevices( computer, “vax-11”, 2)

Правило для селекции данных: selcomputers:-labdevices(computer, X, Y), write(“computer”, X, Y).

Выдаваемый результат отличается от строгого понятия кортежа, принятого в реляционных базах данных, так как здесь не преследуется цель проведения строгой математической аналогии между соответствующими понятиями баз данных и баз знаний.

Операция проекции отличается от операции селекция в том, что вывод выполняется не для всех компонентов строчек таблицы, а для некоторой их совокупности.

Если значения некоторых столбцов таблицы являются списками, то в теле правил селекции и проекции могут быть правила обработки списков. Например, в расписании поездов необходимо выбрать поезда, проходящие через некоторый город. Перечень промежуточных городов задан списком. В этом случае в тело правила поиска поездов необходимо ввести правило выявления наличия заданного города в списке промежуточных городов поезда. Аналогичным образом можно реализовать и другие реляционные операции. Для реализации операций объединения и пересечения в базу знаний следует вводить описания не менее двух таблиц.

14. Метод резолюций. Резольвенты. Полнота метода. Отличие от классических схем вывода. Понятие о дизъюнктах. Демонстрация метода на примере дерева вывода.

Непосредственная реализация механизмов формального вывода в логических программах с большими базами знаний сопряжена с большим перебором вариантов, что может существенно замедлить процесс решения задачи. Поэтому логическое программирование требует поиска специфичных процедур вывода. Наиболее популярным в логических программах в настоящее время считается метод резолюций, предложенный Дж. Робинсоном. В его основе используется способ доказательства от противного. В этом случае вместо выводимого утверждения берётся его отрицание и рассматривается совместно с исходными истинными утверждениями. Если показывается, что полученная система противоречива, то это означает, что доказуемое утверждение истинно. Дж. Робинсоном была предложена эффективная процедура реализации этого подхода. Основную идею метода можно пояснить, используя понятие интерпретаций формул: пусть некоторая формула W логически следует из некоторого множества истинных формул S (SW). Это означает, что для всех интерпретаций, для которых истины все формулы S, истина формула W. Если некоторая интерпретация удовлетворяет S и W, то она не удовлетворяет S и W. Таким образом, можно сделать вывод, что если из SW, то S и W – противоречиво. Вместо доказательства SW можно доказывать противоречие S и W. Для доказательства противоречивости S и W Рубенсон предложил процедуру “Принцип резолюции”. Для использования правила резолюции необходимы формулы определённого вида. Эти формулы называются дизъюнкторами. Не должны содержать ,,,.

ab=(ab)(ba)(ab,ba).

Формулы должны быть дизъюнкциями литералов.

Рубенсон доказал, что принцип резолюций полон и непротиворечив. Непротиворечивость: если в результате применения принципа резолюций получено пустое предложение, то исходное множество предложений невыполнимо.

Правило резолюции: пусть D₁ и D₂ - дизъюнкты, P – логическая переменная, либо литерал, причём в D₁ есть P, а в D₂ есть P. Пусть дизъюнкт (D₁ – P) – это дизъюнкт, в котором из D₁ удалён P, аналогично (D₂ – P). D=(D₁ – P)(D₂ – P) – резольвента дизъюнктов D₁, D₂. Это означает, что дизъюнкт D выводится из дизъюнктов D₁ и D₂.

Резольвентный вывод из множества дизъюнктов S есть конечная последовательность дизъюнктов, каждый из которых либо из S, либо получен из представления дизъюнктов по правилам резолюций.

Рубинсон показал, что если множество формул S и W противоречиво, то многократное применение правил резолюций приведет к пустому множеству, то есть если из S и W получено Nil, то W логически следует из S. Правило резолюций позволяет всегда получить Nil из исходного множества истинных дизъюнктов формул противоречиво.

Теорема: непустое множество дизъюнктов S невыполнимо тогда и только тогда, когда из S выводится пустой дизъюнкт (S[]).

Принцип резолюции применим как к формулам логики предикатов, так и к формулам высказываний.

Пример: принцип резолюции в логики высказываний.

1)SP; 2)US; 3)U; 4)WR; 5)W; 6)PQ; 7)PR;

Доказать: |-P(QR)=PQPR (PQPR)=(PQ)(PR)

8)Пр(1,6)=SQ; 9)Пр(2,3)=S; 10)Пр(7,1)=SR; 11)Пр(10,9)=R; 12)Пр(4,11)=W;

1 3)Пр(5,12)=NIL.

Пример: ab; bc. Доказать ac.

1)ab; 2)bc; |- ac; ac

3)a; 4)c

16. Построение опровергающих деревьев в логике высказываний. Доказательство непротиворечивости множества дизъюнктов. Замкнутые деревья.

Пусть задано S=S(p₁,…,p_n) – множество дизъюнктов, где p_i – логические переменные.

С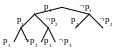 емантическое дерево Т для S – конечное бинарное дерево, в i-том ярусе которого помечено 2 ребра p_i и p_i. Каждая ветвь дерева задаёт некоторую интерпретацию.

Семантическое дерево отражает все 2ⁿ интерпретаций. Узел N в семантическом дереве Т для S называется опровергающим, если путь в Т от корня до N задаёт такие истинностные значения переменных p_i, в которых опровергается некоторый дизъюнкт D из S и никакой другой узел этим свойством не обладает. Множество дизъюнктов S – невыполнимо тогда и только тогда, когда любая ветвь в семантическом дереве Т для S имеет опровергающий узел. Если обрезать семантическое дерево Т для S, удалив из Т все поддеревья с корнями в опровергающих узлах, оставив сами опровергающие узлы в Т, то полученное дерево называется замкнутым семантическим деревом для S. Множество дизъюнктов S невыполнимо тогда и только тогда, когда в замкнутом семантическом дереве все его концевые узлы – опровергающие.

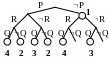
Пример: {P;PQ;QR;QR}

1. P - 1; 2) (PQ)= PQ - 2;

2. (QR)= QR - 3; 4) (QR)=QR - 4.

18. Понятие о логической программе. Структура логической программы. Факты, правила, целевые утверждения. Алгоритм доказательства цели.

Логическая программа состоит из набора хорновских предложений и целевых утверждений. Хорновские предложения называют дизъюнктами, клозами, процедурами. Хорновские дизъюнкты представляют собой логические формулы BA₁,…,A_n, где А_i, В_i, – литералы, атомарные функции. Литерал можно представить: R(t₁,…,t_m), m>0, R – линейное отношение, t_i – аргументы.

Термы - константы, переменные, выражения вида f(t_i1,…,t_jk) – k-арная функция.

(A₁,…,A_n)BBA₁…A_n.

Переменные действуют только в одном предложении. Одно и то же имя в разных предложениях указывает разные объекты.

Выделяют 3 вида предложений: факт, правило (условное утверждение), цель.

Логическая программа рассматривает факты и правила как аксиомы. Они составляют базу знаний. Правило, в котором используется переменные называются универсальными.

Правила – это суждения, которые из известных фактов выводит новое утверждение.

Цели Q₁,Q₂.

AB₁,…,B_n,D₁,D₂

AT₁,T₂

Целевое утверждение (предложение):

Q(x)=Q₁,Q₂,..,Q_k

D₁,D₂,..,D_m,Q

 Nil, то

D₁,D₂,..,D_m,Q

Удовлетворение цели означает доказательство одновременной истинности всех подцелей на основе базы знаний программы Q=Q₁Q₂…Q_k. Цель истинна, когда все её подцели могут быть формально выведены с помощью метода резолюций или с помощью modus ponens.

Цель Е выводится из базы знаний (p₁,…,p_n), если из множества хорновских дизъюнктов (p₁,…,p_n,Е) выводится пустой дизъюнкт.

По отношению к логическому программированию высказывания А и АВ следует понимать как утверждения базы знаний, а В - это задача, которую необходимо решить пользователю. Ее решение (истинность) следует из данной базы знаний. Пользователь получает ответ “да” или значения аргументов задачи В, при которых В истинна.

Непосредственная реализация механизмов формального вывода в логических программах с большими базами знаний сопряжена с большим перебором вариантов, что может существенно замедлить процесс решения задачи. Поэтому логическое программирование требует поиска специфичных процедур вывода. Наиболее популярным в логических программах в настоящее время считается метод резолюций, предложенный Дж. Робинсоном. В его основе используется способ доказательства от противного. В этом случае вместо выводимого утверждения берётся его отрицание и рассматривается совместно с исходными истинными утверждениями. Если показывается, что полученная система противоречива, то это означает, что доказуемое утверждение истинно.