35 Лема Неймана –Пірсона.

Нехай і - задані постіними, і -рішаюча функція така що

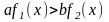
, якщо

якщо

У випадку якщо в якості можна взяти будь-яке значення. або .

Тоді для будь-якої рішаючої функції

Доведення. Якщо - інша рішаюча функція, то нехай і підмножини виморочного простору 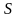, і визначаються наступним чином:

Тоді

Оскільки будь-яка рішаюча функція задається указанням множини , на якій вона приймає значення , то знаходження рішаючої функції мінімізуючої лінійну комбінацію , рівносильно визначенню множини , для якої останній інтеграл приймає найменше значення. Цей інтеграл досягає мінімуму , коли множина включає всі точки , для яких інтегральна функціє набуває відємного знаку, і не включає тих точок в яких підінтегральна функція додатня. При цьому не грає ролч чи входять точки рівні 0. Рішаючи функція , визначена за допомогою множини задовільняю умови 2 і 3.

36. Опуклі функції. Нерівність Єнсена

О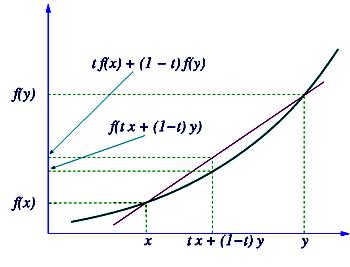 пукла функція — функція, яка визначена на опуклій множині лінійного простору, і задоволняє нерівності

при всіх λ [0, 1].

Нехай область визначення опуклої функції f(x) лежить в скінченовимірному просторі, тоді f(x) неперервна в будь якій внутрішній точці цієї області.

Нехай x₁, ..., x_m — будь які точки із області визначення опуклої функції f(x), λ₁, ..., λ_m — невід'ємні числа, які в сумі дорівнюють 1. Тоді

Якщо f(x) — двічи неперервно диференційована опукла функція, то матриця її других похідних напівдодатньо визначена.

Нерівність Йєсена

Нехай функція опукла вниз. Тоді для будь-якої випадкової величини ξ зі скінченним першим моментом

Лема

Нехай функція опукла. Тоді для будь-якого у знайдеться число с(у) таке що при всіх х .

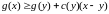Доведення

Візьмемо в умовах леми . Тоді .Обчислимо математичне сподівання обох частин нерівності. Оскільки, і нерівність між математичними сподіваннями зберігається із наслідку (1), тоді

Наслідок (1):

Наслідок математичного сподівання:

• Якщо ξ ≤ η, тоді Mξ ≤ Mη

• Якщо ξ ≤ η, і при цьому Mξ = Mη тоді ξ ≤ η

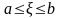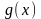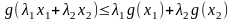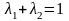
Нерівність Йeнсена , - опукла, , , , має місце нерівність .

Д оведення: Оскільки , 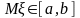. Проведемо дотичну в точці до функції : .

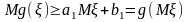
Кінець доведення.

Якщо функція сильно опукла , то знак заміняють на .

Якщо функція опукла вгору, то знак заміняють на протилежний.

Наслідок Нехай 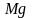- середній прибуток( - прибуток), якщо 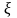- інтерпритувати як виграш гравця в деякій грі і функція корисності гравця опукла(сильно опукла), тоді згідно нерівності Йенсена 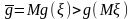і нехай маємо гру, в якій , то ця нерівність доводить, що гравець, у якого функція корисності опукла буде грати. А для гравця, у якого функція корисності опукла вгору, маємо і він грати не буде.

37,

38,

39,Системи Підтримки прийняття рішень класифікація сппр

Категорії класифікації	Ознака (основа) класифікації	Класифікаційні групи (типи систем)
Концептуальна модель	Інформаційний підхід	Концептуальна модель Спрага Модель еволюціонуючої СППР
	Підхід, оснований на знаннях	Орієнтовані на знання СППР Орієнтовані на правила СППР
	Інструментальний підхід	Спеціалізовані (прикладні) СППР СППР-генератори СППР-інструментарії
Користувачі	Ієрархічний рівень управління	Вища ланка управління (виконавчі інформаційні системи) Середня ланка управління Нижча ланка управління
	Спосіб взаємодії користувача з системою	Термінальний режим Режим клерка Режим посередника Автоматизований режим
	Ступінь залежності осіб у процесі прийняття рішення	Персональна підтримка (персональ­ні СППР) Групова підтримка (групові СППР) Організаційна підтримка (багатокористувацькі, інтерорганізаційні, інтраорганізаційні СППР)
Завдання, що по­требує прийняття рішень	Новизна завдання	Унікальні проблеми (СППР на даний випадок) Повторювані проблеми (інституціальні СППР)
	Характер описання проблеми	Цілісний вибір Багатокритеріальний вибір (наприклад, СППР Decision Grid)
	Тип моделі	Об'єктивна модель Суб'єктивна модель
	Діапазон підтримува­них функцій	Функціонально-специфічні СППР СППР загального призначення
Забезпечуючі за­соби	Рівень підтримки прийняття рішень	СППР, орієнтовані на дані СППР, орієнтовані на моделі СППР, орієнтовані на документи СППР, орієнтовані на комунікації Web-орієнтовані СППР
	Рівень мов користувацького інтерфейсу	Процедурні мови Командні мови Непроцедурні мови Природні мови
Галузі застосу­вання	Професійна сфера	Мікроекономіка Макроекономіка Конторська діяльність (офісні СППР) Оцінювання розповсюдження тех­нологій Юриспруденція Медицина і т.д..
	Часовий горизонт	Стратегічне управління (довгостро­кові рішення) Тактичне управління (середньостро-кові рішення) Операційне управління (коротко­строкові рішення)

40

41

42

43

44

45

46

47 Динамічне програмування дозволяє розв’язувати поставлену задачу на основі об’єднання розв’язків знайдених для допоміжних задач.

При цьому варто зазначити, що термін програмування в даному контексті базується на основі табличного методу, а не написанні комп’ютерної програми. Крім того, якщо в методові розбиття задача ділиться на декілька незалежних між собою задач, кожна з яких вирішується рекурсивно, після чого із розв’язків проміжних задач і формується розв’язок початкової задачі, то динамічне ж програмування, навпаки, застосовується тільки тоді, коли проміжні задачі не є незалежними, тобто різні допоміжні задачі використовують розв’язки одних і тих же підзадач, причому в алгоритмі динамічного програмування кожна проміжна задача вирішується тільки один раз, після чого відповідь зберігається в таблиці. Останнє дає можливість уникати одних і тих же обрахувань кожного разу, коли працюємо з даною підзадачею.

Динамічне програмування, як правило, використовується для задач оптимізації, для яких можлива наявність багатьох рішень. Кожному варіанту розв’язку можна співставити деяке значення і нам потрібно знайти серед них той, який є оптимальним (мінімальним або максимальним). Такий розв’язок називають одним із можливих оптимальних розв’язків. Враховуючи те, що таких розв’язків може бути декілька, їх варто розрізняти від єдиного оптимального рішення.

Процес розробки алгоритмів динамічного програмування можна розбити на 4 нижченаведені етапи:

1. Опис структури оптимального розв’язку.

2. Рекурсивне визначення значення, що відповідає оптимальному розв’язку.

3. Обчислення значення, що відповідає оптимальному рішенню за допомогою методу висхідного аналізу.

4. Отримання оптимального розв’язку на основі інформації, отриманої на попередніх кроках.

Етапи 1-3 складають основу методу динамічного програмування. Етап 4 можна пропустити, якщо треба дізнатись тільки значення, що відповідає оптимальному. На 4 кроці інколи використовується додаткова інформація, отримана із попереднього, щоб полегшити процес побудови оптимального рішення.

49 Принцип оптимальності Белмана

Теорія рішень

Динамічне програмування – собливий метод оптимізації, який використовується при багатокрокових операціях.

Нехай О* - деяка операція, яка розбивається на m послідовних кроків.

Нехай W – міра ефективності цієї операції, припустимо, що вона складається з суми ефективностей на кожному кроці:

Позначимо X=(x₁,x₂,…x_m) – (х_i відповідає і-ому кроку) послідовність дій яка впливає на виграш(ефективність) в цілому і на виграш на кожному кроці або просто керування. Задача зводиться до пошуку такого Х^* при якому W=> max, його будемо називати оптимальним управлінням, а виграш на ньому:

W=max{W(x)}

З першого погляду здається, що дію на кожному кроці треба обирати за принципом максимального виграшу на поточному кроці – А хрін там! Управління повинно обиратись з врахуванням його наслідків у майбутньому – на інших кроках.

Тобто управління на і-ому кроці повинне обиратися таким чином, щоб максимальною була сума виграшів на усіх кроках, що залишились включаючи поточний – Це і є принцип оптимальності Белмана.