
- •Система прийняття рішень. Загальна задача прийняття рішення.
- •2. 3,4, Параментричні і непараметричні Ср. Лотерейна та Матрична ср. Приклади
- •Непараметричні ситуації прийняття рішень. Приклади.
- •5,6 Перетворення мсср у лсср. Перетворення лсср у мсрр. Еквівалентність
- •6.Перехід від лотерейної до матричної ситуації прийняття рішень та повернення до тієї ж лспр.
- •5.Перехід від матричної моделі до лотерейної
- •11, 12. Перетворення ммср і лмср при стохастичній закономірності
- •13. Функція корисності
- •18. Функція втрат. Невід’ємна функція витрат
- •17. Очікувана корисність. Теорема Наймана-Моргенштерна
- •19. Критерій Вальда
- •20. Критерій Севіджа
- •21. Критерій Гуровіця
- •22. Критерій Лапласа
- •25. Баєсівський ризик та баєсівське рішення
- •Байєсівський ризик
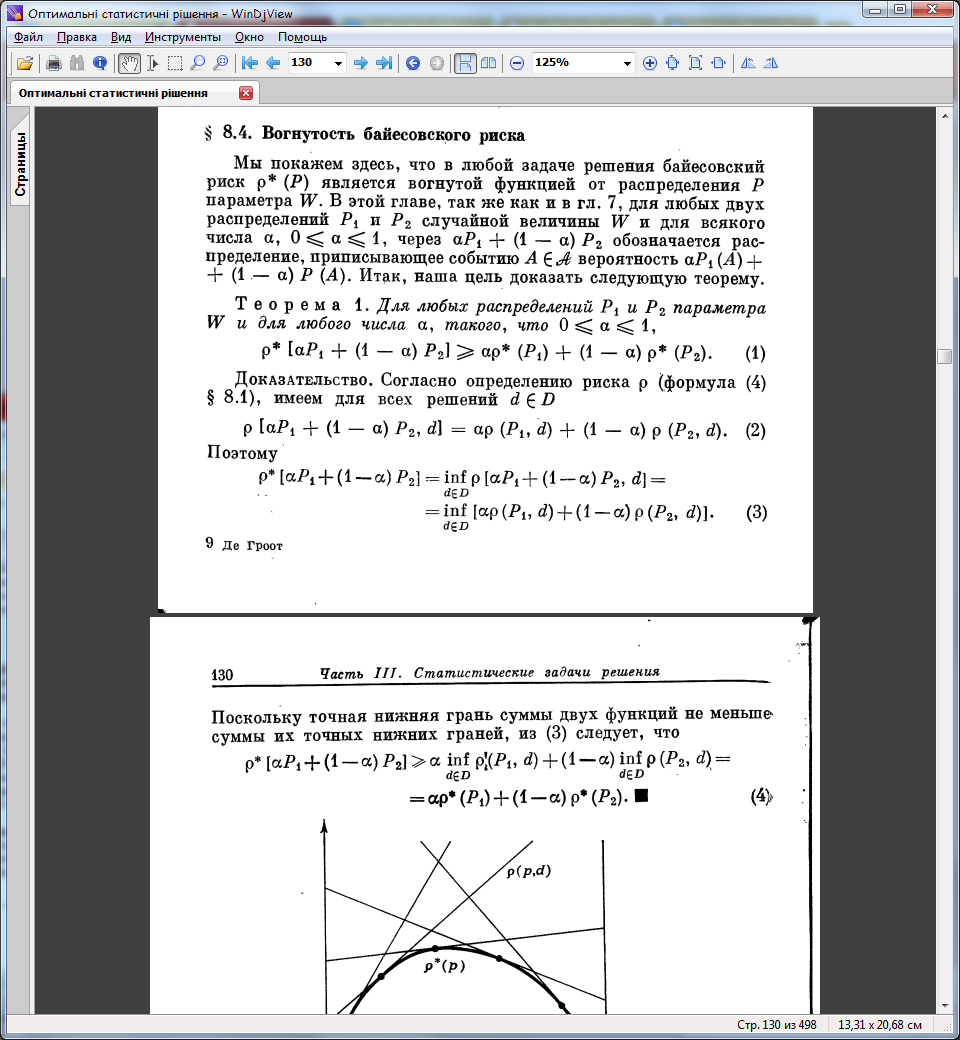
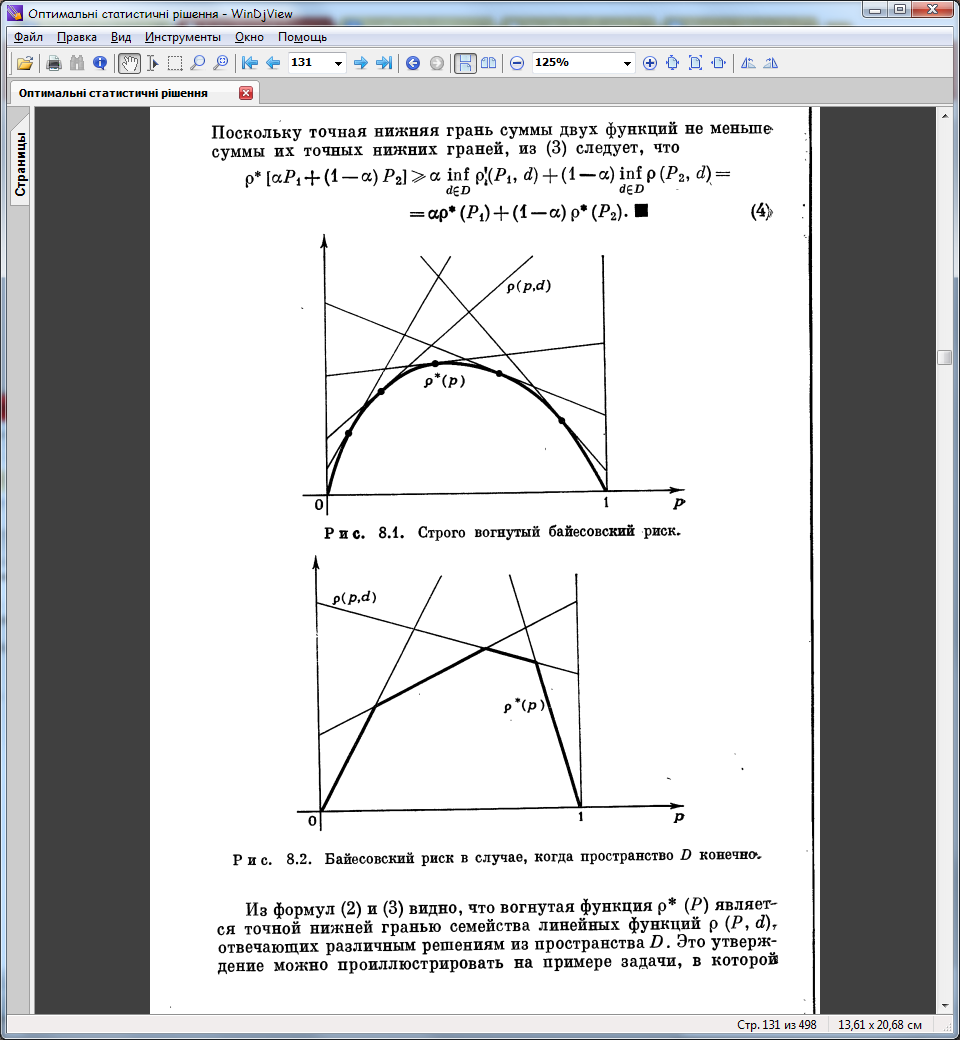
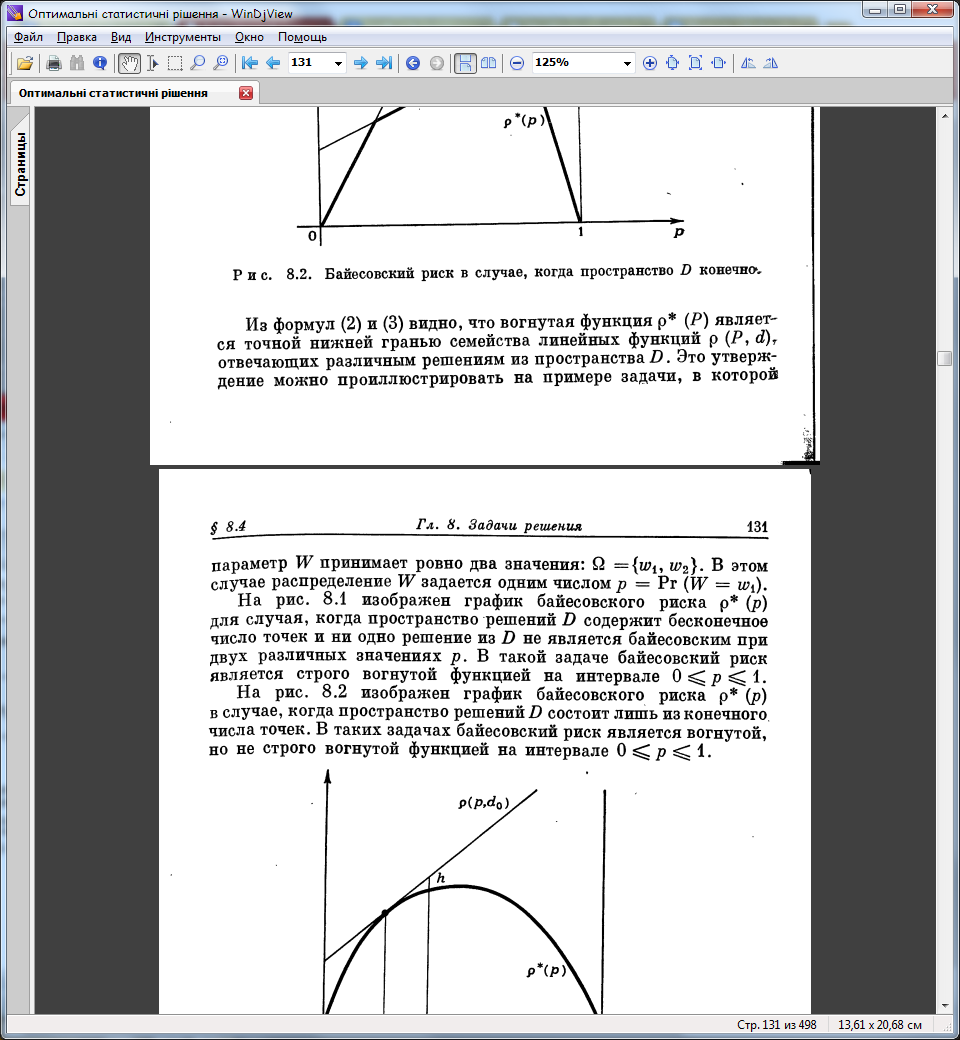
- •26. Увігнутість баєсівського рішення
- •27,Рандомізація у теорії ігор та теорії рішень.
- •35 Лема Неймана –Пірсона.
- •36. Опуклі функції. Нерівність Єнсена
- •39,Системи Підтримки прийняття рішень класифікація сппр
22. Критерій Лапласа
Критерій Бернуллі-Лапласа використовують у випадку, коли можна припусти, що будь-який з варіантів середовища не більш ймовірний, ніж інший. Тут передбачається, що всі стани середовища (всі варіанти реальної ситуації) рівноймовірні.

Для кожної стратегії Аі (і -го варіанта рішення) слід розрахувати середній очікуваний доход (математичне очікування) за формулою (3.25), і відповідно до критерію Бернуллі-Лапласа слід вибирати варіант (стратегію Аi ), для якого досягається найбільше значення:
![]()
23.
24.
25. Баєсівський ризик та баєсівське рішення

Байєсівський ризик
Розглядаючи задачу рішення з простором параметрів Ω, простором рішень D і функцією втрат L.
Для певного розподілу Р параметру W, баєсівський ризик ρ*(P) – це точна нижня грань ризиків ρ (P,d) по всіх ризиках d.
ρ*(P)=infd є D ( ρ(P,d) ).
Кожне рішення, ризик якого рівний баєсівському ризику називається баєсівським рішенням при розподілі Р. тобто, ρ(P,d*) = ρ*(P) => d* -- баєсівське.
Виявляється, можлива ситуація, коли немає баєсівського рішення – таке можливо тільки тоді, коли нижня грань за формулою баєсівської границі не досягається ні при одному d є D.
Тоді, вибирається баєсівське рішення, яке «достатньо мало» відрізняється від баєсівського.
26. Увігнутість баєсівського рішення
27,Рандомізація у теорії ігор та теорії рішень.
В задачах рішення часто буває дійсним припущення, що рішення d є D вибирається за допомогою додаткової процедури, наприклад, підкидаючи монету. Тобто, приймається змішане рішення – спочатку рішенням приписуються ймовірності, а тоді, згідно з цими ймовірностями, вибирається одна з них.
В таких випадках, втрати цього рішення, згідно з припущенням про середню корисність будуть вираховуватися так: L(w,d)=SUM_i=1INF [pi * L(w,di)]. (1)
Якщо простір подій незліченний, то рандомізовані рішення можна позначати більш загально – якийсь розподіл на сігма-алгебрі, підмножин множини D.
Рандомізовані рішення позначаються М. тоді зрозуміло, що чисті рішення входять в рандомізовані (D є M): вистачає поставити ймовірності при всіх рішеннях 0, крім того, яке ми хочемо подати. (якщо є D={d1,d2,d3}, то рішення m є M подається як (m=α*d1+β*d2+(1- α- β)*d3). m, відповідне чистому рішенню d1: m=1*d1+0*d2+0*d3.)
Стосовно рандомізованих рішень важливим є твердження, що рандомізовані рішення не можуть зменшити мінімальний ризик, який було знайдено на чистих рішеннях.
Згідно з формулою (1), ризик рандомізованого рішення – це середньозважений ризик, розрахований з функцій втрат чистих рішень. З цього випливає, що, якщо існує ризик ρ(P,d) змішаного рішення, то його значення дорівнює суміші ризиків ρ(P,di) чистих рішень di.
З чого випливає, що
InfdєM [ρ(P,d)] = inf dєD [ρ(P,d)] =ρ*(P).
Тобто якщо є відрізок, то мініум його лежить на кінцях, і ніяк не можу бути на середині. Тобто, фактично, рандомізовані рішення задають всі можливі комбінації чистих рішень (з 2-х рішень роблять відрізок, з більше – якусь фігуру, а ця площина, що утворюється (гіперплощина у вищих просторах) не може виходити за межі твірних точок, якими і є чисті рішення.
28.
29.
30.
31
32. Побудова байєсівських вирішуючих функцій нормальним методом.

Апріорний розподіл - розподіл на Ω, який відомо до експерименту.
Апостеріорний розподіл - умовний розподіл на Ω за умови, що ми спостерігали .
Апостеріорний розподіл дає нам додаткову інформацію про параметр і може зменшити байєсівський ризик.
Формула Байєса для обчислення апостеріорного розподілу

ξω(X)=
-ймовірність настання параметра ω, якщо спостерігали .
33. Побудова байєсівських вирішуючих функції екстенсивним методом
Нехай маємо умову:
Задача:
знайти, при якому розподілі величини ω1 та ω2 рішення d1 (ω2) , буде байєсівським d*.
Розв"язок:
визначимо розподіли ω1 та ω2:
P(ω1) = ξ P(ω2) = 1-ξ
1)
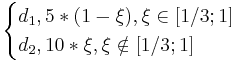
значення експериментів y1, y2 спостереження випадкової величини w1, w2:

