17. Очікувана корисність. Теорема Наймана-Моргенштерна

Аксиоматика:

19. Критерій Вальда

Критерій Вальда є критерієм крайнього песимізму, оскільки статистик вважає, що "природа" діє проти нього найгіршим чином. Це критерій гарантованого результату.

Нехай гру задано матрицею виграшів гравця А. Тоді на думку статистика - гравця А, дії гравця "природа", якій діє проти нього найгіршим чином, відображуються в реалізації гравцем "природа" таких своїх стані Пj , при яких величина виграшу гравця А (статистика) приймає найменше значення minaij. Виходячи з цього статистик обирає таку чисту стратегію Аi , при якій найменший виграш minaij буде максимальним, тобто забезпечувати максимін: '

Велична аβ , що розраховується за формулою (3.12), називається нижньою ціною гри - це максимальний виграш, що є гарантованим в грі з певним противником шляхом вибору однієї зі своїх стратегій при мінімальних результатах.

Нехай гру задано матрицею програшів гравця А, тоді найгірші дії гравця "природа", будуть реалізовуватися в таких станах Пj , при яких величина програшу гравця А (статистика) приймає найбільше значення maxaij. Виходячи з цього статистику необхідно обрати таку чисту стратегію Аi , при якій найбільший програш maxaij буде мінімальним, тобто забезпечувати мінімакс: '

Критерій Вальда забезпечує максимізацію мінімального виграшу або, що теж саме, мінімізацію максимального програшу (втрат), який може виникнути при реалізації однієї зі стратегій. Цей критерій орієнтує ОПР дотримуватися вкрай обережної поведінки. Така поведінка прийнятна наприклад, коли гравець не має зацікавленості в крупному виграші, але хоче себе застрахувати від неочікуваних програшів. Вибір такої поведінки визначається відношенням гравця до ризику. Критерій Вальда застосовують у тих випадках, коли необхідно забезпечити успіх в будь-якій ситуації.

20. Критерій Севіджа

Виникають ситуації, в яких неконтрольовані фактори діють більш приємним чином у порівнянні з найкращім становищем, на яке орієнтувалась ОПР. Наприклад, погодні умови оказалися краще прогнозованих; конкуренція зменшилась на ринку у порівнянні з прогнозованими очікуваннями. У цих умовах виникає необхідність визначення можливих відхилень отриманих результатів від їх оптимальних значень. У цьому випадку застосовують критерій Севіджа.

Цей критерій аналогічний попередньому критерію Вальда, але ОПР використовує не матрицю виграшів А, а матрицю ризиків Я .

За критерієм Севіджа кращим є рішення, при якому максимальне значення ризику буде найменшим, тобто

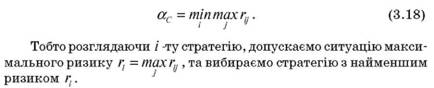
Для застосування критерію Севіджа до ситуації пред'являються ті ж самі умови, що й для критерію Вальда.

21. Критерій Гуровіця

Критерій песимізму-оптимізму Гурвіца

Цей критерій рекомендує в процесі прийняття рішення використовувати певний середній результат, що характеризує стан між крайнім песимізмом і крайнім оптимізмом.

У випадку, коли гру задано матрицею виграшів за критерієм Гурвіца перевага віддається варіанту рішення, яке визначається максимумом серед лінійних комбінацій мінімального і максимального виграшів:

Коефіцієнт λ можна розглядати як показник оптимізму.

При λ = 0 критерій Гурвіца співпадає з максимаксним критерієм, тобто орієнтація на граничний ризик, оскільки великий виграш спрягається з великим ризиком. При λ = 1 критерій Гур-віца співпадає з критерієм Вальда, тобто орієнтація на обережну поведінку. Тому критерій Гурвіца це називають критерієм узагальненого максиміну.

Значення λ є проміжними між ризиком і обережністью і вибирається із суб'єктивних (інтуїтивних) міркувань в залежності від конкретних умов та схильності до ризику ОПР.

У випадку, коли гру задано матрицею програшів за критерієм Гурвіца перевага віддається варіанту рішення, яке визначається мінімумом серед лінійних комбінацій мінімального і максимального виграшів:

Формулу (3.20) застосовують також у випадку, коли задано матрицю ризиків.

Критерій Гурвіца застосовується у випадку, коли:

про ймовірність появи стану Пj нічого не відомо;

з появою стану Пj необхідно вважатися; реалізується тільки мала кількість рішень; допускається деякий ризик.