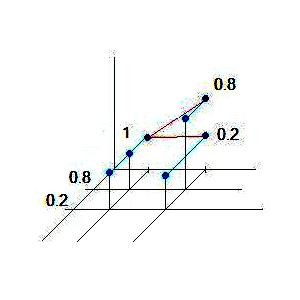
5.Перехід від матричної моделі до лотерейної

Необхідно перетворити матричну модель в лотерейну, тобто яка складається з лотерейної схеми та інформації .Треба побудувати відображення , яке буде задовольняти умові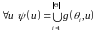

Маємо:

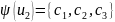
Тепер треба перенести інформацію. При дії наслідок наступає при будь-якому значенні параметра , для якого . Тому розумно встановити між розподілами і таку залежність

Оскільки ми вважаємо, що є тільки одне істинне значення параметра , то події 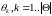є несумісними, а отже для будь якої їх суми справедливо

Тому

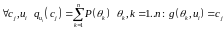
Таким чином:

0,6

Дискретні розподіли:

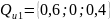
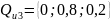
7. Невизначеність у СПР

Невизначеність у ЛСПР існує, якщо:

- Дві різні дії призводять до таких самих двох різних наслідків

- Якщо одна дія призводить до двох деяких наслідків, а інша до хоча б одного наслідку, відмінного від попередніх.

Це справедливо, якщо ми не фіксуємо Відношення Переваг на Наслідках для ТПР.

В разі, якщо існує порядок на наслідках, необхідною і достатньою умовою невизначеності буде:

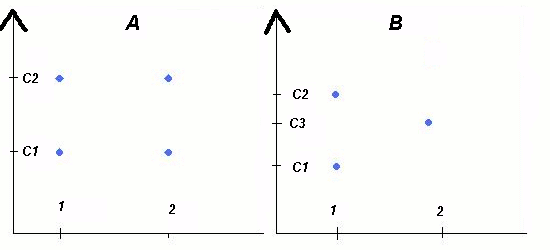
• За означенням невизначенності: "Коли два ТПР, з однаковими відношеннями переваг оберуть дві різні дії"

• У варіанті B Перший ТПР обере дію 1, бо може отримати максимальний виграш - С2, а Другий ТПР обере дію 2, бо не схильний до ризику і надає перевагу гарантованому виграшу С3

• У варіанті А, на перший погляд, дві дії еквівалентні, оскільки мають однакові наслідки. АЛЕ: завжди будуть ТПР1 та ТПР2, для яких виграш(1)>виграш(2) та виграш(1)<виграш(2) відповідно. І той та інший буде мати рацію.

Алгоритм Перевірки на невизначенність:

1)шукаємо дію (for по всіх таких діях), в якої>1 наслідку.

2) якшо 2 наслідки: шукаємо іншу дію (<> наша знайдена).

2а) якшо в неї є два наслідки, які такі ж як і наші два насліки, то ситуація невизначена.

2б) якшо в неї є наслідок, якого немає серед наших наслідків, то ситуація невизначена.

3) якшо >2 наслідків:

3а) шукаємо іншу дію (не наш знайдений) в якго є ХОЧ ОДИН наслідок. якшо знаходимо -- є невизначеність.

11, 12. Перетворення ммср і лмср при стохастичній закономірності

Побудувати модель МСПР по заданій моделі (зі стохастичною закономірністю) ЛСПР

Перевести МОДЕЛЬ=перевести СХЕМУ+перевести ІНФОРМАЦІЮ. Схему переводимо аналогічно до Матрична ситуація прийняття рішень. Розподіл на W будуємо так: для кожного параметру ймовірність його появи визначатимемо, як добуток ймовірностей настання відповідних наслідків за кожної дії P(ω)=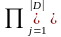 P_dj(g(ω,d_j))

Побудувати модель ЛСПР по заданій моделі (зі стохастичною закономірністю) МСПР

Z_М Z_Л - так як і в Лотерейна ситуація прийняття рішень

I_М I_Л: P_dj(c_i)= P(ω_k)

d_j D, c_i C, j 1..|D|, i=1..|C|