1. Аналитическое решение задачи перевозки неоднородного груза

Задача:

1-й склад (А1) имеет сталь двух марок: 3000т. марки «а» и 4000т. марки «б». 2-й склад (А2) имеет сталь марки «а» - 5000т. и марки «б» - 2000т. Сталь должна быть вывезена в два пункта потребления : в пункт В1 необходимо поставить 2000т. стали марки «а», 3000т. - марки «б» и остальные 2000т. стали любой марки.

Аналогично, второй пункт потребления В2 должен получить 8250т. стали, из них 1000т. марки «а» и 1500т. марки «б».

Известно, что 2т. стали марки «а» могут заменить 1,6тю марки «б».

Стоимость перевозок в рублях за тонну составляют: из А1 в В1 и В2 1руб. и 1,5руб. соответственно и из А2 в В1 и В2 2руб. м 1 руб.

Составить оптимальный план.

Решение:

Прежде всего, необходимо вычислить коэффициент взаимозаменяемости:

Исходя из этого коэффициента пересчитаем все данные:

Потреб. ресурсы		В1			В2
		2000	2400	1600	1000	1200	4600
А1	3000	1	1	1	1,5	1,5	1,5
	3200	1,25	1,25	1,25	1,875	1,875	1,875
А2	5000	2	2	2	1	1	1
	1600	2,5	2,5	2,5	1,25	1,25	1,25

Кроме того, выполняются условия:

3000+3200+5000+1600 = 2000+2400+1600+1000+1200+4600;

3000+5000 > 2000+1000;

3200+1600 > 2400+1200.

Следовательно, задача разрешима.

В связи с тем, что в 1-м и 3-м столбцах указаны потребности только на груз Ic., они не могут быть удовлетворены из ресурсов А₁₂=3200 и А₂₂=1600 груза IIс. Поэтому клетки (2,1), (2,3), (4,1) и (4,3) блокируются с помощью произвольно больших затрат М. Аналогично блокируются клетки, через которые ресурсы Iс. не могут удовлетворить потребности в грузе IIс., т.е. клетки (1,2), (1,4), (3,2) и (3,4).

После всех преобразований получим таблицу:

Потреб. ресурсы		В1			В2
		2000	2400	1600	1000	1200	4600
А11	3000	1	М	1	1,5	М	1,5
А12	3200	М	1,25	1,25	М	1,875	1,875
А21	5000	2	М	2	1	М	1
А22	1600	М	2,5	2,5	М	1,25	1,25

После всех выполненных операций данную задачу можно решать как обычную транспортную задачу, рассматривая условно четырех поставщиком и шести потребителей.

Составление опорного плана:

Потреб. ресурсы		В1			В2
		2000	2400	1600	1000	1200	4600
А11	3000	1 2000	М	1 1000	1,5	М	1,5
А12	3200	М	1,25 2400	1,25 600	М	1,875 200	1,875
А21	5000	2	М	2	1 1000	М	1 4000
А22	1600	М	2,5	2,5	М	1,25 1000	1,25 600

После составления получаем: количество заполненных ячеек m+n-1 (где m –количество строк, а n – количество столбцов) 4+6-1. Минимальные затраты на этом шаге равны:

1*2000 + 1,25*2400 + 1*1000 + 1,25*600 + 1*1000 + 1,875*200 + 1,25*1000 + 1*4000 + 1,25*600 =14125

Оценка критерий оптимальности решения:

Добавим дополнительную строку и столбец

Потреб. ресурсы		В1			В2
		2000	2400	1600	1000	1200	4600
А11	3000	1 2000	М	1 1000	1,5	М	1,5	-1
А12	3200	М	1,25 2400	1,25 600	М	1,875 200	1,875	-1,25
А21	5000	2	М	2	1 1000	М	1 4000	-1
А22	1600	М	2,5	2,5	М	1,25 1000	1,25 600	-1,25
		0	0	0	0	-0,625	0

Потреб. ресурсы		В1			В2
		2000	2400	1600	1000	1200	4600
А11	3000	0 2000	М-1	0 1000	0,5	М	0,5	-1
А12	3200	М-1,25	0 2400	0 600	М-1,25	0 200	0	-1,25
А21	5000	1	М-1	1	0 1000	М-1,625	0 4000	-1
А22	1600	М-1,25	1,25	1,25	М-1,25	-0,625 1000	0 600	-1,25
		0	0	0	0	-0,625	0

После ввода всех значений пересчитаем результат и произведем цикл пересчета поставок:

⁰ ₂₀₀

⁰

0

200

^-1.625 ₁₀₀₀

⁰ ₆₀₀

1200

400

Пересчитав поставки получаем оптимальное решение:

Потреб. ресурсы		В1			В2
		2000	2400	1600	1000	1200	4600
А11	3000	0 2000	М	0 1000	0,5	М	0,5
А12	3200	М	0 2400	0 600	М	0,625	0 200
А21	5000	1	М	1	0 1000	М	0 4000
А22	1600	М	1,25	1,25	М	0 1200	0 400

Пересчитав элементы 2-го и 3-го, 5-го и 6-го столбцов в этом решении путем деления их на α=0,8, получим окончательное оптимальное решение, выраженное уже не в условных, а в реальных единицах:

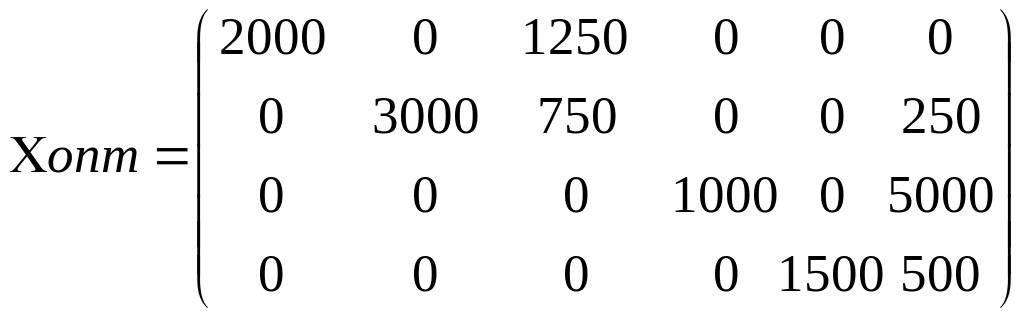и Z=15 375 руб.