4. Уравнение Бернулли.

Определение. Уравнением Бернулли называется дифференциальное уравнение первого порядка, которое может быть записано в виде

.

Можно предложить следующий метод решения этого уравнения. Неизвестную функцию y(x) будем искать в виде , где - неизвестная функция, а - некоторая функция, выбранная специальным образом. (Способ выбора будет описан позже). Производная равна: . Подставляя и в исходное уравнение, получаем:

+ .

Полученное уравнение преобразуем к виду

.

Подберем функцию из условия: .

(Это уравнение для определения функции является уравнением с разделяющимися переменными и нас интересует не его общее решение, а какое либо частное решение не равное тождественно нулю).

Тогда для определения имеем уравнение

.

Это уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными и способ его решения изложен ранее.

Пример. Найти решение задачи Коши:

, .

Вначале найдем общее решение этого уравнения. Будем искать в виде . Тогда, подставляя и в исходное уравнение, получим: . Функцию определяем из условия: ; ; ; ; . Определим : ; ; +С; ; 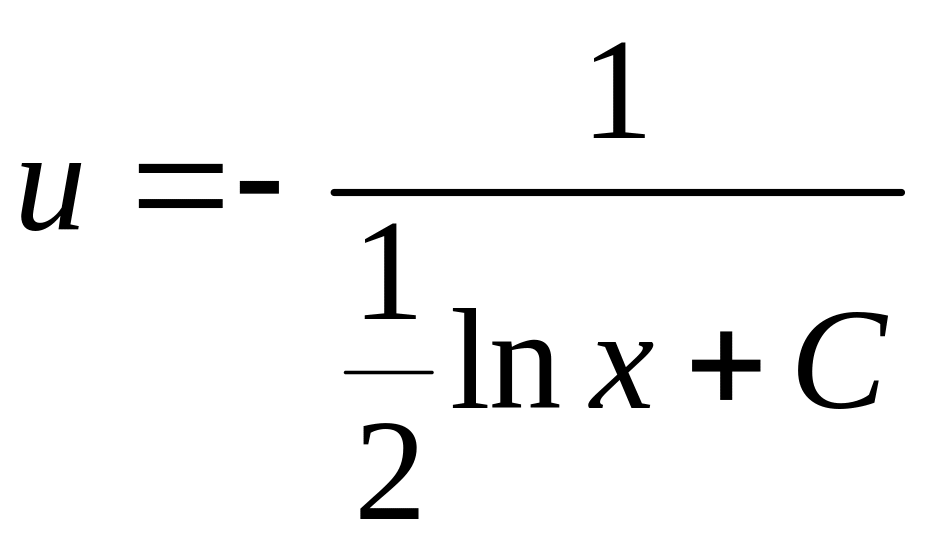. Следовательно, общее решение имеет вид . Из условия определяем произвольную постоянную С: ; .

Ответ: .

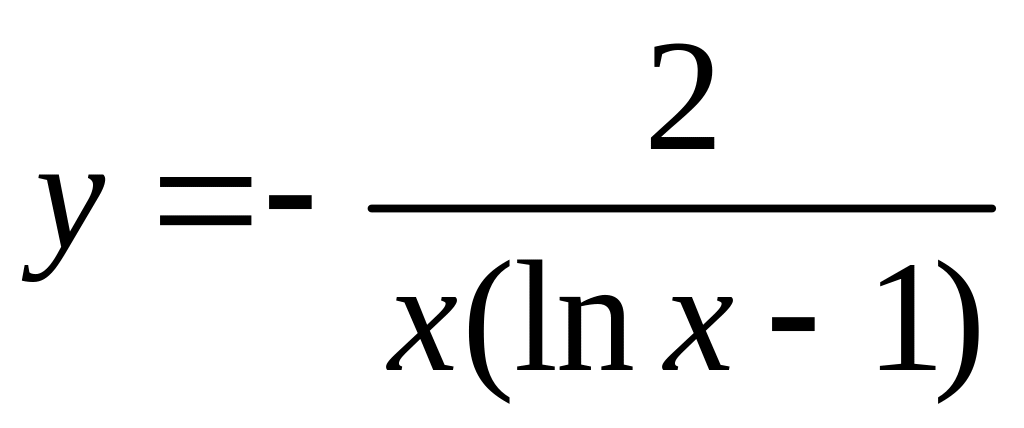Пример. Найти решение задачи Коши:

, .

Данное уравнение является уравнением Бернулли. Будем искать в виде . Тогда, подставляя и в исходное уравнение, получим: . Функцию определяем из условия: ; ; ; ; . Определим : ; ; +С; ; 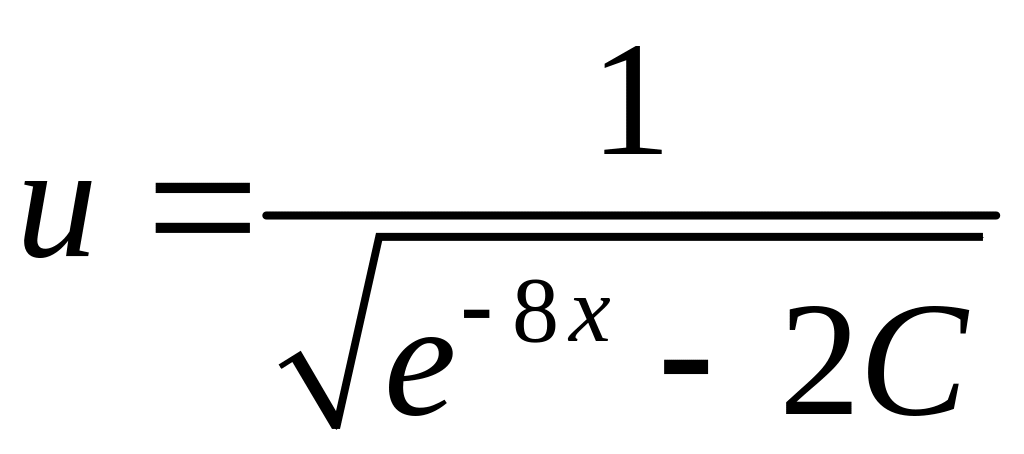.( Знак плюс при извлечении квадратного корня выбран исходя из начальных условий). Следовательно, общее решение имеет вид . Из условия определяем произвольную постоянную С: ;

Ответ: .

Пример. Найти решение задачи Коши:

, .

Вначале найдем общее решение этого уравнения. Будем искать в виде . Тогда . Подставляя и в исходное уравнение, получаем:

; .

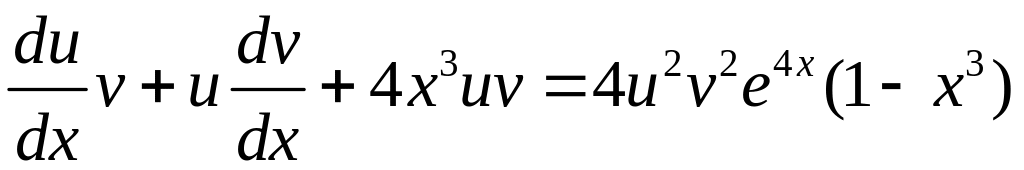Функцию определяем из условия: , 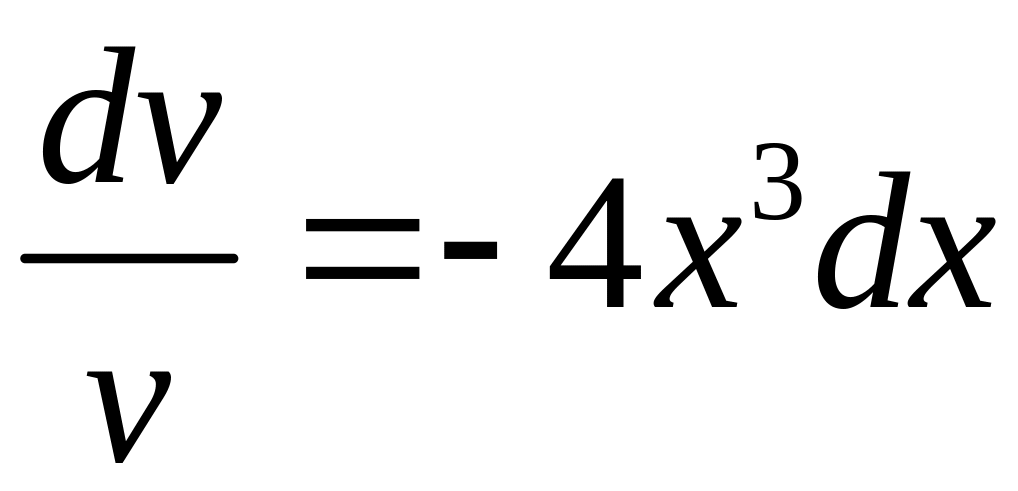; ; 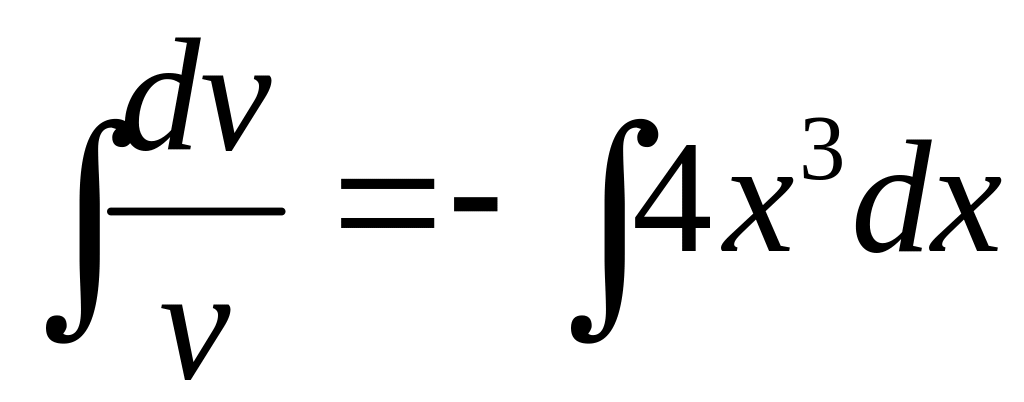; . Определим :

; ; .

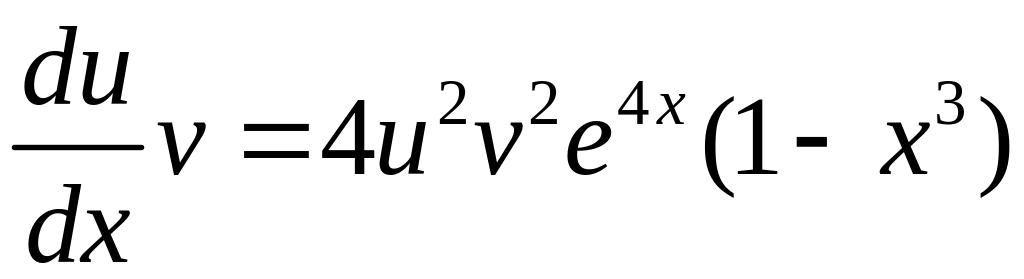Интегрируем правую и левую части полученного соотношения

.

Приведем схему вычисления полученных интегралов.

.

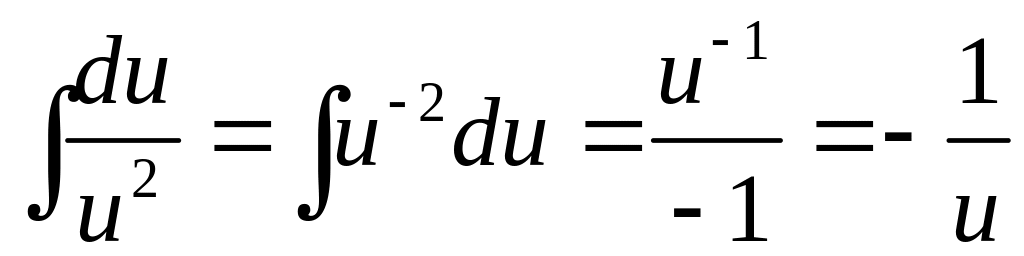Для вычисления сделаем замену переменных , , . Тогда получаем

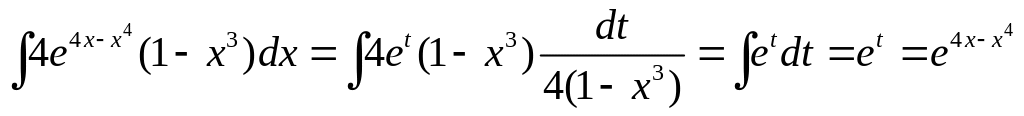
Подставляя полученные интегралы в исходное выражение, получаем , . Следовательно , общее решение имеет вид .

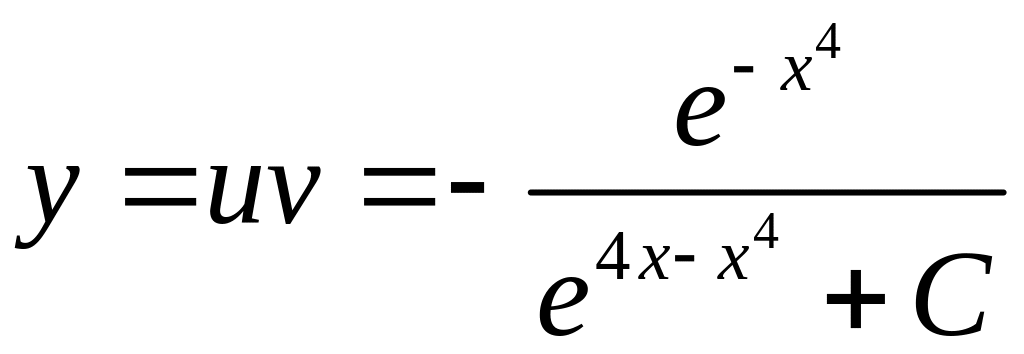Используя начальные условия задачи Коши, определим С.

Так как , то 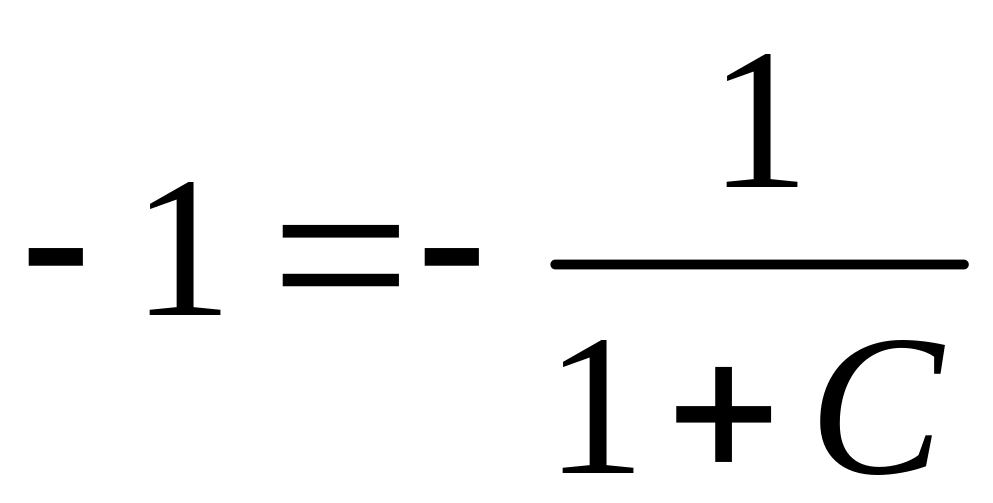, С=0.

Тогда имеем .

Ответ: .

Типы рассмотренных уравнений и методы их решения сведены в таблицу 1. Приведем решение еще одного уравнения с использованием указанной таблицы.

Пример. Решить уравнение

1.Переменные не разделяются, так как .

2.Подставим в и , получим . Из скобки невозможно вынести , т.е. функция не является однородной. Вывод: это не однородное уравнение.

3.Выделим линейную часть вида . Делим уравнение на , и учитываем, что . Тогда:

; , но . Линейная часть относительно и не выделяется. В таком виде это уравнение не может быть отнесено ни к типу линейных уравнений, ни к типу уравнений Бернулли.

4.Поменяем ролями функцию и аргумент. Разделим уравнение на и учтем, что 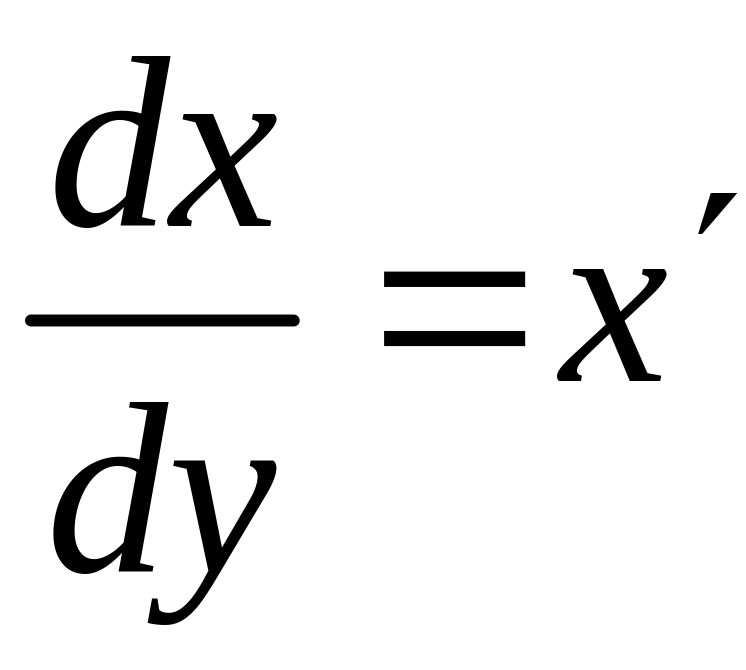. Тогда: 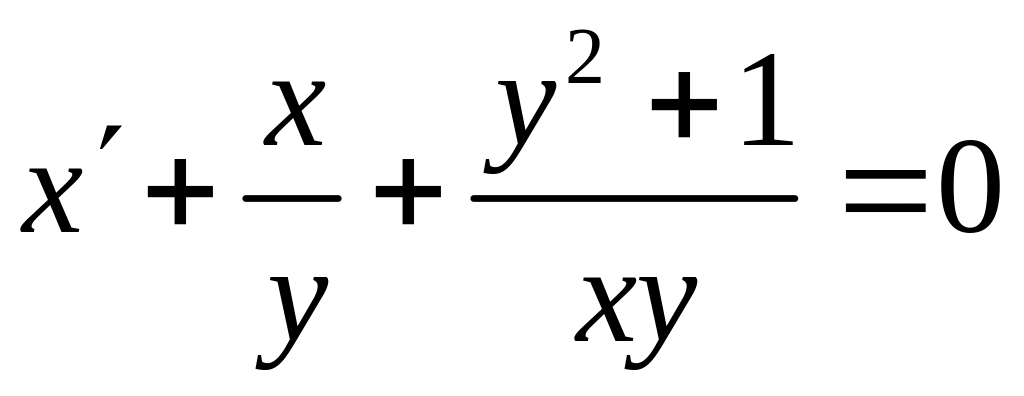. В этом дифференциальном уравнении легко просматривается линейная относительно и часть: 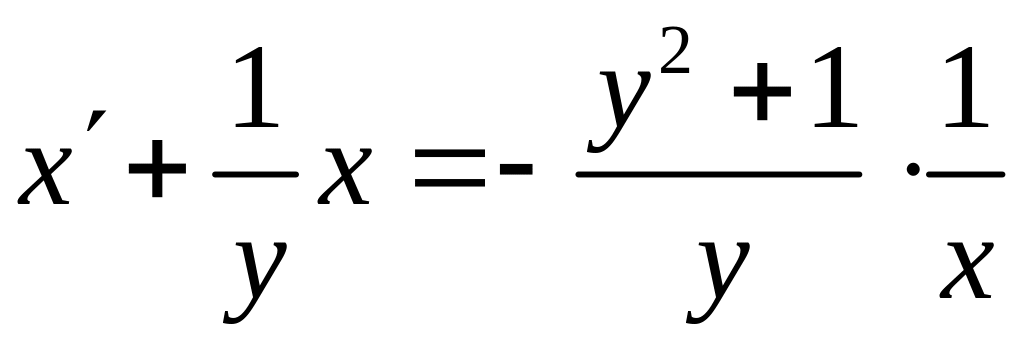. В правой части этого соотношения видим в степени и делаем вывод, что это уравнение относится к типу уравнений Бернулли относительно . Решаем его с помощью подстановки . Тогда: ; .

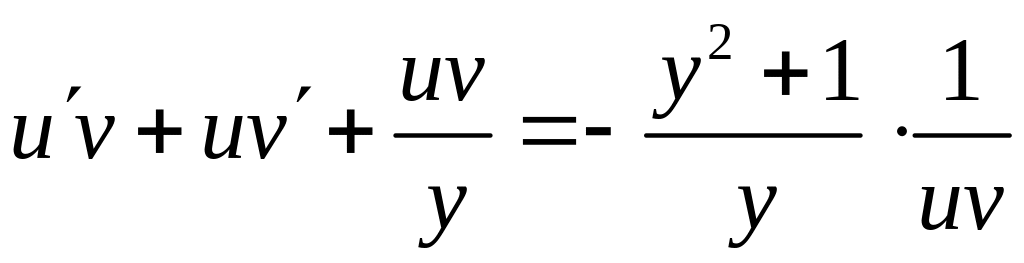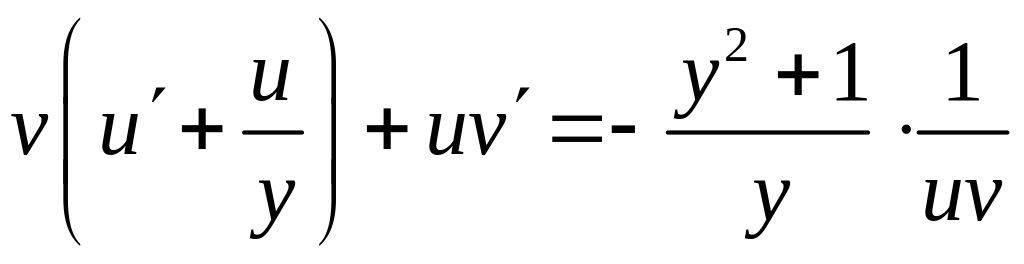Пусть ; ; ; ; .

; ; ; ;

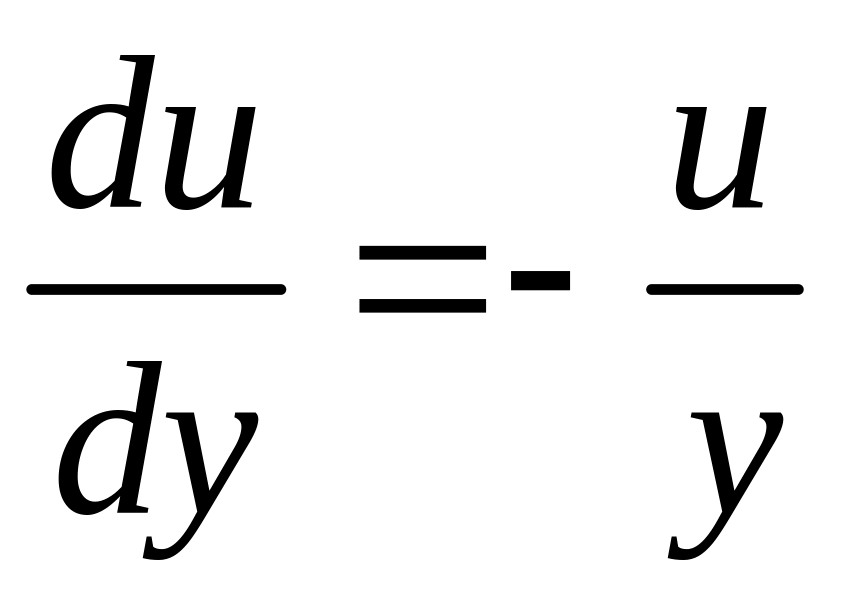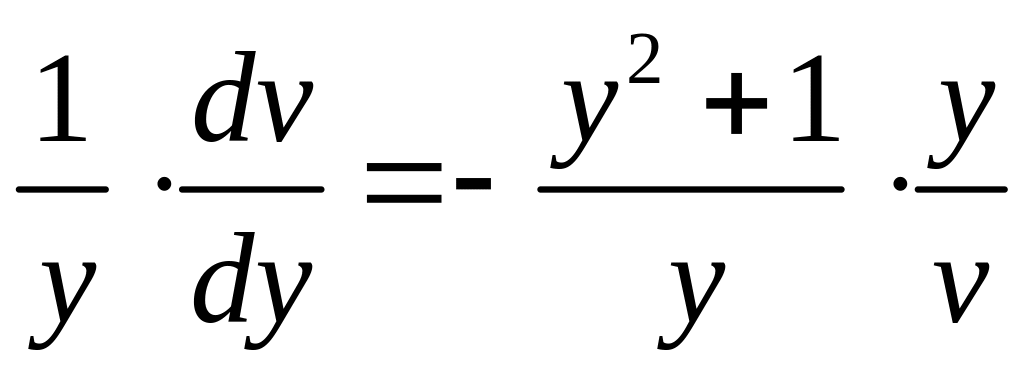. Ответ удобно искать в виде: ; .

Ответ: .

	Тип уравнения	Вид уравнения		Способ решения
1.	Уравнения с разделяющимися переменными	Можно привести к виду	Можно привести к виду	Учитывая, что , преобразовать уравнение к виду и интегрировать обе части
2.	Однородные уравнения	Можно привести к виду	и должны быть однородными функциями одного измерения:	Подстановка приведет уравнение к уравнению с разделяющимися переменными. При этом или
3.	Линейные уравнения	Приводятся к виду или		а) Подстановка (или ) б) Метод вариации постоянной
4.	Уравнения Бернулли	Приводятся к виду ,

Таблица 1.