15

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Московский государственный университет приборостроения и информатики

Кафедра высшей математики дифференциальные уравнения

(решение задач)

Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.

Москва 2005

Излагаются основные методы решения обыкновенных дифференциальных уравнений. Пособие является частью пособия для заочного отделения (автор Антонова И.И., МГУПИ), содержащей уравнения с разделяющимися переменными, однородные уравнения, линейные уравнения первого порядка, уравнения Бернулли, некоторые уравнения высших порядков.

Часть 1. Дифференциальные уравнения первого прядка.

Прежде чем перейти к решению конкретных типов задач, напомним некоторые общие положения, касающиеся дифференциальных уравнений первого порядка.

Дифференциальным уравнением первого порядка, разрешенным относительно производной, называется соотношение вида

.

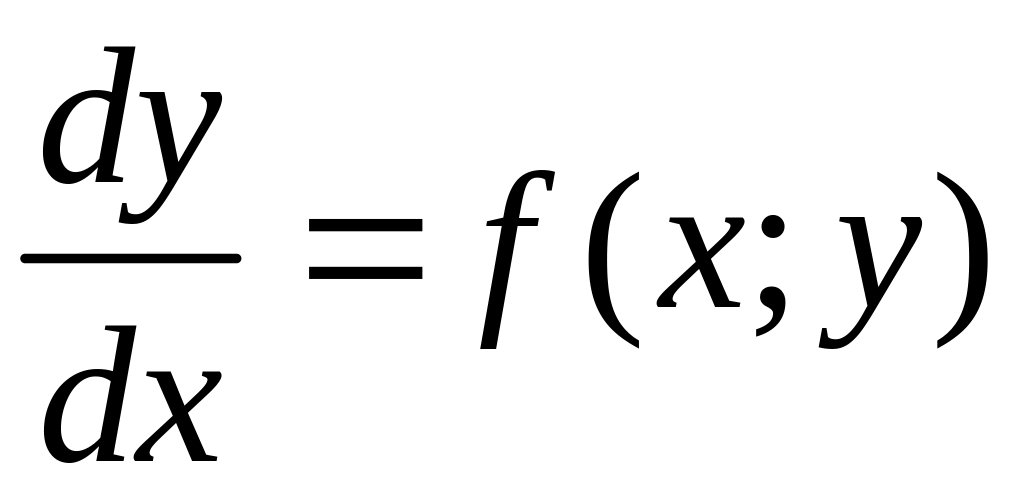Частным решением дифференциального уравнения называется любая функция , при подстановке которой в дифференциальное уравнение, оно превращается в тождество.

Задачей Коши для дифференциального уравнения первого порядка называется задача отыскания решения дифференциального уравнения

,

удовлетворяющего условиям, при .

Известно, что если в некоторой области функция непрерывна вместе со своей частной производной , то в этой области задача Коши имеет решение и при том единственное.

Общим решением дифференциального уравнения первого порядка в некоторой области называется совокупность функций (С – произвольная постоянная), удовлетворяющая двум условиям:

1.При любом значении произвольной постоянной С функция является частным решением дифференциального уравнения;

2. Для любых начальных условий задачи Коши при найдется значение произвольной постоянной , такое что .

Если общее решение неявно определятся соотношением вида , то такое соотношение называется общим интегралом дифференциального уравнения первого порядка. Далее рассмотрим методы решения тех классов дифференциальных уравнений первого порядка, которые представлены в контрольной работе.

1.Уравнения с разделяющимися переменными.

Определение. Уравнением с разделяющимися переменными называется уравнение, которое может быть записано в виде:

.

Можно предложить следующую схему решения этого уравнения. Разделяем переменные, то есть уравнение переписываем в виде:

.

Интегрируя левую и правую части этого уравнения, получаем:

,

где С – произвольная постоянная.

Полученное соотношение является общим интегралом исходного дифференциального уравнения.

Замечание. Если функция равна нулю в точках , то функции , ,…., являются решениями исходного уравнения. При изложенном методе такие решения могут быть потеряны, поэтому их рекомендуется выписать отдельно.

Пример. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде (x,y)=C).

.

Для того, что бы убедиться, что данное уравнение действительно является уравнением с разделяющимися переменными, выразим . Имеем

Тогда , 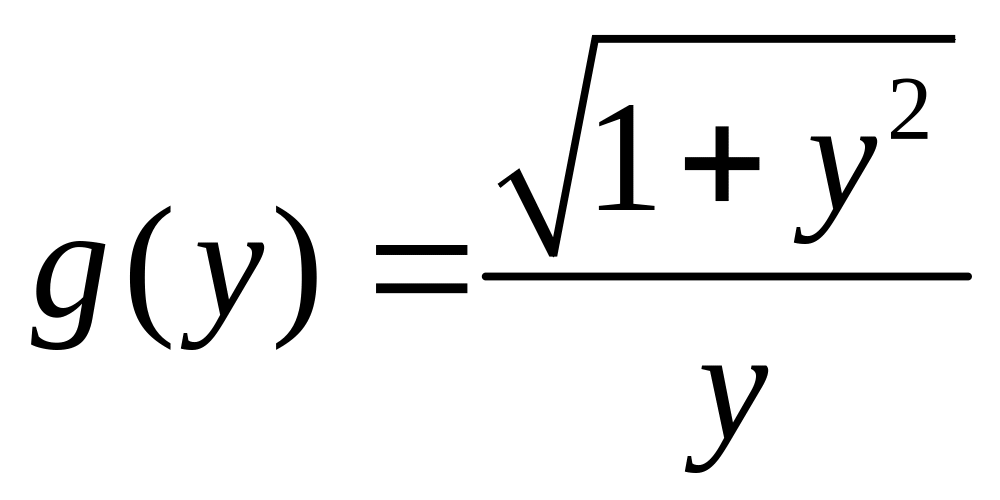. Заметим, что . Разделяем переменные:

.

Интегрируя правую и левую части, получаем

.

Приведем схему вычисления интеграла: = .

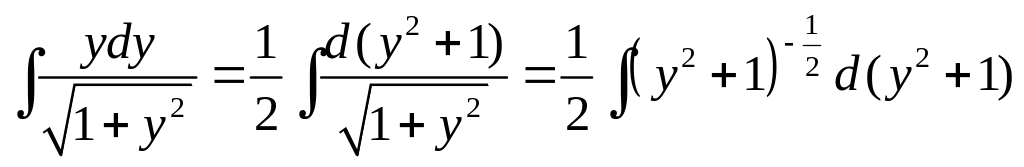После вычисления интегралов имеем: .

Ответ: .

Пример. Найти общий интеграл дифференциального уравнения.

.

Уравнение запишем в виде

.

Тогда 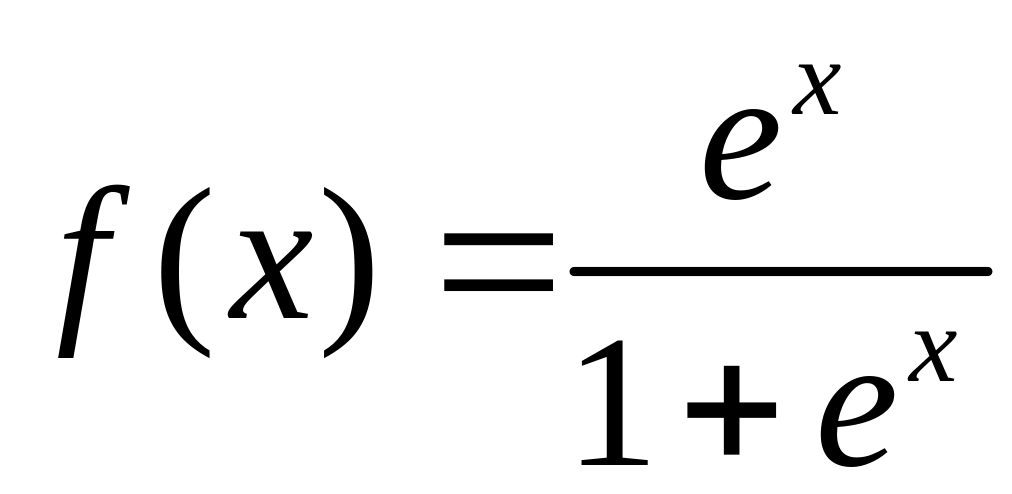, . Заметим, что при . Следовательно, функция является решением данного дифференциального уравнения.

В случае разделяем переменные:

.

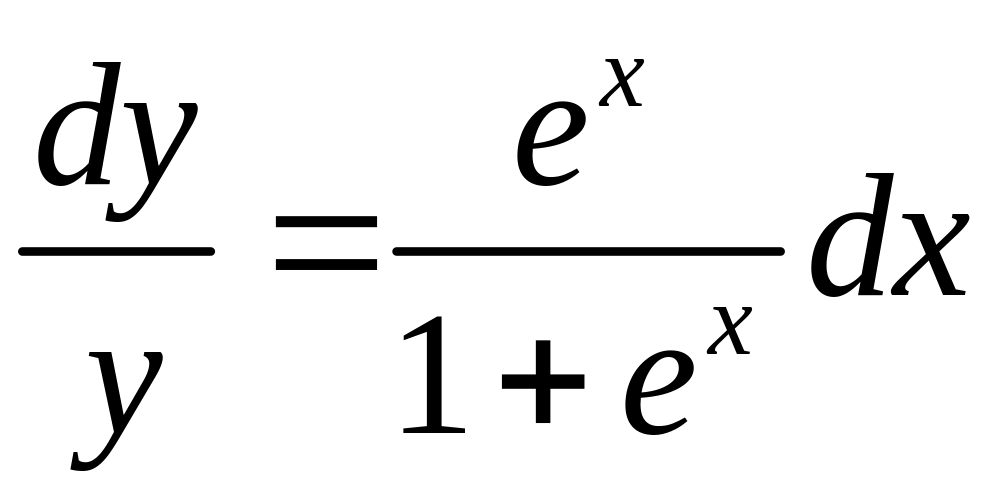Интегрируя правую и левую части, получаем

.

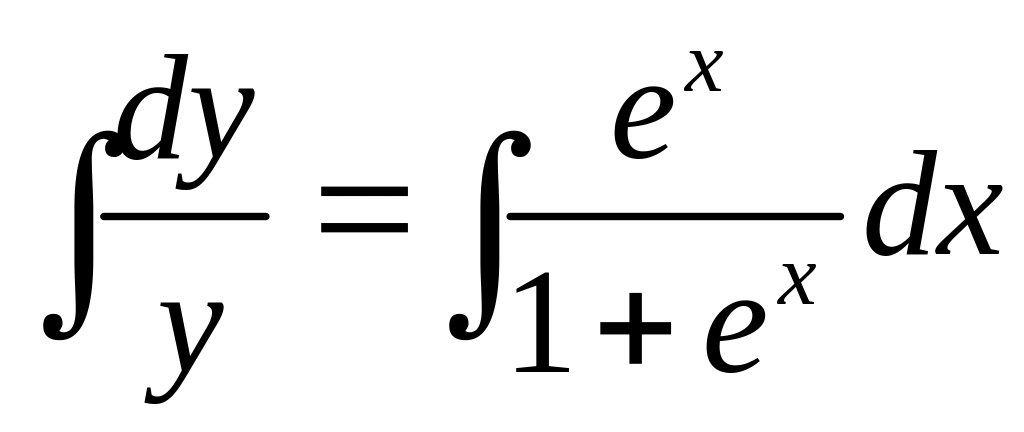Приведем схему вычисления интеграла

После вычисления интегралов имеем: , .

Потенцируя данное выражение, получаем . Отметим, что решение содержится в полученном выражении общего решения при С=0.

Ответ: .

Пример. Найти общий интеграл дифференциального уравнения

.

Тогда , . Заметим, что . Разделяем переменные:

.

Интегрируя правую и левую части, получаем

.

После вычисления интегралов имеем: .

Ответ: .

Пример. Найти общий интеграл дифференциального уравнения

.

Поясним, что такая запись подразумевает под дифференциал независимой переменной, под - дифференциал неизвестной функции ( = ).

Перенесем выражения, содержащие в левую часть уравнения, выражения, содержащие - в правую часть. После некоторых простых преобразований, получаем

.

Разделяем переменные

.

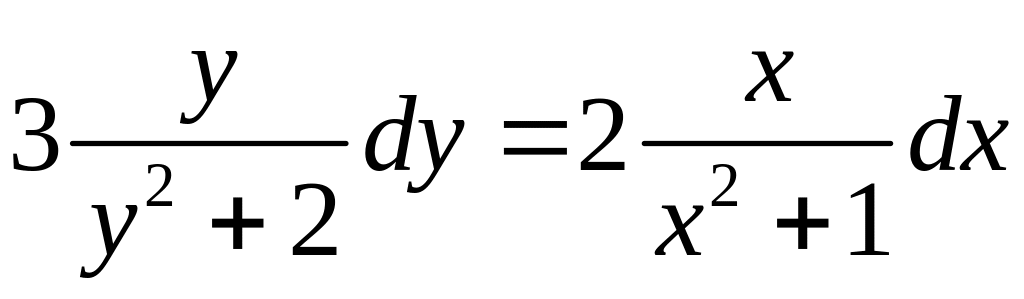Интегрируя правую и левую части, получаем .

Приведем схему нахождения интеграла

.

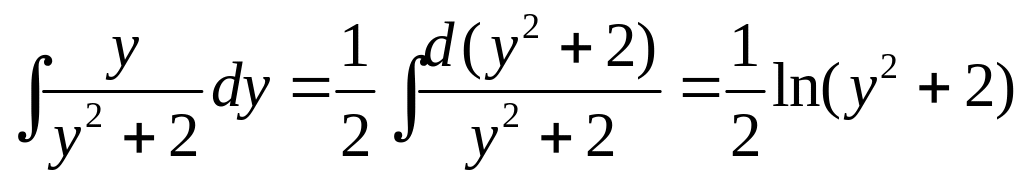После вычисления интегралов имеем

.

Потенцируя полученное выражение, имеем .

Ответ: .