Вопрос 13. Кривая нормального распределения.

Нормальное распределение,[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности распределения:

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ - стандартное отклонение(σ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Кривая нормального распределения (далее – КНР) – это теоретическая модель, представляющая собой абсолютно симметричное и гладкое распределение частот. Она имеет форму колокола и одну вершину, а ее концы уходят в бесконечность в обоих направлениях.

Главнейшим свойством КНР является то, что расстояние по абсциссе распределения (горизонтальная ось), измеренная в единицах стандартного отклонения от среднего арифметического распределения, всегда дает одинаковую общую площадь под кривой

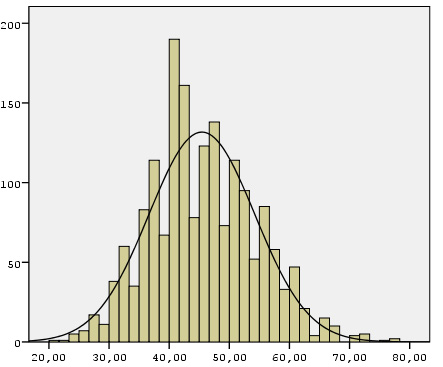
Вопрос 14. Ассиметрия и эксцесс. Z величины.

Показатели формы распределения, как и показатели вариации, также полезны для пони-

мания природы распределения переменной. Форму распределения оценивают с помощью

асимметрии и эксцесса.

Асимметрия. Асимметрия (skewness)

Характеристика распределения, которая оценивает симметрию расположения значений дан-

ных относительно средней. Распределение переменной может быть симметричным или асимметричным

(скошенным). При симметричном распределении частоты любых двух значений переменной,

которые расположены на одном и том же расстоянии от центра распределения, одинаковы.

Равны между собой также и значения среднего арифметического, моды и медианы. Распреде-

ление асимметрично (skewness), если значения переменной, равноудаленные от среднего, име-

ют разную частоту, т.е. одна ветвь распределения вытянута больше другой

Эксцесс (kurtosis) — это показатель относительной крутости (островершинности или плос-

ко верш и нности) кривой вариационного ряда по сравнению с нормальным распределением.

Эксцесс нормально распределенной случайной величины равен нулю. Если эксцесс положителен, то распределение более островершинно по сравнению с нормальным распределением. При

отрицательном значении распределение более плосковершинно по сравнению с нормальным,

Значение этой статистики для табл. 15.2 равно —1,261; это указывает на то, что распределение

более плосковершинное по сравнению с нормальным.

Эксцесс (kurtosis)

Мера относительной крутости кривой распределения частот.

15. Постановка и проверка гипотез.

Гипотеза – это не вопрос и не проблема, а утверждение.

Для статистической проверки выбирают гипотезы, отражающие самую общую ситуацию.

Альтернативная гипотеза – противоположная проверяемой.

Нулевой, основной или проверяемой гипотезой называется первоначально выдвинутая гипотеза, которая обозначается Н₀.

Конкурирующей или альтернативной гипотезой называется гипотеза, которая противоречит основной гипотезе Н0 и обозначается Н₁.

Проверка гипотезы. На основании экспериментальных данных вычисляется некоторая величина А. Предположим, что гипотеза верна и все обусловлено только статистикой.

По значению функции можно определить вероятность того, что в результате нашего эксперимента получится такое большое значение А (если гипотеза верна). Эта вероятность обозначается буквой p или α и называется уровнем значимости гипотезы.

Меньше нуля или больше 1 уровень значимости быть не может, поскольку это – вероятность.