23. Коэффициент линейной корреляции Пирсона

ПАРНАЯ КОРРЕЛЯЦИЯ

Часто при проведении маркетингового исследования нас интересует связь между двумя

метрическими переменными, как, например, в следующих ситуациях.

• Насколько сильно связан объем продаж с расходами на рекламу?

• Существует ли связь между долей рынка и количеством торгового персонала?

• Связано ли восприятие качества товаров потребителями с их восприятием цены?

В таких ситуациях наиболее широко используемой статистикой является коэффициент пар-

ной корреляции, г (product moment correlation г), который характеризует степень тесноты связи

между двумя метрическими (измеряемыми с помощью интервальной или относительной

шкал) переменными, скажем, Хп Y. Этот коэффициент используют, чтобы определить, суще-

ствует ли между переменными линейная зависимость. Он показывает степень, в которой ва-

риация одной переменной X связана с вариацией другой переменной Y, т.е. меру зависимости

между переменными Л" и Y.

Коэффициент парной корреляции г (product moment correlation r)

Статистический показатель, характеризующий степень тесноты связи между двумя метриче-

скими переменными.

Поскольку этот коэффициент первоначально предложил Карл Пирсон (Karl Pearson), его

также называют коэффициентом корреляции Пирсона. Кроме того, он известен как простой коэф-

фициент корреляции, линейный коэффициент корреляции или просто коэффициент корреляции,

Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. Линейный коэффициент корреляции — это показатель силы связи, описывающий линейную зависимость между двумя переменными

В общем виде формула для подсчета коэффициента корреляции такова:

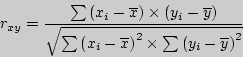
где   - значения, принимаемые переменной X,

 - значения, принимаемые переменой Y,

 - средняя по X,

 - средняя по Y.

24. Уравнение линейной регрессии

Регрессионный анализ (regression analysis) — это мощный и гибкий метод установления

формы и изучения связей между метрической зависимой переменной и одной или нескольки-

ми независимыми переменными.

Регрессионный анализ (regression analysis)

Статистический метод установления формы и изучения связей между метрической зависи-

мой переменной и одной или несколькими независимыми переменными.

Регрессионный анализ используют в следующих случаях.

1. Действительно ли независимые переменные обуславливают значимую вариацию зависи-

мой переменной; действительно ли эти переменные взаимосвязаны?

2. В какой степени вариацию зависимой переменной можно объяснить независимыми пере-

менными: теснота связи?

3. Определить форму связи: математическое уравнение, описывающее зависимость между за-

висимой и независимой переменными.

4. Предсказать значения зависимой переменной.

5. Контролировать другие независимые переменные при определении вкладов конкретной

переменной.

Хотя независимые переменные могут объяснять вариацию зависимой переменной, это не-

обязательно подразумевает причинную связь. Использование в регрессионном анализе таких

терминов, как зависимая или критериальная переменная и независимая переменная

(предиктор) отражает наличие математической зависимости между переменными. Данная тер-

минология не подразумевает существование причинно-следственной связи между перемен-

ными. Регрессионный анализ имеет дело с природой и степенью связи между переменными и

не предполагает, что между ними существует какая-либо причинная связь. Вначале мы обсу-

дим парную регрессию, а затем множественную.

ПАРНАЯ РЕГРЕССИЯ

Парная регрессия (bivariate regression) — это метод установления математической (в форме

уравнения) зависимости между одной метрической зависимой (критериальной) переменной и

одной метрической независимой переменной (предиктором). Во многом этот анализ аналоги-

чен определению простой корреляции между двумя переменными. Однако для того чтобы вы-

вести уравнение, мы должны одну переменную представить как зависимую, а другую — как

независимую.

Парная регрессия (bivariate regression)

Метод установления математической (в форме уравнения) зависимости между двумя мет-

рическими перемнными: зависимой и независимой.

Примеры, приведенные ранее при изучении простой корреляции, рассмотрим с точки зре-

ния регрессии.

Парный коэффициент корреляции г является мерой линейной связи между двумя метри-

ческими (измеренными интервальной или относительной шкалой) переменными. Его квадрат

г2 измеряет долю вариации одной из переменных, обусловленную вариацией другой. Частный

коэффициент корреляции — мера зависимости между двумя переменными после исключения

эффекта от влияния одной или нескольких дополнительных переменных. Порядок частной

корреляции указывает на количество переменных, на которые необходимо внести поправку

или которые следует исключить. Коэффициенты частной корреляции могут оказаться полез-

ными для выявления ложных связей.

С помощью парной регрессии устанавливается математическая зависимость (в виде урав-

нения) между метрической зависимой (критериальной) переменной и метрической независи-

мой переменной (предиктором). Уравнение описывает прямую линиию, и для его вывода ис-

пользуют метод наименьших квадратов. В случае построения регрессии с нормированными

данными отрезок, отсекаемый на оси OY, принимает значение, равное 0, и коэффициенты рег-

рессии называют взвешенными "бета"-коэффициентами. Силу тесноты связи измеряют ко-

эффициентом детерминации г, который получают, вычисляя отношение SSpeefW к SSr Стан-

дартную ошибку уравнения регрессии используют для оценки точности предсказания, и ее

можно интерпретировать как род средней ошибки, сделанной при теоретическом предсказании

Y, исходя из уравнения регрессии.