20. Коэффициент контингенции. Кэффицент Юла. Коэффициенты детерминации.

В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые  непараметрические методы.

Коэффициент контингенции. Этот коэффициент используется для выяснения связи между признаками, не имеющими количественного выражения (альтернативная вариация, или изменчивость качественных признаков): 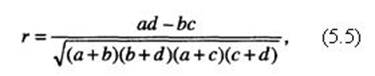   где а, b, с, d – значения в клетках таблицы распределения (корреляционной таблицы), имеющей следующую конфигурацию:

a	b
c	d

В таблице в клетках последовательно размещаются значения совместных (отвечающих как одному, так и другому признакам) частот, относящихся к двум качественным признакам, полученные при двух группах наблюдений. Наличие в наблюдениях признака x обозначается 1, его отсутствие – 0; наличие в наблюдениях признака у – 0, а отсутствие – 1. Раскроем эту таблицу.    Коэффициент ассоциации Юла. 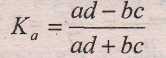Он также используется для четырехклеточной таблицы и рассчитывается по формуле  Коэффициент контингенции равен 1 лишь в том случае, если а и d или b и с одновременно равны 0. В отличие от этого коэффициент ассоциации Юла равен 1 уже в случае, если одно из чисел в клетках таблицы оказалось равным 0. Величина коэффициента контингенции всегда ниже величины коэффициента ассоциации.  Во всех случаях величина коэффициента корреляции зависит от выбора единицы наблюдения. Если она делится, дробится, расчленяется, то повышается влияние случайностей и теснота связи приуменьшается. Когда единица наблюдения укрупняется, то влияние случайностей уменьшается и теснота корреляционной связи преувеличивается.  С помощью приведенных способов расчетов выявляется мера тесноты связи признаков, мера их взаимного варьирования в выбранных статистических рядах данных без специального анализа формы связи между этими рядами. Знание прошлого и будущего, прогноз перемен в связи с изменениями в тех или иных условиях существования нуждаются в выявлении формы связи явлений и соответствующих показателей корреляции. 

Коэффициент детерминации. Тесноту связи измеряют коэффициентом детерминации г2. Он

колеблется в диапазоне между 0 и 1 и указывает на долю полной вариации У, которая обуслов-

лена вариацией X.

Для оценки качества модели используют коэффициент детерминации. Долю дисперсии, которая обусловлена регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R2.

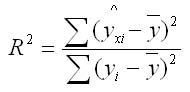
Коэффициент детерминации, как и коэффициент корреляции, принимает значения от -1 до +1. Чем ближе его значение коэффициента по модулю к 1, тем теснее связь результативного признака Y с исследуемыми факторами X.

Например, если получают коэффициент детерминации R2 = 0,9, значит уравнением регрессии объясняется 90% дисперсии результативного признака, а на долю прочих факторов приходится 10% ее дисперсии (т.е. остаточная дисперсия). Величина коэффициента детерминации служит важным критерием оценки качества линейных и нелинейных моделей. Чем значительнее доля объясненной вариации, тем меньше роль прочих факторов, и значит, модель регрессии хорошо аппроксимирует исходные данные и такой регрессионной моделью можно воспользоваться для прогноза значений результативного показателя.