12.Корреляционно-дисперсионный анализ переменных, выраженных количественными и качественными показателями.

Обычно связи между экономическими характеристиками отражают причинно-следственную структуру процесса. При изучении связей основная проблема состоит в том, что на начальных этапах многомерного статистического анализа причинно-следственная структура практически неизвестна. Для оценивания причинно-следственных связей используются методы корреляционно-дисперсионного анализа (КДА).

Оценивание причинно-следственных связей требует решения следующих задач:

1. Выбор числовой характеристики, отражающей статистическую связь признаков;

2. Количественная оценка характеристики связи по выборке;

3. Проверка гипотезы о том, что полученное числовое значение является статистически значимым;

4. Определение структуры связи между множеством признаков.

Корреляционно-дисперсионный анализ количественных данных:

При рассмотрении количественных переменных основное внимание уделяется линейным связям, где базовым инструментом измерения является парный коэффициент корреляции 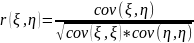, r от -1 до 1.

Статистическая значимость парного коэффициента корреляции устанавливается следующим образом с помощью критерия Стьюдента:

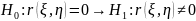
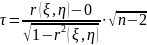
Если 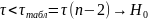верна, 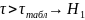верна.

Обобщением парного коэффициента корреляции (например, в случае многомерных статистических измерений) является коэффициент множественный корреляции Rх0х1…хn=Ry/R признака Х₀ с набором признаков {Х₁; …; Х_m}: 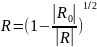, где 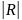- определитель матрицы парных корреляций {Х₁; …; Х_m}, а 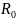– матрица парных корреляций признаков {Х₀; Х1; …; Х_m}

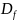Более универсальным индикатором связи является коэффициент детерминации R², который показывает «долю» связи между Х₀ и набором признаков {Х₁; …; Х_m}, объясненную линейной регрессией. , где В – дисперсия Х₀, а - дисперсия 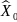линейной регрессионной модели: 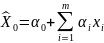. Чем больше R², тем сильнее линейная составляющая связи.

Статистическая значимость коэффициента детерминации устанавливается следующим образом с помощью критерия Фишера:

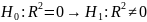
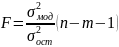
Если 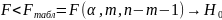верна, 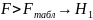верна.

Корреляционно-дисперсионный анализ порядковых данных:

Чаще всего порядковые данные в социально-экономических исследованиях получают в результате экспертного оценивания. При экспертном оценивании структура данных усложняется дополнительным измерением и таблица данных трансформируется в трехмерный параллелепипед «объект – признак – эксперт».

Основной «единицей» КДА порядковых данных является ранжировка r = 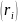, где 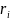– ранг i-ого объекта.

Мнение эксперта по всем признакам можно представить матрицей 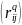рангов i-го объекта по j-му признаку. На множестве ранжировок можно ввести понятие расстояния d.

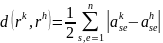,где 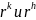- ранжировки, данные k- м и h-м экспертом. Расстояние должно удовлетворять основным свойствам:

• неотрицательность

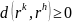
• симметричность

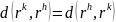
• правильно треугольника

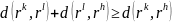
Аналогом парной корреляции как меры связи в случае порядковых данных является понятие ранговой корреляции, которое позволяет оценить степень согласованности мнений двух экспертов.

Коэффициент ранговой корреляции по Спирмену

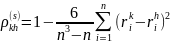. Этот коэффициент позволяет измерить парную связь при отсутствии связанных рангов.

Если существуют связанные ранги, то это приводит к смещению коэффициента. Для устранения эффекта используют модифицированный коэффициент Спирмена для связанных рангов:

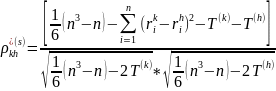
Коэффициенты связанности Т вычисляются по формуле

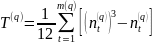, где

t – номер группы связанных рангов;

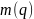- число групп связанных рангов;

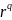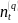, –число элементов, входящих в t-ю группу связанных рангов ранжировки

Критериальная проверка значимости коэффициента :

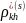H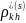₀ = = 0; 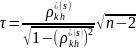. Расчетное значение сравнивается с квантилями распределения Стьюдента на выбранном уровне значимости .

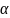Вторым способом измерения связи является коэффициент ранговой корреляции Кендалла, который в случае отсутствия связанных рангов вычисляется по формуле

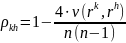
, где 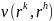минимальное число перестановок соседних элементов ранжировки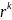 , необходимых для приведения ее к ранжировке .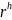

При наличии связных рангов коэффициент Кендалла имеет вид:

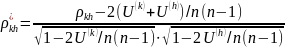
, где 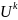– коэффициент связности

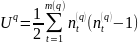
Критериальная проверка:

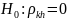
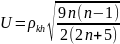
Если 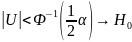. Коэффициенты ранговой корреляции изменяются от 1 до 1.