11.Однофакторные стохастические процессы. Основные виды моделей. Выбор аналитической формы модели. Оценка параметров и критериальная проверка качества модели.

Примерами таких процессов служат цены на товары, финансовые активы, доход предприятия и др.

Различают стационарные и нестационарные процессы.

Стационарность в узком (строгом) смысле – процесс 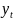стац. В узком смысле, если совместное распределение значений 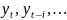совпадает с совместным распределением при любых .

Стационарность в широком смысле предполагает соблюдение условий постоянства мат. ожидания, дисперсии, автокорреляционной функции процесса вне зависимости от интервала времени, на котором они определялись.Тестирование стационарности проводится с помощью непараметрич. тестов (ЗР не известен- тесты Манна-Уитни, Сиджела-Тьюки) полупараметрич. И параметрич. тестов (Стъюдент, Фишер, Кокрен, Бартлетт). Если нестационарный ряд, то приводим к стационарному с помощью преобразований.

Модели стационарных временных рядов:

Модели авторегрессии (АР)

Общий вид модели авторегрессии k-го порядка – АР(k):

,

Где - случайная ошибка с нулевым мат. ожиданием, конечной дисперсией и единичной автокорреляционной матрицей, свидетельствующей об отсутствии автокорреляционной связи между рядами ошибки , т.е. . Без ограничения общности будем полагать, что

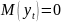
Для оценки параметров модел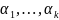и , выразим их через коэффициенты автокорреляции :

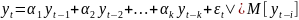
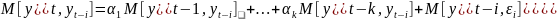
- ковариация

(1)

Подставляем выборочные оценки коэфф. Автокорреляции ri, получаем сис-му ур-й Юла-Уокера:

Оценки находятся на основе определителей:

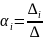
Теоретически оценки должны обладать св-ми несмещенности и эффективности, однако на практике св-ва могут не поддерживаться. Качество оценок может быть проверено путем исследования свойств ряда ошибки . Если ее св-ва близки к характеристикам белого шума, то оценки можно считать приемлимыми. Для этих целей могут использоваться критерий Дарбина-Уотсона и другии мощные критерии, например Бартлетта, Тейла. Эффективность использования моделей АР может быть установлена путем сопоставления дисперсии исходного процесса и дисперсии ошибки модели. Хотя в моделях стационарных временных рядов нельзя ожидать значительного уменьшения дисперсии ошибки по сравнению с дисперсией процесса.

Автокорреляционные функции моделей АР представляют собой набор коэффициентов автокорреляции, зависящих от сдвигов. Значения этих коэффициентов можно опр., используя соотношение (1). В частности для модели АР(1) коэфф. автокорреляции уменьшаются по экспоненте с ростом сдвига i, для АР(2) – затухающая экспонента или затухающая синусоида.

Частную автокорреляционную ф-ю модели АР(k)образуют последние значения коэфф. моделей авторегрессий порядков, не превосходящих k, поэтому оценки значений кофф. частной автокоррел. ф-и сами являются СВ и характеризуются ошибкой. Значимость этих коэфф. Может быть оценена по критерию Стъюдента.

Модели скользящего среднего МА

В моделях скользящего среднего текущее значение стационарного процесса 2-го порядка yt представляется в виде линейной комбинации текущего и предшествующего значения ошибки , по своим св-м, соответствующей белому шуму:

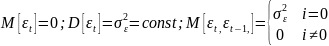
Модель МА(m):

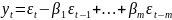
Где - параметры модели, -ошибка модели в момент t, m=1,2,… – порядок скользящего среднего.

Для оценки параметров модели выразим их через коэффициенты автокорреляции :

;

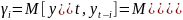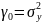
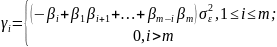
Т.о. автокорреляционная ф-я модели равна 0 после задержки m (обрывается на задержке m).

Вместо значений 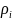подставляем их выборочные значения ri:

Решаем нелинейную систему уравнений на основе специальных итеративных процедур расчета, за исключением простой модели МА(1), МА(2), и находим неизвестные параметры

Для моделей скользящего среднего МА(k) могут быть построены автокорреляционные функции, поведение которых совпадает с поведением частных автокоррел. ф-й АР(k) при одинаковых индексах k=1,2,3,…

Модели авторегрессии-скользящего среднего АРСС(k,m)

Где 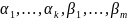- k=1,2,… параметры модели, рядок авторегресси, m=1,2,… – порядок скользящего среднего.

Запишем ур-е в виде:

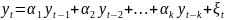
При i>m значения коэффициентов автокорреляции модели АРСС(k,m) удовлетворяют св-м, характерным для коэффициентов модели АР(k):

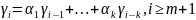
Коэффициенты можно найти из сис-мы Юла-Уокера.

С использованием найденных коэфф. Сформируем процесс СС(m):

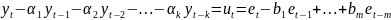
Для определения оценок коэфф. применяются нелинейные методы оценивания, предполагающие решение сис-мы нелинейных ур-й. Из полученных результатов вытекает, что коэффициенты автокорреляции модели АРСС(k,m), начиная с (m+1)-го индекса ведут себя , как коэфф. АР(k), начиная с 1-го индекса. При этом частная автокорреляц. функция этой модели обрывается на (m+1)-й задержке.

В случаях, если модель АРСС была построена для временного ряда, приведенного к стационарному путем преобразований, необходимо выполнить обратное преобразование с помощью оператора сдвига B (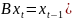 . После чего провести проверку качества восстановленной модели:

1. провести анализ св-в восстановленной ошибки с использованием известных тестов- в идеальном случае, ошибка - белый шум

2. желательно, чтобы дисперсия ошибки была меньше дисперсии процесса

Выбор модели:Необходимо выбирать модель с наименьшим числом параметров (минимальным порядком). При выборе модели стоит также руководствоваться св-ми автокорреляционной и частной автокорреляционной ф-й.

Автокорр. ф-ия АР(1) спадает строго по экспоненте. При порядках моделей АР больше 1 более информативными являются коэфф. их частных автокоррел. ф-й. Поведение частной автокорр. ф-ии АР аналогично поведению автокорр. ф-ии МА. Для модели АР(k) ее часная автокорр. ф-я обрывается после задержки k, как у автокоррел. ф-и модели СС.

Нестационарные процессы характерны для финансовой сферыГСБ-1 – динамика приростов цен по своисв- соответствует процессу «строгого белого шума». Нормальный ЗР приростов.ГСБ-2 – смягчение ГСБ-1, ЗР прироста цен может меняться ГСБ-3 – смягчение ГСБ-2, автокорреляция между приростами отсутствует, однако автокорреляция между их степенями может иметь место.