30. Примеры законов распределений ущербов и особенности их использования в оценках технологических, операционных рисках, рисках ошибок персонала, рыночных рисках.

Статистические методы построения вероятностных законов проявления событий и ущербов.

Использование статистических методов при построении законов распределения событий и уровней ущербов базируется на предположении, что наблюдаемые частоты этих случайных явления отражают определенные временные или пространственные закономерности. Это соответствие может быть установлено путем сопоставления наблюдаемых частот и теоретических значений вероятностей соответствующих случайных величин, определяемых из предполагаемого закона. Такое сопоставление может быть осуществлено на основе критерия Пирсона ( ).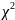

Оценка этого критерия для распределения ущерба может быть получена на основе следующего выражения:

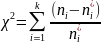
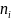- наблюдаемое число проявлений случайной величины (т.е. i-ый уровень ущерба)

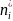- число проявлений , определенное на основе предполагаемой плотности вероятности,

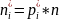, где n – общее число испытаний, а 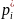- теоретическая вероятность события .

Выражение получено из предположения, что величина распределена по нормальному закону. .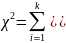

Среди законов распределения вероятностей, которым подчиняются распределения неблагоприятных событий оп их силе, например, производственные аварии, природные катастрофы, противоправные действия в отношении предприятия, террористические акт и т.п., выделим законы Пуассона – полиномиальный и экспоненциальный. Они часто используются при описании условных распределений ущербов.

Для оценки вероятностей редких, но значительных по силе событий (землетрясения, прорывы дамб, крупные дефолты), используются законы распределения Вейбула, логарифмический нормальный, Парето, Коши и некоторые другие.

Согласно закону Пуассона вероятность числа неблагоприятных событий в единицу времени (обычно год) определяется следующим выражением:

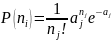, где 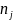- число событий j-го вида, а 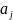- среднее число таких событий.

Полиномиальный закон распределения используется для оценки вероятностей проявления ряда взаимоисключающих событий (различной силы), ущербов (различающихся по величине). Пусть неблагоприятное событие j-го вида в единичном интервале времени (t, t+1) имело место 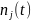раз, а за T интервалов наблюдения t = 1, …, T- раз, где .

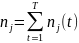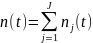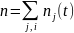Тогда и определяют общее число событий за интервал t и T временных интервалов соответственно.

В соответствии с биномиальным распределением в предположении о неизменности причин, определяющих частоту проявления событий j-го типа, вероятности его проявления 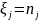раз, = 0, 1, …, n определяются согласно следующему выражению:

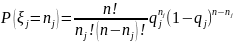, где 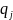- вероятность проявления события j-го типа.

Экспоненциальное распределение с плотностью 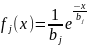(0<x<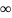 )также часто подходит для описания условного распределения ущербов x при проявлении событий различной силы. Константа 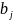является математическим ожиданием ущерба при проявлении события силы j.

Эконометрические методы оценки распределений ущербов в случае рыночных рисков.

К группе рыночных рисков обычно относят процентный, валютный, ценовой, кредитный, инвестиционный и прочие виды рисков, существование которых обусловлено неблагоприятными изменениями стоимостных показателей рынка, влияющих на результаты текущей деятельности объекта. В общем случае такие риски характеризуются возможной потерей прибыли предприятия, обусловленной неблагоприятными изменениями цен на производимую продукцию.

Влияние этих рисков на суммарный риск рыночной деятельности можно с некоторой долей условности отобразить с помощью индексного метода.

Обозначим через фактические цены на проводимые операции, 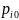- плановые, – объемы операций, i – индекс ресурса. Тогда уровень потерь дохода предприятия можно оценить с помощью индекса цен .

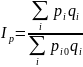Уровень ценового риска компании определяется разностью между числителем и знаменателем, умноженной на вероятность 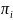отклонения цен в неблагоприятном направлении: , > .

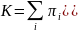Средний ценовой риск можно оценить с использованием следующего подхода. Предположим, что известен закон распределения цены 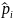на определенный вид товара. Выразим его через функцию плотности 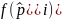. Тогда потери компании будут определены в области 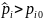. Для этой области можно оценить среднюю величину фактической цены согласно следующему выражению: .

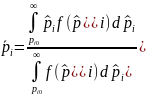Предположим, что в условиях стабильного рынка сила воздействия каждого отдельного фактора мала, а компания не ошибается в оценке уровня цен. Поэтому цены имеют нормальный закон распределения:

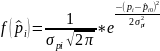
Аналитические методы построения вероятностных распределений событий и ущербов.

При недостаточности исходной информации о частоте и последствиях неблагоприятных событий, но при наличии научно обоснованных гипотез о вероятностных закономерностях их проявления соответствующие плотности вероятностей могут быть построены на основе аналитических методов. Эти методы нашли широкое применение при оценке вероятностей редких, но значительных событий, и связанных с ними законов распределения ущерба. Примеры: землетрясения, пожары, наводнения, дефолты и т.д.

Оценка вероятности редкого события на основе экстраполяции закона распределения базируется на следующих предположениях. Пусть, вероятность редкого события определена следующим уравнением: , где - известное граничное значение ущерба, превышение которого характерно для редкого, но сильного события. Далее полагается, что предел находится на «хвосте» известного закона распределения, описывающего распределение вероятностей в зависимости от ущерба на всем множестве его возможных значений. В таком случае вероятность редкого события может быть определена на основе следующего известного выражения: , где – плотность предполагаемого закона распределения с известными параметрами.

Функция строится на множестве известных значений x в предположении, что она окажется справедливой и за пределами этого множества, т.е. на «хвосте распределения».

В частности, функция плотности распределения Вейбулла зависит от трех параметров: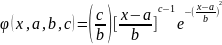 , где и a – определяет величину сдвига на оси ущербов.

Функция плотности логарифмически нормального закона распределения имеет следующий вид: 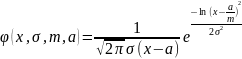, где х – величина ущерба, m – параметр масштаба (m>0), – среднеквадратическое отклонение логарифма случайной величины x-lnx, a – параметр сдвига.

В этом случае вероятность неблагоприятного события с ущербом (силой), превышающим , определяется по следующей формуле:

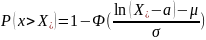, где Ф – функция Лапласа (табличное значение нормального закона распределения).

Во многих исследования катастрофических, аварийных событий в сложных системах часто используется степенной закон распределения вероятностей, ставящий значение вероятности события в зависимости от его силы, ущерба, который оно вызывает. Общий вид функции плотности степенного закона распределения может быть выражен следующей формулой: 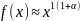, где 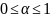- константа.

Функция плотности, определенная этим выражением, соответствует функции распределения Парето, вид которой задается выражением

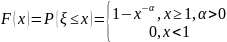
Распределение Парето выражает то обстоятельство, что в ряду ущербов от катастроф редко, но наблюдаются сверхэкстремальные уровни, несоизмеримые по величине со значением ущербов для подавляющей части подобных событий.

Толстые хвосты распределений предопределяют необходимость использования специальных приемов при оценке их параметров.

Например, согласно методу максимального правдоподобия оценка параметра распределения Парето определяется по следующему выражению: .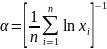

В качестве среднего квадратического отклонения полученного значения обычно используется показатель 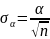. Используя степенные распределения (распределение Парето) в риск-анализе, необходимо также учитывать ограниченность масштабов ущербов при тех или иных событиях. Из-за редкости значительных по силе катастроф существующая статистика мало чем может помочь при оценке предельной величины ущерба. Этот предел проще определить экспертным путем либо на основе аналитических оценок. В частности, при больших значениях n величину 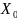, превышающие которую ущербы рассматриваются как невозможные, предлагается определять из соотношения .

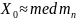Выполнение условия 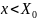обеспечивается «обрезанием» хвоста распределения Парето. В этом случае функция распределения определяется, например, следующим выражением: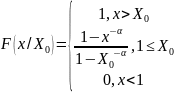 . Таким образом, функция плотности степенного распределения, с усеченным хвостом определяется следующим отношением:

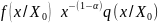
31. Анализ риска ликвидности и неплатежеспособности.  Анализ ценового риска в портфеле производных финансовых инструментов.

Риск ликвидности характеризует возможность потерь в результате:

1. Изменений спроса и предложения, затрудняющих продажу или покупку активов (рыночная ликвидность)

2. Возникновение дефицита наличных средств или иных высоколиквидных активов для выполнения обязательств перед контрагентами (внутренняя ликвидность).

Общие причины риска рыночной ликвидности:

• Разница между спросом и предложением;

• Разница цен покупки и продажи;

• Смена торговой площадки;

• Реализация операционных и кредитных рисков и др.

В целом, на формирующихся рынках риски ликвидности всегда выше, чем на сформировавшихся, вследствие несбалансированности рын.механизмов, снижающих их устойчивость.

Управление риском рыночной ликвидности включает:

1. Оптимизацию портфеля (долгосрочных контрактов и рын.позиции)

2. Хеджирование и работу с производными инструментами

3. Самострахование (создание резервного фонда);

4. Диверсификацию

Внутренний риск ликвидности часто бывает обусловлен кредитным риском, а также технологическим риском и риском корпоративного управления. Управление этим риском базируется на контроле за финансовыми потоками (ведение графика платежей по поступлениям/списаниям, установление операционных лимитов) и вкл. Меры:

1. Лимитирование объемов договоров на поставку продукции и оборудования;

2. Резервирование средств для обеспечения ликвидности;

3. Стресс-тестирование;

4. Управление, влияющими рисками.

Риск неплатежеспособности – риск невыполнения организацией своих обязательств перед контрагентом в силу нехватки наличных средств или других высоколиквидных активов.

В каждый момент времени можно точно сказать, платежеспособна компания или нет. Основными факторами, влияющими на риск неплатежеспособности, являются возможность компании привлекать заемные средства и самостоятельно генерировать денежный поток путем продажи собственных активов.

Выделяют 3 источника возникновения риска неплатежеспособности:

• системный риск возникает в случае, когда в расчетных системах нет необходимого кол-ва ден. средств или из-за сбоев в функционировании таких систем средства не будут в указанные сроки переведены по назначению.

• индивидуальный риск состоит в возможном изменении мнения участников рынка о платежеспособности компании и соответствующем пересмотре отношений с ней. технический риск состоит в несбалансированной структуре будущих платежей (наиболее серьезная составляющая риска неплатежеспособности, поскольку компания не может держать в качестве ликвидных средств наличность без уменьшения рентабельности своей деятельности)

Компания может ограничить риск неплатежеспособности, поддерживая необходимое кол-во ликвидных активов, однако их избыток ведет к недополучению компанией прибыли. Кроме того, на риск неплатежеспособности влияет скорость, с которой компания может превратить ликвидные активы в наличные средства. В кризисной ситуации продажа даже самых ликвидных активов может занять или слишком долго времени, или не принести ожидаемого денежного потока.

Ценовой риск является основной составляющей рыночного риска и характеризуется неблагоприятными для компаний отклонениями цен. Является спекулятивным по своей природе.

Различают ценовой риск рынка акций (или фондовый риск), ценовой риск товарных рынков (или товарный риск), риск рынка производных финансовых инструментов.

К фундаментальным причинам ценового риска относятся: короткие и длинные позиции, спрос и предложение, эластичность цены, рыночная сила; к текущим – товарные сделки и воздействие рынка производных инструментов, влияние новостного фона, наличие инсайдерской информации, поведение конкурентов.

Управление ценовыми рисками включает повышение точности и обоснованности прогнозов состояния рынка, планов производственной и сбытовой деятельности, использование инструментов страхования, хеджирования и др. стратегии.

Показатели риска на финансовых рынках:

• на рынке инструментов с фиксированным доходом – дюрация;

• На рынке акций – коэффициент бета;

Пример, показатель дельта измеряет величину изменения стоимости данного финн. Инструмента V при малом изменении базового ценового фактора r (например, ставки процента или цены базового актива):

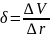
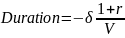
Дюрация позволяет упрощенно оценить степень зависимости рыночной цены инструмента от изменения процентной ставки. Чем больше дюрация инструмента, тем значительнее изменения ее рыночной стоимости при изменении процентных ставок, то есть тем выше процентный риск.

Подход VaR

VaR – это выраженная в данных денежных единицах (базовой валюте) оценка величины, которую не превысят ожидаемые в течение данного периода времени потери с заданной вероятностью.

Пусть фиксирован некоторый портфель открытых позиций. VaR портфеля для данного доверительного уровня (1-а) и данного периода поддержания позиций t определяется как такое значение, которое обеспечивает покрытие возможных потерь x держателя портфеля за время t с вероятностью (1-а):

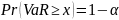
Как следует из определения, величина VaR для портфеля заданной структуры – это наибольший ожидаемый убыток, обусловленный колебаниями цен на финансовых рынках, который рассчитывается:

• на определенный период времени в будущем (временной горизонт);

• с заданной вероятностью его непревышения (уровень доверия);

• при данном предположении о характере поведения рынка (метод расчета).

Доверительный интервал и временной горизонт являются ключевыми параметрами, без которых невозможны ни расчет, ни интерпретация показателя VaR. Так, значение VaR в 10 млн.руб. для временного горизонта в один день и доверительного интервала 99% будет означать (при условии сохранения тенденций рыночной конъюнктуры), что вероятность того, что в течение след. 24 часов мы потеряем меньше чем 10 млн. руб., составляет 99%;

В настоящее время основными, классическими подходами к оценке VAR считаются:

• метод исторического моделирования,

• метод параметрической оценки, наиболее распространенный в форме вариационно-ковариационной модели,

• метод имитационного моделирования, часто именуемый по основной применяемой в его рамках модели методом Монте-Карло

Показатель VaR используется в риск-менеджменте в следующих целях:

• для расчетов лимитов по открытым позициям;

• для расчета достаточности капитала и распределения капитала между направлениями бизнеса;

• для оценки доходности операций с учетом риска.

При использовании любого из перечисленных подходов модель расчета VaR необходимо верифицировать во избежание риска применения неадекватной модели.