Тест 1.
Если в модели опущена переменная, которая должна быть включена, то оценки коэффициентов регрессии могут оказаться смещенными
Проблемой спецификации не является расчет оценок параметров эконометрической модели
Один из этапов построения эконометрической модели, на котором проверяются статистические свойства построенной модели, называется … верификацией.
Качество регрессионной модели ухудшается в случае _____ количества оцениваемых параметров при _____ объёме выборки большого,небольшой |
|
|
верификацией модели |
Объем выборки для построения эконометрической модели ограничен сверху объемом генеральной совокупности
|
Эконометрика синтезирует в себе науки: |
|
экономическую теорию, математическую статистику и экономическую статистику
Эконометрическая модель - это математическая Модель |
Реальной экономической системы (объекта), построенная на статистических данных
Спецификацией эконометрической модели является математическая форма записи уравнения зависимости переменной у от одного или нескольких факторов х
Формализация закономерностей общей экономической теории является одним из принципов ______ эконометрической модели спецификации
Вопрос |
Пусть истинной
моделью является |
|
оценки b2 и b3 будут такими же, как и при построении регрессии с использованием
|
(х1,
х2, х3 -
существенные факторы), однако, мы не
имеем статистических данных по
переменной 
.
Но другая переменная 
выступает
идеальным заменителем для нее в том
смысле, что имеется строгая
(функциональная) линейная связь 
,
где 
и 
являются
постоянными, но неизвестными величинами.
Если мы построим регрессию 
,
то
Тест 4.
К причинам присутствия в эконометрической модели случайного фактора относятся:
-невозможность включения в модель всех объясняющих переменных
-стохастический характер зависимости
В линейном уравнении парной регрессии
В эконометрическую модель множественной регрессии необходимо включить факторы, оказывающие ________ влияние на исследуемый показатель существенное
Верным является утверждение, что параметр Регрессии является детерминированной величиной, а его оценка – случайной
В частном уравнении регрессии факторных переменных ___________ по сравнению с исходным уравнением множественной регрессии, по которому оно построено всегда меньше |
переменными
являются x,y
В линейном уравнении парной регрессии переменными не являются a b
|
|
В линейном уравнении
множественной регрессии |
|
коэффициентами
регрессии являются b1
b2
Линейное уравнение множественной регрессии
имеет вид
какой из
факторов сильное влияние на у по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой
В линейной регрессии Y=b0+b1X+e переменными уравнения регрессии являются x y
|
.
Определите
или 
оказывает
более
.
Тест 5.
При оценке параметров линейного уравнения
регрессии метода наименьших квадратов определяют минимальное значение величины :
|
с
помощью
,где
Для определения оценок коэффициентов линейного уравнения регрессии использовать метод наименьших модулей, наименьш квадратов
При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной y не может определяться на основании _______ уравнения регрессии
нелинейного
дифференцированного
Метод наименьших квадратов предназначен для оценки параметров линейной эконометрической модели на основании результатов наблюдений, содержащих случайные ошибки
При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной y может определяться на основании _______ уравнения регрессии
линеаризованного
линейного
Пусть
тогда суть метода наименьших квадратов (МНК) состоит |
–
фактические значения,
–
расчетные значения
для i-го
наблюдения,
в
минимизации функции
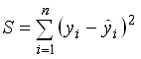
Для линейной регрессионной зависимости система нормальных уравнений линейная относительно параметров регрессии
Название метода «метод наименьших квадратов» подразумевает, что сумма квадратов отклонений значений результирующего признака от теоретических должна быть минимальной
В рамках метода наименьших квадратов (МНК) система нормальных уравнений – это система, решением которой являются оценки параметров теоретической модели
Метод наименьших квадратов применяется для ---выбора оптимальной линии из всех возможных -для описания линейной зависимости некоторого поля корреляции