
- •4. Rl тізбегін тұрақты кернеу көзімен қосу.
- •5.Rc тізбегінің өтпелі кезеңі. Қысқа тұйықталуы.
- •6. Rc тізбегін синусоидалы кернеу көзіне қосу
- •7. “Rlc” тізбегінің өтпелі кезеңі (тізбектей қосу)
- •8)Rlc тізбегін тұрақты кернеу көзіне қосу.
- •10. Сыйымдылықтың опериодикалық және тербелмелі разряды.
- •14. Эквивалентті операторлық сұлбалар
- •17)Импульсті өтпелі сипаттаманы қолданып, Дюамель интегралын шығару.
- •18 Жүйенің сип теңдуін құру ж,е түбірлерін анықтау
- •21. Операторлық беріліс фун-лары.
- •27.Біртекті желідегі қалыптасқан режим.
- •31. Дифференциалды және интегралды тізбектер. Толқындық кедергі және таралу еселеуіші
- •34.Біртекті желідегі қалыптасқан режим.
- •35.Желінің кіріс кедергісі толқын ұзындығы фаза жылдамдығы шағылысу еселуешісі:
- •40. Сызықсыз электр тізбегін екі түін потенциал әдісімен есептеу.



 1
Электр тізбегінің өтпелі кезеңі.
Комутация заңдары. Өтпелі
кезең активті және пассивті элементтердегі
ток пен кернеудің өзгеруі жәнеде алғашқы
еріксіз режимге өтуді ацтады. Осы кезде
коммутация орындалады. Коммутация әр
тізбекте активті жне пассивті
элементтерден тұратын тармақта қосылып
өшсе сонымен қатар тізбектің бір
бөлігінде қысқа тұйықталу, параметрлерінің
өзгерісі болғанда пайда болады. Сонымен
ол кілттің ашылып жабылуы.
1
Электр тізбегінің өтпелі кезеңі.
Комутация заңдары. Өтпелі
кезең активті және пассивті элементтердегі
ток пен кернеудің өзгеруі жәнеде алғашқы
еріксіз режимге өтуді ацтады. Осы кезде
коммутация орындалады. Коммутация әр
тізбекте активті жне пассивті
элементтерден тұратын тармақта қосылып
өшсе сонымен қатар тізбектің бір
бөлігінде қысқа тұйықталу, параметрлерінің
өзгерісі болғанда пайда болады. Сонымен
ол кілттің ашылып жабылуы.
Кілттің орналасуына б/ы түрі: 1
Кам кейн мезет 1) (0- ) ком дейн кілт ашық. 2) (0+ ) ком кейн кілт жабық.


 2
а)
ком дейн килт жабык б) ком кейн килт
ашық.
Егер t(0-
)
болсы. Бұл ком дейнгі уақыт. Егер t(+
)
болса. Бұл ком кейнгі алғашқы момент
уақыты. Егер t(0) болса, ком кезі д.а. Егер
t=͚ϖ
болса, еріксіз режим д.а.
2
а)
ком дейн килт жабык б) ком кейн килт
ашық.
Егер t(0-
)
болсы. Бұл ком дейнгі уақыт. Егер t(+
)
болса. Бұл ком кейнгі алғашқы момент
уақыты. Егер t(0) болса, ком кезі д.а. Егер
t=͚ϖ
болса, еріксіз режим д.а.
Ком заңдары: 1 заңы Ком дейнгі катушкадағы ток ком кейнгі катушкадағы токка тең. iL (0-)=iL(0+) Wm=Ldi/dt. 2 заңы Ком дейнгі конденцатордағы кернеу ком кейнгі конденцатордаңы кернеуге тең. UC(0-)=UC(0+) WE=CU2/2. Ком кезінде ток секірмелі болады. Индуктивтілік элементі Wm=Ldi/dt. Шексіз үлкен болады, және Кирхгофтың 2 заңымен анықталады. Егер конденсатор зарядталмаса кернеуге қосылмаса онда конденсатордағы кернеу ком кезінде 0 ге тең. Егер ком кезінде конденсатордағы кернеу секірмелі болса онда конденсатордағы ток iC=Cdt/dt. Шексіз үлкен болады. Бастапқы шарт уақыт t=0 кезде индуктивтілік элементіндегі өтпелі токпен конденсатордағы кернеудің мәндері ком кезінде секірмелі өзгермейтін мәндер. Тәуелсіз БШ
iL(0-)=iL(0+)=iL(0).
UC(0-)=UC(0+)=iC(0).
Тәуелді БШ Тәуелсіз БШ арқылы Кирхгофтың 1,2 заңды кез-клген құрылған теңдеу арқылы анықталады.
2.
Өтпелі кезеңнің қалыптасқан және еркін
режимі.
Егер
эл тізбегі тұрақты кернеу көзіне
қосылса, онда бұл тізбекте ағып жатқан
өтпелі ток, лездік мәнімен беріледі.
Кир II-заңы
б,ша.
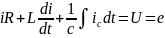
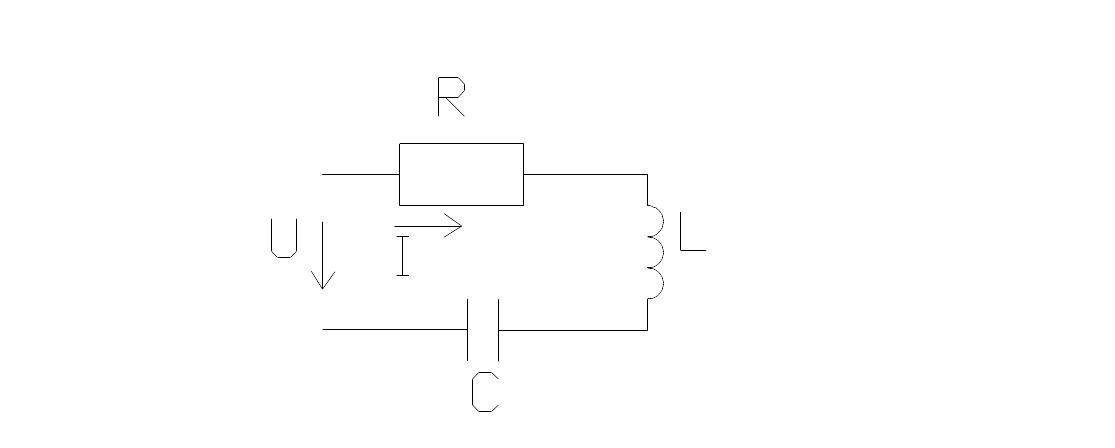
Қалыпты ток-ком кейін пайда болатын ток

Жалпы өтпелі ток ком кезі
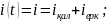
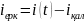 ;
;
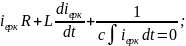
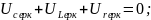
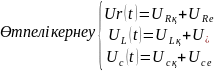

3 RL –тізбегінің өтпелі кезеңі. RL- тізбегінің қысқа тұйықталуы.
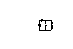
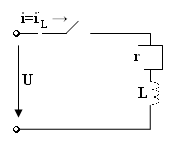 1.
Ком
дейнгі
i(0-)=E/(R+r)
2. Ком
кейнгі
Ik=0.
3. i(t)=iқ+iерк iерк=Ae-PT
Z(P)=r+PL=0
1.
Ком
дейнгі
i(0-)=E/(R+r)
2. Ком
кейнгі
Ik=0.
3. i(t)=iқ+iерк iерк=Ae-PT
Z(P)=r+PL=0
r+PL=0 P=-r/L
iерк=Ae-rt/L=E/(R+r) e-rt/L
i(t)=Ae-rt/L
i(0-)=i(0+)=i(0)=E/(r+r)
t=0 i(0)=A A=E/(R+r)
i(t)=E/(r+r) e-rt/L=iерк
τ=-1/P=L/τ
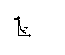

RL- өтпелі кезеңі.
![]()

1. Ком дейн i(0-)=E/R
2. Ком кейн ik=E/(R+r)
3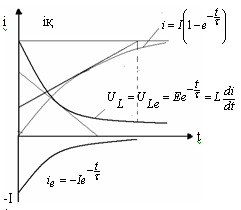 .
Ком
кезі i(t)=ik+iepk.
.
Ком
кезі i(t)=ik+iepk.
iepk=A e-rt/L=Ae-(k+τ)t/L
Z(P)=R+PL=0
P=-(R+r)/L
i(t)=E/(R+r)+A e-(r+R)t/L
i(0-)=i(0+)=i(0)=E/R
i(0)=E/R
t=0 E/(R+r)+A=E/R
A=E/R-E/(R+r)
i(t)=E/(R+r)+(E/R-E/(R+r)e-rt/L, A
UL(t)=LdiL(t)/dt

M: iL(t)=10+6e-600t
UL(t)=?
UL(t)=LdiL/dt=0.1(-3600e-600t)
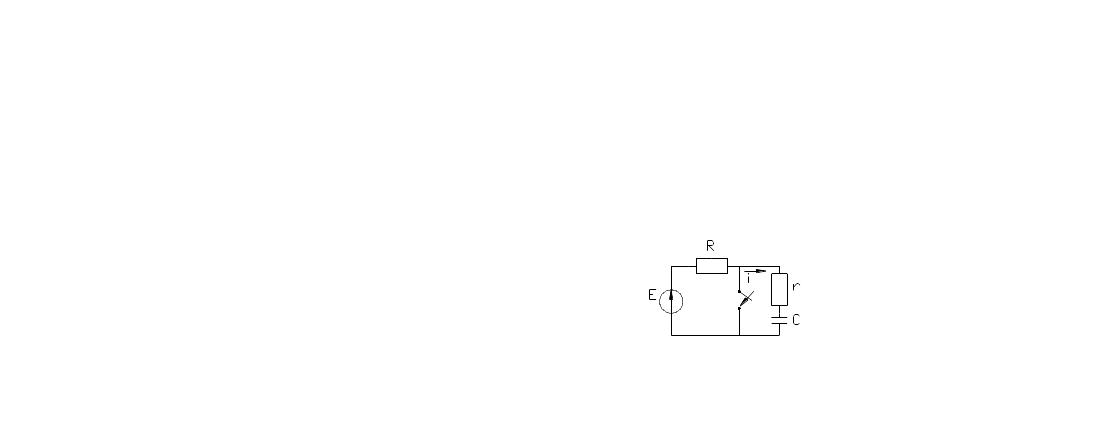
4. Rl тізбегін тұрақты кернеу көзімен қосу.
ri+Ldi/dt=U
i=iқал+iерк .
іқал=U/r.
i=iқал+iерк =U/r+Ae-t/τ,
τ=L/r.
t=0 0=U/r+A, A=-U/r.
uL=uLерк=Ldi/dt=Ue-t/τ
RL-ДІ ТҰРАҚТЫ Е –ҒА ҚОСУ
 ,
,


 кезде0=E/R+A
кезде0=E/R+A
A=-E/R
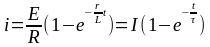 I=E/Rқалыптасқан
тоқ,
I=E/Rқалыптасқан
тоқ,
 уақыт
тұрақтысы
уақыт
тұрақтысы
Басты
мезгіл
 кезде
өздік индукцияның ЭҚК-і
кезде
өздік индукцияның ЭҚК-і
 ,
ол
көздің ЭҚК-ін толық өтемейді,
,
ол
көздің ЭҚК-ін толық өтемейді,
 .
.
5.Rc тізбегінің өтпелі кезеңі. Қысқа тұйықталуы.
Ком дейінгі
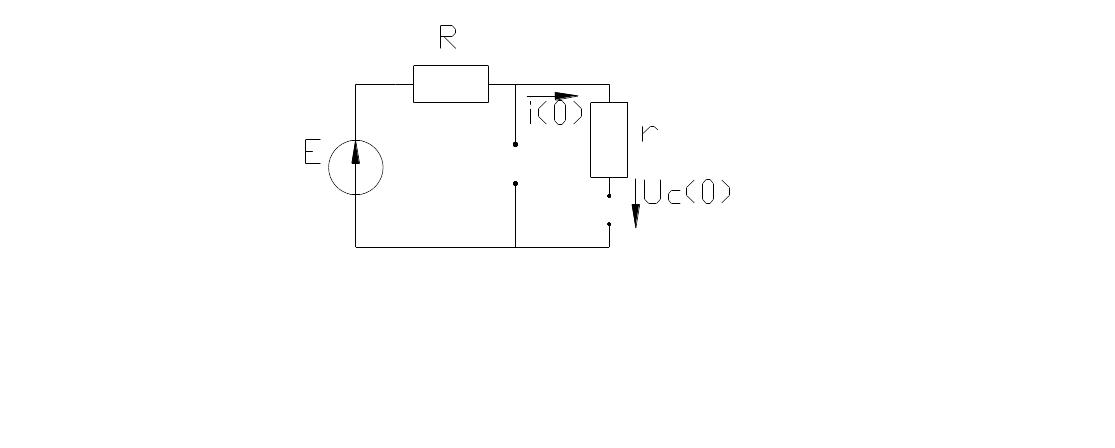
U(0)=0; Uc(0)=E;
![]()
iқ=0; Uсқ=0
Ком кезі
![]()
![]()
-jXc=1/jwc=(jw)=(p)=1/pc
Ком кезі Z(p)=r+1/pc=0
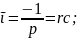 p=-1/rc(c-1)
p=-1/rc(c-1)
Uc(t)=Uc қ+Uc e
Uc e=Aept
Uc(t)=0+Aept
t=0
Uc(0)=A
ТБШ НБШ
Uc(0_)=Uc(0+)=Uc(0)=E
НБШ
Uc(0_)=Uc(0+)=Uc(0)=E
E=A Uc(t)=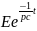
ic=c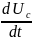
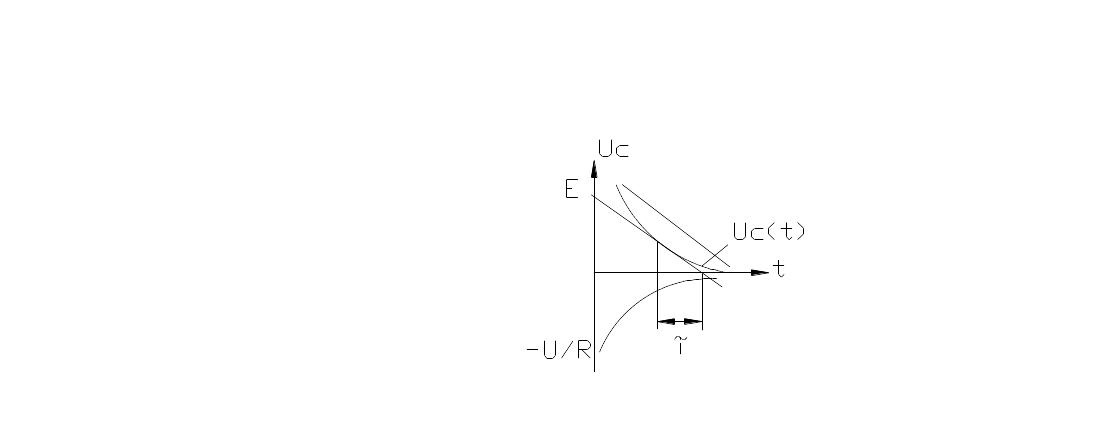
6. Rc тізбегін синусоидалы кернеу көзіне қосу
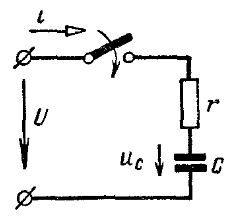
![]() кернеуіне
қосылсын.
кернеуіне
қосылсын.
![]()
3.
RLCp2+pL+R=0
P1,2=-R/2L±j√(R2/4L2-1/LC)![]()
![]() ,
,
![]()
![]()
UC=UCol+UCEPK=Um/zwc*sin(wt+ψ-ϕ-π/2)+Ae-t/τ![]()
Бастапқы
шарттардың
(t=0) беретіні:
![]() ,
осыдан
,
осыдан
![]() UC=Um/zwc*sin(wt+ψ-ϕ-π/2)+-U/zw*Csin(ψ-ϕ-π/2)*e-t/
UC=Um/zwc*sin(wt+ψ-ϕ-π/2)+-U/zw*Csin(ψ-ϕ-π/2)*e-t/![]()
Мұндағы
![]() – уақыт
тұрақтысы,
– уақыт
тұрақтысы,
![]() .
.
i=CdUC/dt=Um/R(cosϕ*sin(wt+ψ-ϕ)-sinϕ*sin(ψ-ϕ-π/2)e-t/τ
7. “Rlc” тізбегінің өтпелі кезеңі (тізбектей қосу)
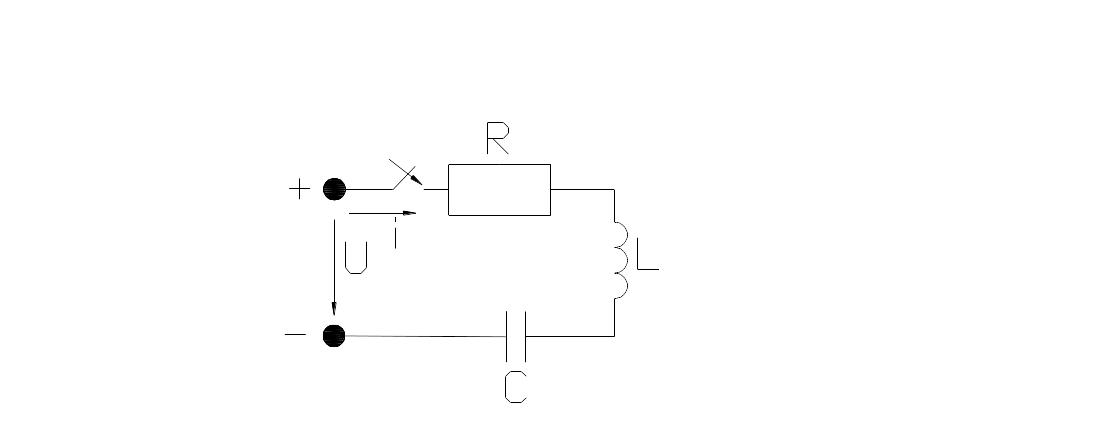
Кир II заңы б,а тізбектегі әр элементтің еркін кернеулері өзара теңеседі. Сондықтан тізбектей жалғанған контурда қорек көзі болмағандықтан өтпелі тоғымыз
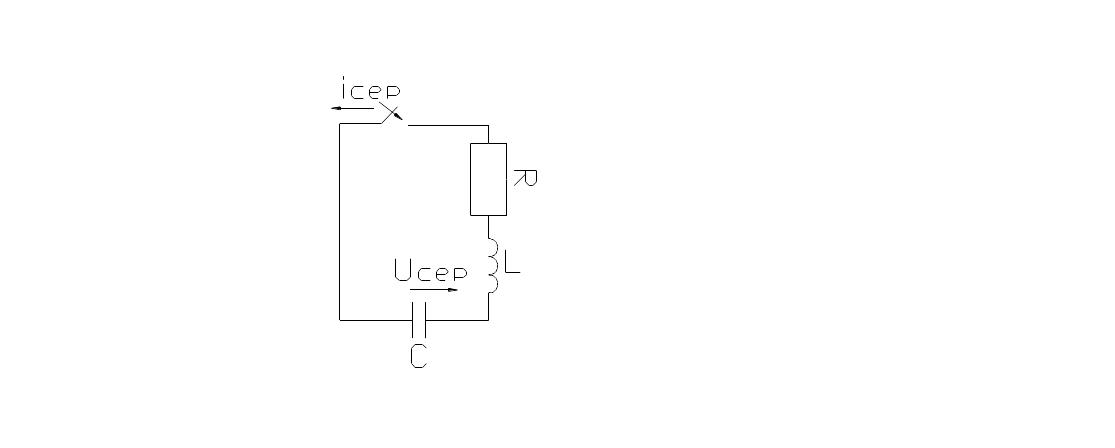
 ;
;
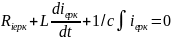 (1)
(1)
 (3)
(3)
(2) (1);
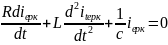 /L-бөлеміз
/L-бөлеміз
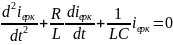 (3)
(3)
 (4)
/LC-бөлеміз
(4)
/LC-бөлеміз
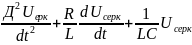 =0
(5)
=0
(5)
(3) пен
(5) б-ы ток пен кернеудің өзгеруі бірдей
теңдеу құрамыз
 -RLC-тізбегінің
сип-қ теңдеуі.
-RLC-тізбегінің
сип-қ теңдеуі.
Өтпелі кезеңді классикалық әдіспен есептеу реті.
1. Тәуелсіз бастапқы шартты анықтау.Тәулсі бастапқы шартты ком кейнгі тізбекке және ком заңдарын қолдана алады i2(0-), UC(0-).
2. Ком кейнгі Қалыптасқан режимді есептеу.
3. Кирхгофтың 1,2 заңы б/а ком кезіндегі теңдеун құру.
4. Ком кезіндегі сипаттамалық теңдеуін құру және түбірлеріне байланысты еркін құраушысын анықтау.
5.Анықталатын өтпелі ток пен кернеудің жалпы өрнексіз жазу.
6. Белгісіз шаманың мәндері б/а және оның бірінші реттік туындысы б/а интегралдау тұрақтысын анықтау.

1
1.![]()
![]()
4.
![]()
![]()
LdiL/dt-UC(0)=0
UC(0)=UCkal+UCepk
P1≠P2 UCepk=A1eP1t+A2eP2t
2. P1=P2=P
UCepk=(A1+A2t)ePt
Критикалық жағдай.
3. P1.2=-α±jw͢͢→UCepk=Ae-αtsin(wt±ϕ)
8)Rlc тізбегін тұрақты кернеу көзіне қосу.
2 сип-да
болады: апер-лық ж/е алгебралық.1)апер-лық;
Uс(0_)=U; i=0; iқал=0;
Uс=U+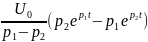 ;
;
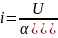 ;
;
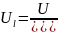 ;
2)алг-лық.
;
2)алг-лық.
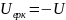 ;
Uс= Uсқал+Ucерк=U-
;
Uс= Uсқал+Ucерк=U-
 ;
Uқ=-ULерк-
;
Uқ=-ULерк-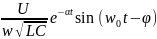 .
.
10. Сыйымдылықтың опериодикалық және тербелмелі разряды.
Егер контурлық кедергі критикалық кедергіден кіші болса сипаттамалық теңдеудің түбірі комплексті болса тербелмелінемесе периодты болады.
P1,2=-R/2L±j√(R2/4L2-1/LC)
R/2L= λ өшу коэф-і
W=√( R2/4L2-1/LC)=2π/Tepk – бұрыштық жиілік.
Терк –Контурдың еркін және қзіндік тербеліс периоды.
P1,2=α±jβ
UCерк=Ae-αtsin(wt+ψ)
UC(t)=Ae-αtsin(wt+ψ)
UC̍(t)=-αAe-αtsin(wt+ψ)+wAe-αtcos(wt+ψ)
t=0
{UC(0)=Asinψ
{UC̍(0)=-αAsinψ+wAcosψ
U=Asinψ
0=-αAsinψ+wAcosψ
Acosψ=Aαsinψ/w
w=Aαsinψ/Acosψ=αtgψ
tgψ=w/α ψ=arctgw/α
sinψ=w/√(L2+w2)
cosψ=α/√(α2+w2)
A=U/(w√(LC))
UC(t)=UCерк=UCTe-αtsin(wt+ϕ), B
i=iерк=Im e-αtsin(wt+ψ), A
Im=U/wL
Uct=ULm=U/(w√(LC))=U/sinψ
11) Операторлық түрдегі Ом ж\е кирхгоф заңдары.
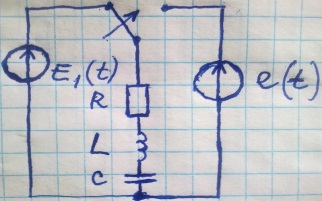
ТБШ:

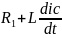 +Uc=e(t).
i(t)
+Uc=e(t).
i(t)
e(t)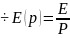
Ri(t)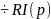

Uc(t)=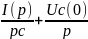 ,
,
 +Uc+
+Uc+ =Ep
=Ep
RI(p)+plI(p)-L (0)+
(0)+ .
I(p)(R+pl+
.
I(p)(R+pl+ =E(p)+L
=E(p)+L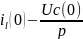 .
.
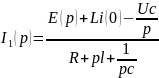
RLC тізбегі
жалғанған Операторлық Ом заңы. Z(p)=R+pl+ опер жалпы кедергі. Мұндағы L
опер жалпы кедергі. Мұндағы L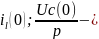 ішкі
н/е есептік ЭҚК
ішкі
н/е есептік ЭҚК
ТБШ бойынша
 ,
Uc(0)=0, онда ішкі ЭҚК операторлық сұлбада
есептелінбейді.
,
Uc(0)=0, онда ішкі ЭҚК операторлық сұлбада
есептелінбейді.
Ал Uc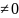 болған кезде ішкі ЭҚК енер сұлба
қарастырамыз.
болған кезде ішкі ЭҚК енер сұлба
қарастырамыз.
12,20,22)Дюамель
интегралын қолданып, өтпелі кезеңді
есептеу.Дюамель
интегралының көмегімен өтпелі кезеңді
есептеу реті. 1)тізбектің өтпелі ф-ясын
н/е сипаттамасын анықтау. тізбектің
өтпелі ф-ясы дегеніміз-тізбек реакциясының
I(t) бірлік ф-ясына әсер етуі. f(t)=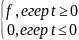 .
Егер тізбекті бірлік кернеу көзіне
қосса, онда кернеу б/а һu(t) өтпелі ф-ясын
ж/е өткізгіштік y(t) анықтауға болады.
Дюамель интегралының 4 формасы.
1)
.
Егер тізбекті бірлік кернеу көзіне
қосса, онда кернеу б/а һu(t) өтпелі ф-ясын
ж/е өткізгіштік y(t) анықтауға болады.
Дюамель интегралының 4 формасы.
1)
 .
2)
.
2) .
3)
.
3)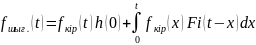 .
4)
.
4)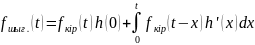 .
Ең
көп қолданылатын 1-ші форма. Мұндағы
.
Ең
көп қолданылатын 1-ші форма. Мұндағы
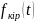 -кіріс
әсер етуші.
-кіріс
әсер етуші.
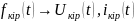 .
.
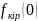 -кіріс
әсер етушінің басталу шамасы
-кіріс
әсер етушінің басталу шамасы
 әсер
етушінің туындысы dt. 2)іздестіріп
отырған токты н/е кернеуді интеграл
дюамельнің жазылуының бір түрінің
көмегімен анықтау.
i(t)=
әсер
етушінің туындысы dt. 2)іздестіріп
отырған токты н/е кернеуді интеграл
дюамельнің жазылуының бір түрінің
көмегімен анықтау.
i(t)=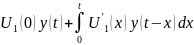 ,
U(t)=
,
U(t)=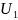 (0)hu(t)+
(0)hu(t)+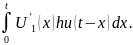
 кернеуі
аналитикалық кесінді ф-я түрінде
берілсін
кернеуі
аналитикалық кесінді ф-я түрінде
берілсін

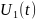 кернеуі
әртүрлі уақыт интервалында әр түрлі
теңдіктерге тең.
кернеуі
әртүрлі уақыт интервалында әр түрлі
теңдіктерге тең.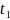 уақ-да
-секірісі
уақ-да
-секірісі
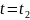 -
-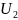 .
.

