
- •1 Вычислительные сети
- •1. Основные топологии физических связей. Полносвязная, ячеистая топологии, шина, звезда, кольцо, смешанные топологии.
- •2. Модель osi: протокол, стек протоколов, уровни (физический, канальный, сетевой, прикладной, уровень представления).
- •3. Стек протоколов tcp/ip: протоколы ip, tcp, udp, icmp.
- •2 Криптографические методы и средства обеспечения иб
- •4. Классические и новые задачи использования криптографии
- •1. Обеспечение конфиденциальности информации
- •2. Защита от навязывания ложных сообщений — имитозащита
- •3. Идентификация законных пользователей
- •4. Контроль целостности информации
- •5. Аутентификация информации
- •6. Системы тайного электронного голосования
- •7. Электронная жеребьевка
- •8. Защита документов (бумажных) и ценных бумаг от подделки
- •9. Иные задачи
- •7. Понятие электронно-цифровая подпись. Суть основных этапов реализации электронной цифровой подписи. Охарактеризовать выполнение цифровой подписи по алгоритму rsa и гост.
- •8.Охарактеризовать общую схему подписывания и проверки подписи с использованием хэш-функции. Кратко пояснить схему вычисления хэш-функции по гост р 34.11-94, по алгоритму sha.
- •9. Понятие pki. Классификация pki. Схемы реализации pki. Структура pkix.
- •1. Простая pki
- •2. Иерархическая pki
- •3. Сетевая pki
- •4. Архитектура кросс-сертифицированной корпоративной pki
- •5. Архитектура мостового уц
- •10. Законодательство рф в области криптографической защиты информации. (_коданев_а_)
- •3 Моделирование процессов и систем защиты информации
- •11. Модель Харрисона-Руззо-Ульмана. Анализ безопасности систем Харрисона-Руззо-Ульмана.
- •13. Модели мандатного доступа. Модель Белла и Лападула. Проблемы модели Белла и Лападула.
- •14. Модель Биба.
- •15. Вероятностная модель безопасности информационных потоков.
- •4 Инженерно-техническая защита информации
- •5 Технические средства защиты информации
- •6 Технические средства охраны
- •27. Системы контроля и управления доступом. Назначение и виды систем контроля и управления доступом. Системы телевизионного наблюдения. Видеокамеры и видеосервера.
- •Средства механической защиты
- •Средства технической охраны
- •7 Защита и обработка конфиденциальных документов
- •30. Сущность, особенности и основные определения конфиденциального делопроизводства. Виды тайн. Формы уязвимости информации. Задачи конфиденциальной информации.
- •8 Организационное обеспечение информационной безопасности
- •36. Аналитические исследования в системе мер по предупреждению утечки (секретной) конфиденциальной информации
- •37. Организация защиты информации при приеме в организации посетителей, командированных лиц и иностранных представителей.
- •38. Организационные мероприятия по допуску к секретной (конфиденциальной) информации
- •40. Организация и планирование контроля функционирования системы защиты информации.
- •41. Организационные мероприятия по доступу к конфиденциальной информации.
- •42. Организация защиты секретной (конфиденциальной) информации, обрабатываемой с использованием средств вычислительной техники.
- •43. Организация охраны территории, зданий, помещений и персонала.
- •9 Правовое обеспечение информационной безопасности
- •44. Формирование информационных ресурсов и их классификация.
- •45. Правовые основы защиты государственной, коммерческой и профессиональной тайны.
- •46. Правовые формы защиты интеллектуальной собственности.
- •Глава 69. Общие положения
- •Глава 75. Право на секрет производства (ноу-хау)
- •47. Система правовой ответственности за разглашение, утечку информации
- •Глава 28. Преступления в сфере компьютерной информации
- •48. Правовая защита от компьютерных преступлений
- •10 Организация и управление службой защиты информации на предприятии
- •54. Оргпроектирование деятельности сзи на предприятии (понятие, сущность и назначение). Методы оргпроектирования
- •55. Взаимосвязь элементов объекта и субъекта управления при планировании и проектировании работы сзи
- •56. Роль внутренней и внешней среды в управлении сзи (определение, характеристики). Их влияние на политику безопасности предприятия. Основные свойства управления сзи на предприятии.
- •11 Праграммно-аппаратная защита информации
- •1. Классические вирусы
- •1.1. Компилируемые вирусы
- •1.2. Интерпретируемые вирусы
- •1.2.1. Макровирусы
- •1.2.2. Скриптовые вирусы
- •2. Сетевые черви (worms)
- •3. Троянские кони (трояны)
- •4. Вредоносный мобильный код
- •5. Вредоносное по, реализующее смешанные способы атаки — Blended («смешанные») Attacks
- •6. Tracking cookies («следящие» куки)
- •7. Прочее вредоносное по
- •7.1. Бэкдуры (Backdoor)
- •12 Защита информационных процессов в компьютерных системах
- •63. Международные стандарты информационной безопасности. «Оранжевая книга». Европейские стандарты. Канадские стандарты. Общие критерии.
7. Электронная жеребьевка
Грубо говоря, подкидывание монеты «по сети». Допустим, надо решить, кто первый ходит в шахматной партии:
1. Алиса генерирует большое число X, шифрует его секретным ключом, получая Y.
2. Шифрограмма Y передается Бобу.
3. Алиса спрашивает Боба: четно/нечетно? Если Боб угадает четность числа, то ходит первым он.
4. Боб говорит Алисе свой ответ.
5. Алиса шлет Бобу свой секретный ключ и он расшифровывает Y, получая X.
8. Защита документов (бумажных) и ценных бумаг от подделки
Наиболее надежный современный метод пресечения их фальсифицирования. Основывается на том, что каждый материальный носитель уникален по микроструктуре (даже из 1 партии):
1. спец. сканером с высоким разрешением считываются особенности микроструктуры носителя;
2. формируется цифровой паспорт, вкл. содержание документа и инф. о микроструктуре носителя.
3. цифровой паспорт подписывается цифровой подписью изготовителя;
4. цифровой паспорт и соответствующая ему цифровая подпись записываются на носитель.
Проверка происходит путем сканирования носителя спецсканером, формирования его цифрового паспорта и проверки его цифровой подписи (открытые ключи публикуют в ряде изданий).
9. Иные задачи
Разработка новых криптосистем (в т.ч. квантовая криптография)
Совершенствование и разработка новых методов криптоанализа (квантовые компьютеры)
Разработка новых математических задач (наподобие проблемы факторизации и т.п.) для новых криптосистем
РАЗНОЕ
Основа ответа — книжка Беляева-Гольчевского «Введение в криптологию».
К разделу Идентификация законных пользователей
В книге написано «Идентификация законных пользователей», считаю некорректным использование слова «идентификация». Все говорит о том, что это аутентификация.
Слепая подпись
Полностью слепая подпись
Дана ситуация: Боб - нотариус. Алисе нужно, чтобы он подписал документ не имея никакого представления о его содержании. Боб только заверяет, что документ нотариально засвидетельствован в указанное время. Тогда они действуют по следующему алгоритму:
Алиса берёт документ и умножает его на случайное число. Оно называется маскирующим множителем.
Алиса отсылает документ Бобу
Боб подписывает документ и отсылает обратно
Алиса удаляет маскирующий множитель и получает свой документ с подписью.
Этот протокол работает только если функции подписи и умножения коммутативны.
Слепая подпись
Боб готовит n документов на каждом из которых написано некоторое уникальное слово (чем больше n, тем меньше у Боба шансов смошенничать).
Боб маскирует каждый документ уникальным маскирующим множителем и отправляет их Алисе.
Алиса получает все документы и случайным образом выбирает n-1 из них.
Алиса просит Боба выслать маскирующие множители для выбранных документов.
Боб делает это.
Алиса вскрывает n-1 документов и убеждается что они корректны.
Алиса подписывает оставшийся документ и отсылает Бобу.
Теперь у Боба есть подписанный Алисой документ с уникальным словом, которое Алиса не знает.
5. Охарактеризовать симметричные криптосистемы. Пояснить принципы работы современных блочных шифров (DES, ГОСТ 28147-89) для базовых режимов (ЕСВ, простая замена), режимов сцепления блоков (СВС), обратной связи по шифру (СFВ), по выходу (ОFВ), режимы гаммирования, гаммирования с обратной связью.
1.1. Симметричной системой шифрования - система, использующая единую ключевую информацию для процессов шифрования и расшифрования.
1.2. Определение блочного шифра (БШ). Криптографическое преобразование составляет основу любого БШ. При этом криптографическое преобразование (шифрование) переводит блок открытого текста в блок шифртекста той же длины. Обратное преобразование (дешифрование) переводит блок шифртекста в исходный блок открытого текста. Шифры, в которых размер данных блоков фиксирован, называются блочными. Сеть Фейстеля представляет собой разновидность итеративного БШ. Итеративность заключается в многократной, состоящей из нескольких циклов обработке одного блока открытого текста. При шифровании блок открытого текста разбивается на две равные части – правую и левую. На каждом цикле одна из частей подвергается преобразованию f и вспомогательного ключа кi ,полученного из исходного секретного ключа. Результат операции суммируется по мод. 2 с другой частью. Затем левая и правая части меняются местами. В последней итерации не выполняется перестановка. Дешифрование происходит по аналогичной схеме, но ключи при этом выбираются в обратном порядке. Конструкция Фейстеля применяется в госте и DES. Для симметричных БШ применяют различные схемы шифрования, или рабочие режимы шифрования.
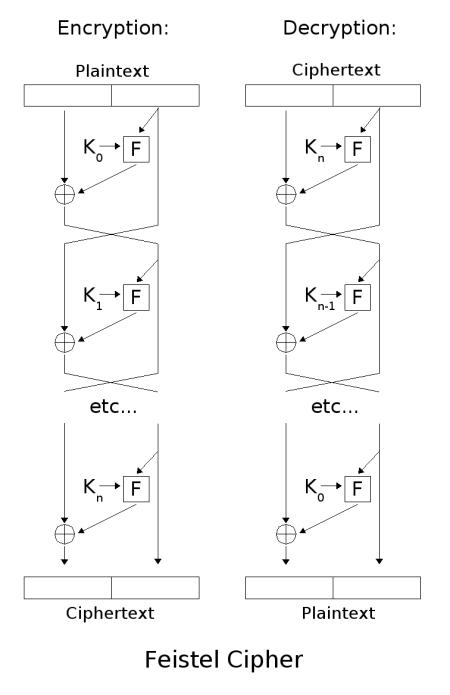
Каждый блок разбивается на два «подблока» (левый и правый, соотвественно).
Исходное заполнение правого блока записывается в левый блок на выходе.
Над правым блоком производится криптографическое преобразование с применением ключевых данных.
Левый (исходный) и правый (преобразованный) блоки складываются по модулю 2 в сумматоре по модулю 2.
Так повторяется несколько раз.
DES:
DES является классической сетью Фейcтеля с двумя ветвями. Данные шифруются 64-битными блоками, используя 56-битный ключ. Алгоритм преобразует за несколько раундов 64-битный вход в 64-битный выход.
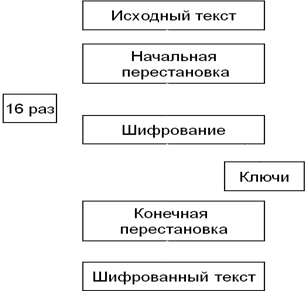
Начальная перестановка 64-битного исходного текста.
Использование сети Фейстеля 16 раундов.
Левая и правая половины выхода последней (16-й) итерации меняются местами.
Конечная перестановка результата, полученного на третьем этапе. Эта перестановка инверсна начальной перестановке.
В DES используется многократное чередование перемешивающих и рассеивающих преобразований, не управляемых ключом, и простых криптографических преобразований, выполняемых под управлением секретного ключа. Алгоритм DES преобразует входную информацию блоками по 64 бит. Двумя основными составными процедурами являются подстановка и перестановка, реализуемые, соответственно S- и P-блоками. Операции, выполняемые S-блоками и P-блоками, относятся к нелинейному типу, и именно они определяют надежность криптографического закрытия данных.
Функция P-блока заключается в перестановке входных битов без изменения количества нулевых и единичных битов.
Блоки S-типа воплощаются достаточно сложными схемами, реализующими заданные стандартом таблицы подстановок.
DES управляется 56-битовым ключом, из которого в каждом из 16 проходов используются выбираемые псевдослучайно 48 бит Ki.
Общая схема алгоритма DES состоит в следующем:
64-битовый блок открытого текста после начальной перестановки делится на две части по 32 бит каждая.
Левую и правую половины обозначим соответственно L и R. Затем выполняются 16 шифрующих итераций (раундов) вида:
Li = Ri – 1,Ri = Li F(Ri – 1, Ki),
где Ki — 48-битовый подключ, вырабатываемый по некоторым простым процедурам из 56-битового секретного ключа и используемый на i-ом раунде.
Сущность алгоритма DES раскрывается преобразованиями, которые выполняются для получения значения функции F(Ri-1, Ki) (рисунок). Процедура вычисления значения этой функции включает в себя: достаточно простую процедуру расширения 32-битового подблока в 48-битовый подблок R'; линейное преобразование, заключающееся в выполнении операции поразрядного суммирования по модулю два над подблоком R’ и подключом Ki; 8 операций подстановок типа 6х4 S1, S2, …, S8; операцию перестановки P.
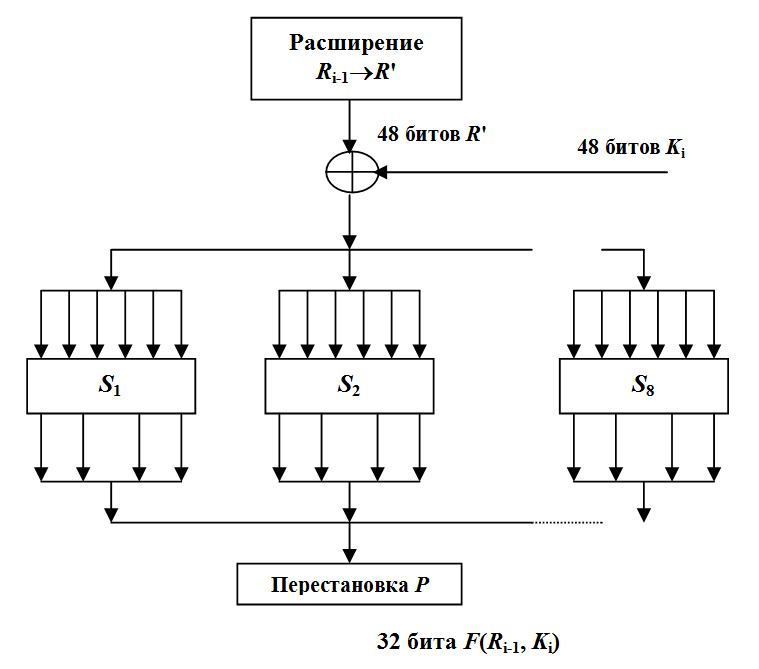
DES. Операция расширения
Операция расширения подблока R (R → R’) заключается в следующем. 32 бита подблока R разбиваются на восемь 4-битовых подблоков. К каждому 4-битовому подблоку с обоих сторон присоединяется по одному биту, в качестве которого берется ближайший крайний бит соседнего подблока (для первого 1-битового подблока соседним слева считается восьмой 4-битовый подблок; для 8-го 4-битового подблока соседним справа считается 1-й 4-битовый подблок).
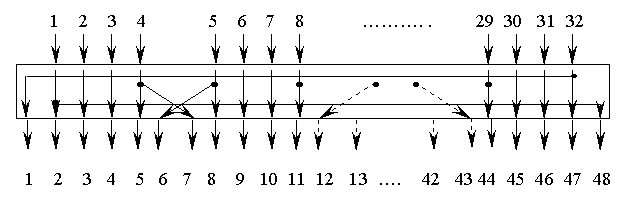
DES. Операция подстановки
После выполнения операции расширения R→R’ имеются восемь 6-битовых подблоков, над каждым из которых выполняется операция подстановки типа 6х4, дающая на выходе 4-битовое значение. Каждая из восьми подстановок задается таблицей из 4-х строк, которые представляют собой некоторые перестановки полного набора 4-битовых чисел {0, 1, 2, ..., 15}. Например, подстановка, S1 задается таблицей:
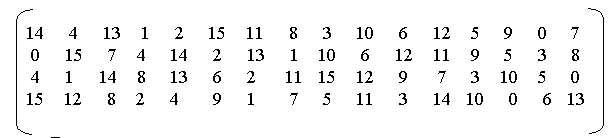
Выполнение операции подстановки состоит в следующем.
На основе 6-битового входного подблока формируются два двоичных вектора v1 и v2. Вектор v1 представляет собой 2-битовый подблок, содержащий 1-й и 6-й биты входного подблока, а вектор v2 содержит четыре средних бита.
Число, находящееся на пересечении строки с номером v1 и столбца с номером v2 берется в качестве выходного 4-битового подблока.
Всего используются 8 разных таблиц подстановки, аналогичных приведенной выше.
После выполнения восьми операций подстановки все 4-битовые выходные значения объединяются в 32-битовый подблок, над которым затем выполняется операция перестановки в соответствии с таблицами:
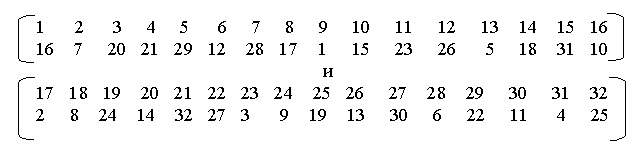
В этих таблицах верхняя строка обозначает порядковый номер позиции входных битов, а нижняя строка — номер позиции, в которую переставляются соответствующие биты.
В настоящее время основным недостатком DES является МАЛЕНЬКАЯ ДЛИНА КЛЮЧА. (решение - повторное применение шифрования с помощью DES с использованием нескольких ключей.)
Для алгоритма США DES различают следующие режимы:
1. Электронной
кодовой книги (ECB);
![]() ,
где E, D –
операции шифрования /расшифрования на
ключе k.
,
где E, D –
операции шифрования /расшифрования на
ключе k.
2. Сцепления блоков шифра (CBC) - каждый последующий блок открытого текста складывается с криптограммой предыдущего блока и результат шифруется.
3. Обратной связи по шифртексту (CFB) - i-й блок шифртекста формируется путем шифрования (i-1)-го блока шифртекста и суммированием с i-м блоком открытого текста
4. Обратной связи по выходу (OFB). Обратная связь по выходу отличается тем, что вместо (i-1)-го блока шифртекста поступает (s-1)-й блок преобразованной начальной последовательности.
ГОСТ
Этот стандарт криптографической защиты данных (СКЗД) представляет собой 64-битовый шифр, использующий 256-битовый секретный ключ, представленный в виде восьми 32-битовых подключей Qj, j = 0, 1, …, 7.
Процедуры шифрования и дешифрования соответствуют итеративной схеме Фейстеля, в которой функция F(R,K) задается:
операцией суммирования по модулю 232,
табличными подстановками, выполняемыми над 4-битовыми подблоками,
операцией циклического сдвига влево на 11 бит (далее обозначим эту операцию как “<<<11”), выполняемой над 32-битовым подблоком.
Табличные подстановки осуществляются следующим образом:
Подблок R представляется в виде конкатенации 4-битовых подблоков ri: R = r7| r6| r5| r4| r3| r2| r1| r0.
Над каждым подблоком ri выполняется операция подстановки, задаваемая таблицами S7, S6, …, S0. Каждая таблица представляет собой некоторую перестановку чисел {0, …, 15}, т.е. таблица S представляется упорядоченным набором 4-битовых чисел s0, s1, …, s15.
Обозначим операцию подстановки, выполняемую с помощью таблицы S над подблоком r через S (r). Эта операция заключается в замене значения r на значение sr, т.е. S (r) = sr.
Введем также функцию F’(R) = S7(r7) | S6(r6) |…| S0(r0).
Алгоритм шифрования:
1. ВХОД: 64-битовый блок исходного текста Т, представленный в виде конкатенации двух 32-битовых подблоков L и R: T = L | R.
2. Устанавливаем счетчик i = 1.
3. Сохраняем значение подблока R: V : = R.
4. Вычисляем номер выбираемого подключа j:
j = (i – 1) mod 8, если i < 25
j = (32 – i) mod 8, если i 25
5. Преобразуем подблок R:
R := (R + Qj) mod 232
R := F’(R)
R := R<<<11
R := R L
6. Преобразуем подблок L: L: = V.
7. Если i 32, то i := i + 1 и переходим к шагу 3.
8. ВЫХОД: 64-битовый блок шифртекста С = L | R.
Ниже представлена схема шифрующих преобразований ГОСТ 28147-89 и используются следующие обозначения: ki – ключевой элемент раунда, Xi – состояние процесса шифрования после i-того раунда, F (X, k) – функция шифрования, k – ключевой элемент раунда, S [] – функция подстановки, группами по 4 бита, <<<11 – операция циклического сдвига (вращения) 32-битового слова на 11 бит в сторону старших разрядов.
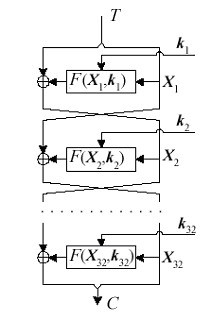
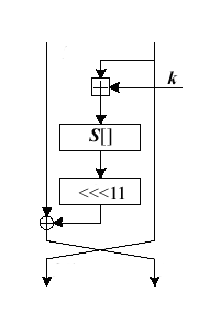
Сначала правая половина и i-ый подключ складываются по модулю 232. Затем результат делится на 8 частей по 4 бита и передается на блок подстановки, состоящий из 8 уникальных узлов замен (S-блоков). Каждый S-блок обрабатывает свою часть входного значения и преобразует 4 входных бита в 4 выходных. S-блок описывается как таблица состоящая из 8 строк и 16 столбцов по 4 бита вкаждой ячейке. Выходы всех S-блоков объединяются в 32-битное слово, которое затем Циклически сдвигается на 11 битов влево (P-блок). Наконец, с помощью XOR результат объединяется с левой половиной, в результате чего получается новая правая половина.
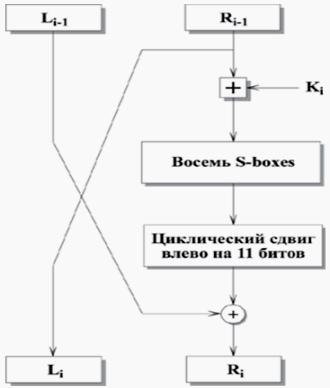
256-битный ключ разбивается на восемь 32-битных подключа. Алгоритм имеет 32 раунда, поэтому каждый подключ используется в четырех раундах по следующей схеме: 1-24 раунды (Q0..Q7), 25-32 раунды (Q7..Q0).
Считается, что стойкость алгоритма ГОСТ 28147-89 во многом определяется структурой S-блоков. Структура S-блоков в стандарте не определена.
ГОСТ 28147-89:
1.7) … таблицы блока подстановки являются секретными элементами и поставляются в установленном порядке…
Алгоритм может работать в следующих режимах:
Режим простой замены (ограничено стандартом) – ECB.
Режим гаммирования – OFB.
Режим гаммирования с обратной связь – CFB.
Режим выработки имитовставки.
Достоинства:
1. 256-битовый ключ. Атака, основанная на переборе возможных значений секретного ключа, полностью исключается.
2. Простое расписание использования ключа упрощает аппаратную реализацию стандарта.
3. 32 цикла шифрующих итераций обеспечивают высокую стойкость.
К недостаткам можно отнести:
Низкая скорость при программной реализации, что связано с использованием большого числа операций подстановки над 4-битовыми подблоками.
Основные проблемы ГОСТа связаны с неполнотой стандарта в части генерации ключей и таблиц замен. Доказано, что у ГОСТа существуют «слабые» ключи и таблицы замен, но в стандарте не описываются критерии выбора и отсева «слабых».(сильный ключ – ключ, у которого разница между количеством «1» и «0» не превышает трех).
3. Стандарт не специфицирует алгоритм генерации таблицы замен (S-блоков). С одной стороны, это может являться дополнительной секретной информацией (помимо ключа), а с другой, поднимает ряд проблем:
а) нельзя определить криптостойкость алгоритма, не зная заранее таблицы замен;
б) реализации алгоритма от различных производителей могут использовать разные таблицы замен и могут быть несовместимы между собой;
в) потенциальная возможность (отсутствие запрета в стандарте) использования таблиц замены, в которых узлы не являются перестановками, что может привести к критическому снижению стойкости шифра.
Различия между DES и ГОСТ:
DES использует гораздо более сложную процедуру создания подключей, чем ГОСТ 28147. В ГОСТ эта процедура очень проста. В DES применяется 56-битный ключ, а в ГОСТ 28147-89 – 256-битный. При выборе сильных S-блоков ГОСТ 28147-89 считается очень стойким. У S-блоков DES 6-битовые входы и 4-битовые выходы, а у S-блоков ГОСТ 28147-89 4-битовые входы и выходы. В обоих алгоритмах используется по восемь S-блоков, но размер S-блока ГОСТ 28147-89 существенно меньше размера S-блока DES.В DES применяются нерегулярные перестановки Р, в ГОСТ 28147-89 используется 11-битный циклический сдвиг влево. Перестановка DES увеличивает лавинный эффект. В ГОСТ 28147-89 изменение одного входного бита влияет на один S-блок одного раунда, который затем влияет на два S-блока следующего раунда, три S-блока следующего и т.д. В ГОСТ 28147-89 требуется 8 раундов прежде, чем изменение одного входного бита повлияет на каждый бит результата; DES для этого нужно только 5 раундов. В DES 16 раундов, в ГОСТ 28147 - 32 раунда, что делает его более стойким к дифференциальному и линейному криптоанализу.
Режимы шифрования:
ECB - Electronic Codebook (электрнонная кодовая книга) - каждый блок незашифрованного текста шифруется независимо от остальных блоков, с применением одного и того же ключа шифрования.
Типичные приложения: безопасная передача одиночных значений (например, криптографического ключа).

CBC - Chipher Block Chaining (сцепление блоков) - вход криптографического алгоритма является результатом применения операции XOR к следующему блоку незашифрованного текста и предыдущему блоку зашифрованного текста.
Типичное приложение: общая блокоориентированная передача, аутентификация.
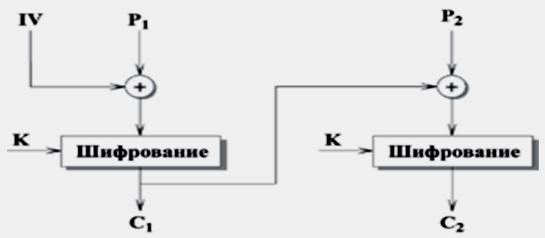
Для получения первого блока зашифрованного сообщения используется инициализационный вектор (IV), или синхропосылка (в терминах ГОСТ 28147-89), для которого выполняется операция XOR с первым блоком незашифрованного сообщения.
CFB - Chipher Feedback (обратная связь по шифру) - при каждом вызове алгоритма обрабатывается J битов входного значения. Предшествующий зашифрованный блок используется в качестве входа в алгоритм; к J битам выхода алгоритма и следующему незашифрованному блоку из J битов применяется операция XOR, результатом которой является следующий зашифрованный блок из J битов. Типичные приложения: потокоориентированная передача, аутентификация.

OFB - Output Feedback (режим по выходу) - аналогичен CFB, за исключением того, что на вход алгоритма при шифровании следующего блока подается результат шифрования предыдущего блока; только после этого выполняется операция XOR с очередными J битами незашифрованного текста.
Типичные приложения: потокоориентированная передача по зашумленному каналу (например, спутниковая связь).

Данный режим подобен режиму CFB. Разница заключается в том, что выход алгоритма в режиме OFB подается обратно в регистр, тогда как в режиме CFB в регистр подается результат применения операции XOR к незашифрованному блоку и результату алгоритма.
Основное преимущество режима OFB состоит в том, что если при передаче произошла ошибка, то она не распространяется на следующие зашифрованные блоки, и тем самым сохраняется возможность дешифрования последующих блоков.
Например, если появляется ошибочный бит в Сi, то это приведет только к невозможности дешифрования этого блока и получения Mi. Дальнейшая последовательность блоков будет расшифрована корректно.
Недостаток OFB в том, что он более уязвим к атакам модификации потока сообщений, чем CFB.
6. Охарактеризовать ассиметричные системы шифрования. Охарактеризовать секретные характеристики и выполнение шифрования (расшифрования) по алгоритмам RSA и ГОСТ. Сравнить симметричные и асимметричные схемы.
В 70-х годах У. Диффи ввел понятие односторонней функции с потайным входом. Это не просто вычислимая в одну сторону функция, обращение которой невозможно; она содержит потайной вход (trapdoor), который позволяет вычислять обратную функцию лицу, знающему секретный ключ. Сущность криптографии с открытым ключом (или двухключевой криптографии) заключается в том, что ключи, имеющиеся в криптосистеме, входят в нее парами и каждая пара удовлетворяет следующим двум свойствам:
текст, зашифрованный на одном ключе, может быть дешифрован на другом;
знание одного ключа не позволяет вычислить другой.
Поэтому один из ключей может быть опубликован. При опубликовании ключа шифрования и секретном ключе дешифрования получается система шифрования с открытым ключом. При опубликовании ключа дешифрования получается система цифровой подписи. С помощью цифровой подписи легко решается задача опознавания.
RSA основывается на том, что нахождение больших простых чисел в вычислительном отношении осуществляется легко, но разложение на множители произведения двух таких чисел практически невыполнимо. Доказано (теорема Рабина), что раскрытие шифра RSA эквивалентно такому разложению. Поэтому для любой длины ключа можно дать нижнюю оценку числа операций для раскрытия шифра, а с учетом производительности современных компьютеров оценить и необходимое на это время.
В настоящее время алгоритм RSA используется во многих стандартах, среди которых SSL, S-HHTP, S-MIME, S/WAN, STT и PCT.
Математические результаты, положенные в основу этого алгоритма.
Теорема 1. (Малая теорема Ферма.)
Если р простое число, то xp-1=1(modp) для любого х, простого относительно р, и xp = х (mod p) для любого х.
Определение. Функцией Эйлера j(n) называется число положительных целых, меньших n и простых относительно n.
Теорема 2. Если n=pq, (p и q - отличные друг от друга простые числа), то j(n)=(p-1)(q-1).
Теорема 3. Если n=pq, (p и q - отличные друг от друга простые числа) и х - простое относительно р и q, то xj(n) = 1 (mod n).
Следствие . Если n=pq, (p и q - отличные друг от друга простые числа) и е простое относительно j(n), то отображение Еe,n: x®xe (mod n)является взаимно однозначным на Zn.
Очевиден и тот факт, что если е - простое относительно j(n), то существует целое d, такое, что ed = 1 (mod j(n))
На этих математических фактах и основан популярный алгоритм RSA.
Пусть n=pq, где p и q - различные простые числа. Если e и d удовлетворяют уравнению (3), то отображения Еe,n и Еd,n являются инверсиями на Zn. Как Еe,n, так и Еd,n легко рассчитываются, когда известны e, d, p, q. Если известны e и n, но p и q неизвестны, то Еe,n представляет собой одностороннюю функцию; нахождение Еd,n по заданному n равносильно разложению n. Если p и q - достаточно большие простые, то разложение n практически не осуществимо. Это и заложено в основу системы шифрования RSA.
Пользователь i выбирает пару различных простых pi и qi и рассчитывает пару целых (ei, di), которые являются простыми относительно j(ni), где ni=pi qi . Справочная таблица содержит публичные ключи {(ei ,ni)}.
Предположим, что исходный текст x =(x0, x1, ..., xn-1), xÎZn , 0 £ i < n, сначала представлен по основанию ni : N = c0+ci ni+....
Пользователь i зашифровывает текст при передаче его пользователю j, применяя к n отображение Edi,ni : N ® Edi,ni n = n’.
Пользователь j производит дешифрование n’, применяя Eei,ni :N’ ® Eei,ni n’= Eei,ni Edi,ni n = n .
Очевидно, для того чтобы найти инверсию Edi,ni по отношению к Eei,ni, требуется знание множителей n=pi qi. Время выполнения наилучших из известных алгоритмов разложения при n=10100 на сегодняшний день выходит за пределы современных технологических возможностей.
Пример Зашифруем сообщение «САВ». Для простоты будем использовать маленькие числа (на практике применяются гораздо большие).
Выберем p=3 и q=11.
Определим n=3*11=33.
Найдем (p-1)(q-1)=20. В качестве d, взаимно простое с 20, например, d=3.
Выберем число е. В качестве такого числа может быть взято любое число, для которого удовлетворяется соотношение (е*3) (mod 20) = 1, например 7.
Представим шифруемое сообщение как последовательность целых чисел с помощью отображения: А®1, В®2, С®3. Тогда сообщение принимает вид (3,1,2). Зашифруем сообщение с помощью ключа {7,33}.
ШТ1 = (37) (mod 33) = 2187 (mod 33) = 9,
ШТ2 = (17) (mod 33) = 1 (mod 33) = 1,
ШТ3 = (27) (mod 33) = 128 (mod 33) = 29.
Расшифруем полученное зашифрованное сообщение (9,1,29) на основе закрытого ключа {3,33}:
ИТ1 = (93) (mod 33) = 729 (mod 33) = 3,
ИТ2= (13) (mod 33) = 1 (mod 33) = 1,
ИТ3 = (293) (mod 33) = 24389 (mod 33) = 2.
Итак, в реальных системах алгоритм RSA реализуется следующим образом: каждый пользователь выбирает два больших простых числа, и в соответствии с описанным выше алгоритмом выбирает два простых числа e и d. Как результат умножения первых двух чисел (p и q) устанавливается n.
{e,n} образует открытый ключ, а {d,n} - закрытый (хотя можно взять и наоборот).
Открытый ключ публикуется и доступен каждому, кто желает послать владельцу ключа сообщение, которое зашифровывается указанным алгоритмом. После шифрования, сообщение невозможно раскрыть с помощью открытого ключа. Владелец же закрытого ключа без труда может расшифровать принятое сообщение.
Стойкость:
Для того чтобы избежать выбора значения n, которое могло бы легко раскладываться на сомножители, на р и q должно быть наложено много дополнительных ограничений:
р и q должны друг от друга отличаться по длине только несколькими цифрами;
оба значения р и q должны быть от 1075 до 10100;
оба числа (р - 1) и (q - 1) должны содержать большой простой сомножитель;
НОД (p -1, q - 1) должен быть маленьким.
Электронная цифровая подпись.
Проблемы:
отказ от факта получения сообщения;
отказ от факта отправки сообщения;
выдача себя за другого пользователя с целью снятия с себя ответственности;
заявление, что получено некоторое сообщение от некоторого отправителя, хотя на самом деле оно не посылалось (или посылалось по другому адресу или с другим временем отправления);
заявление, что секретный ключ нарушителю передал смежный абонент сети связи, хотя на самом деле его передал сам заявитель и т.п.
Решение проблемы авторства может быть достигнуто лишь с использованием электронной цифровой подписи - средства, позволяющее на основе криптографических методов надежно установить авторство и подлинность документа.
С помощью цифровой подписи легко решается задача опознавания. Для этого опознающий посылает опознаваемому некий случайный текст и просит его подписать. Если подпись правильная, то опознаваемый является владельцем персонального ключа подписи. При этом опознающий не может получить какую-либо информацию о ключе подписи.
Выполнение цифровой подписи по RSA – то же что и шифрование, только шифруют на открытом ключе получателя сообщения.
ГОСТ
Формирование цифровой подписи:
Для
получения цифровой подписи под сообщением
![]() необходимо
выполнить следующие действия (шаги) по
алгоритму I.
необходимо
выполнить следующие действия (шаги) по
алгоритму I.
Шаг
1 - вычислить хэш-код сообщения
![]()
Шаг
2 - вычислить целое число а, двоичным
представлением которого является вектор
![]() ,
и определить
,
и определить
![]()
Если е = 0, то определить е = 1.
Шаг 3 - сгенерировать случайное (псевдослучайное) целое число k , удовлетворяющее неравенству
0 < k < q .
Шаг 4 - вычислить точку эллиптической кривой C = kP и определить
![]()
где
![]() -
x -координата
точки С .
Если r =
0, то вернуться к шагу 3.
-
x -координата
точки С .
Если r =
0, то вернуться к шагу 3.
Шаг 5 - вычислить значение
![]()
Если s = 0, то вернуться к шагу 3.
Шаг
6 - вычислить двоичные векторы
![]() и
и
![]() ,
соответствующие r и
s ,
и определить цифровую подпись
,
соответствующие r и
s ,
и определить цифровую подпись
![]() как
конкатенацию двух двоичных векторов.
как
конкатенацию двух двоичных векторов.
Исходными
данными этого процесса являются ключ
подписи d и
подписываемое сообщение М
, а выходным результатом
- цифровая подпись
![]() .
.
Схематическое представление процесса формирования цифровой подписи приведено на рисунке 2.
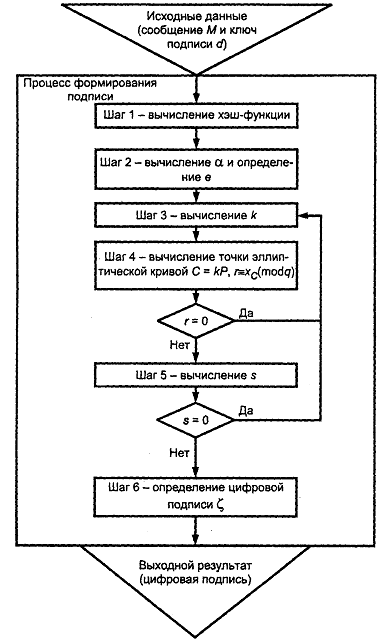
Рисунок 2 - Схема процесса формирования цифровой подписи
Проверка цифровой подписи
Для проверки цифровой подписи , под полученным сообщением М необходимо выполнить следующие действия (шаги) по алгоритму II.
Шаг 1 - по полученной подписи вычислить целые числа r и s . Если выполнены неравенства 0 < r < q, 0 < s < q , то перейти к следующему шагу. В противном случае подпись неверна.
Шаг 2 - вычислить хэш-код полученного сообщения М
![]()
Шаг
3 - вычислить целое число
![]() ,
двоичным представлением которого
является вектор
,
двоичным представлением которого
является вектор
![]() ,
и определить
,
и определить
![]()
Если е = 0, то определить е = 1.
Шаг 4 - вычислить значение
![]()
Шаг 5 - вычислить значения
![]()
Шаг
6 - вычислить точку эллиптической кривой
![]() и
определить
и
определить
![]()
где
![]() -
x -координата
точки С .
-
x -координата
точки С .
Шаг 7 - если выполнено равенство R = r , то подпись принимается, в противном случае, подпись неверна.
Исходными
данными этого процесса являются
подписанное сообщение М,
цифровая подпись
![]() ,
и ключ проверки Q,
а выходным результатом - свидетельство
о достоверности или ошибочности данной
подписи.
,
и ключ проверки Q,
а выходным результатом - свидетельство
о достоверности или ошибочности данной
подписи.
Схематическое представление процесса проверки цифровой подписи приведено на рисунке 3.
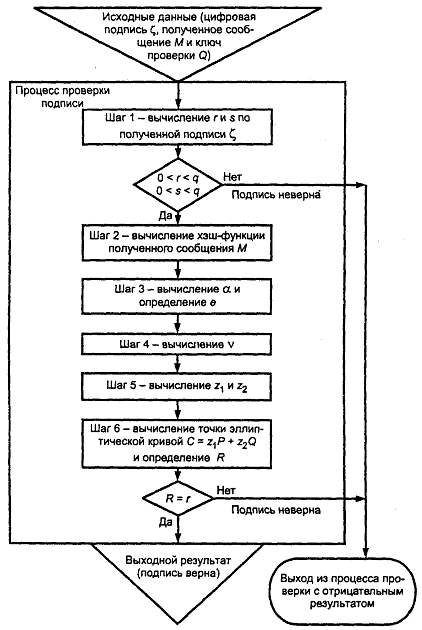
Рисунок 3 - Схема процесса проверки цифровой подписи
Симметричным называют шифр, в котором для шифрования и дешифрования используется один и тот же ключ (или разные ключи, которые связаны между собой в математическом смысле, то есть один ключ легко вычисляется из другого фактически, такая ситуация все равно сводится к одному ключу). Поскольку единственный ключ полностью обеспечивает секретность шифра, симметричные шифры называют иногда шифрами «с секретным ключом» или «с разделяемым ключом».
В противоположность этому, в асимметричных шифрах используется пара ключей, между которыми существует математическая связь, однако вычислить один ключ по другому крайне трудно. Благодаря этому обстоятельству мы можем хранить в тайне лишь один из ключей, сделав второй публично доступным.
